ΔT(M)=Te(M)−Ts(M)
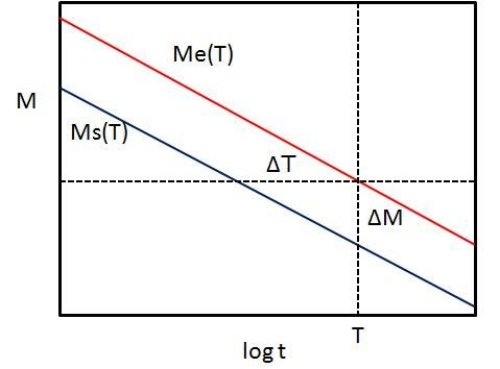
である。等時線上ではある時刻TでのRC開始質量 Ms(T)とRC終了質量Me(T)が与えられ、RCの質量幅は、
ΔM(T)=Me(T)−Ms(T)
では、ΔT(M)とΔM(T)の関係はどうなのだろう?
右の図を見ると、
| ΔT(Me)=ΔM | dTs | =ΔM | ( | Ts | ) | dlogTs | |
| dM | M | dlogMs |
| Filter | U | B | V | R | I | J | H | K | |
|---|---|---|---|---|---|---|---|---|---|
| λeff (Å) | 3641.89 | 4460.62 | 5501.70 | 6557.09 | 8036.57 | 12314.46 | 16369.53 | 21937.19 | |
| ωeff (Å) | 640 | 920 | 920 | 1640 | 1260 | 2000 | 2325 | 3200 | |
| Aλ/AV | 1.54892 | 1.29719 | 1.00600 | 0.81512 | 0.60329 | 0.29100 | 0.18372 | 0.11471 |
| Filter | UX | BX | B | V | R | I | J | H | K | L | L' | M | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λeff (Å) | 3627.36 | 4478.30 | 4459.58 | 5500.02 | 6498.73 | 8010.27 | 12269.18 | 16324.85 | 21874.56 | 34518.32 | 38017.59 | 47174.98 | |
| ωeff (Å) | 580 | 920 | 920 | 920 | 1600 | 1240 | 2050 | 2375 | 3200 | 4750 | 4600 | 4000 | |
| Aλ/Av | 1.55468 | 1.29213 | 1.29749 | 1.00640 | 0.82378 | 0.60708 | 0.29276 | 0.18452 | 0.11524 | 0.01791 | 0.00000 | 0.00000 | |
| Aλ/Av | 1.55468 | 1.29213 | 1.29749 | 1.00640 | 0.82378 | 0.60708 | 0.29276 | 0.18452 | 0.11524 | 0.01791 | 0.00000 | 0.00000 |
| Filter | V | J | H | K | L | L' | M | (M) | |
|---|---|---|---|---|---|---|---|---|---|
| λeff (μm) | 0.545 | 1.22 | 1.63 | 2.19 | 3.45 | 3.80 | 4.75 | ||
| Fλ(10-11W m-2 μm-1) | 3590 | 312 | 114 | 39.4 | 6.99 | 4.83 | 2.04 | 1.97 | |
| Fν(Jy) | 3600 | 1570 | 1020 | 636 | 281 | 235 | 154 | 152 |
| Filter | B | V | R | I | J | H | K | L | L' | M | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| λeff (μm) | 0.438 | 0.545 | 0.641 | 0.798 | 1.22 | 1.63 | 2.19 | 3.45 | 3.80 | 4.8 | |
| Fo(ν)/Jy | 4063 | 3636 | 3064 | 2416 | 1589 | 1021 | 640 | 285 | 238 | 170 |
Z=0.019 Z=0.008 Z=0.004 Z=0.002 Z=0.0004 Z=0.0002 年齢(Gyr) |
|
イメージが湧くようにRCの寿命を考える。RC開始TsとRC終了Teは初期
質量Mの関数なので、Ts(M)、Te(M)とする。RC寿命は、 ΔT(M)=Te(M)−Ts(M) である。等時線上ではある時刻TでのRC開始質量 Ms(T)とRC終了質量Me(T)が与えられ、RCの質量幅は、 ΔM(T)=Me(T)−Ms(T) では、ΔT(M)とΔM(T)の関係はどうなのだろう? 右の図を見ると、
|

|
メタル量 0.019 0.008 0.004 0.002 0.0004 0.0002 |

|
| rs | ) | 2 | ||
| re |