A - E = 0.035 P km/s
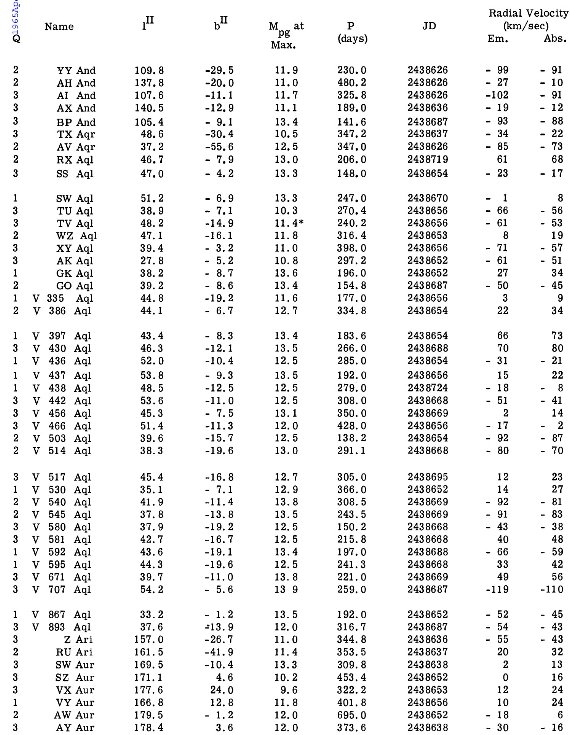
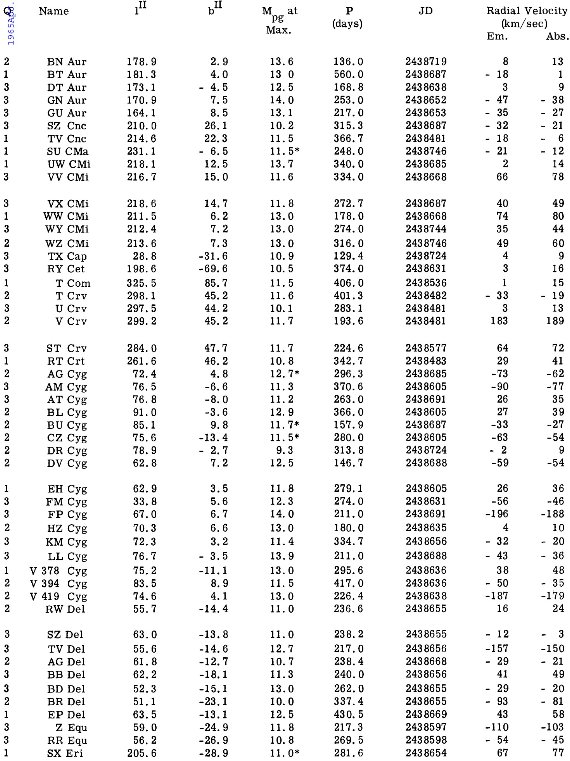
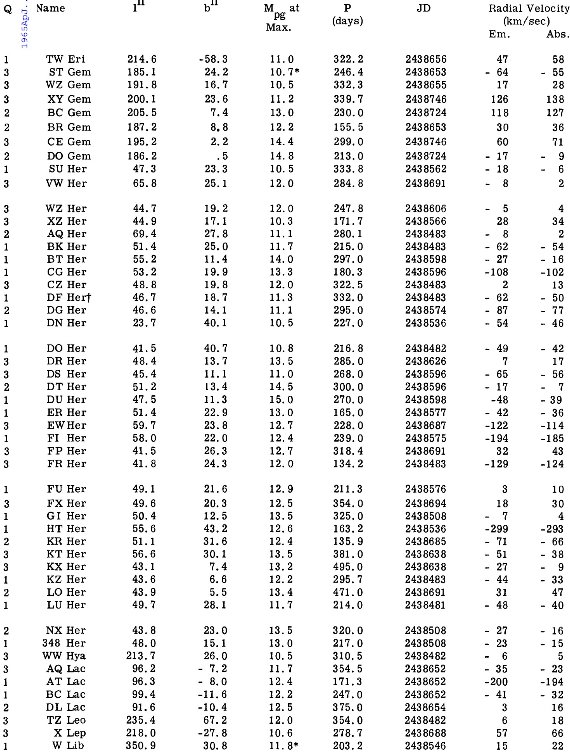
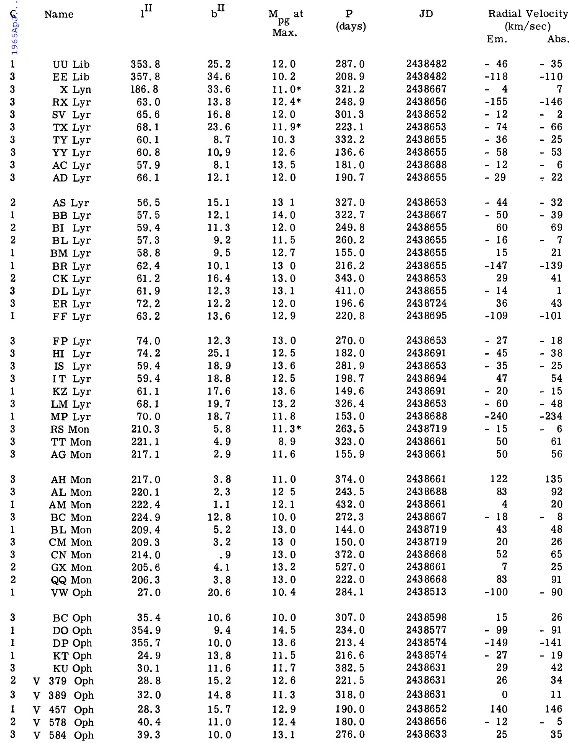
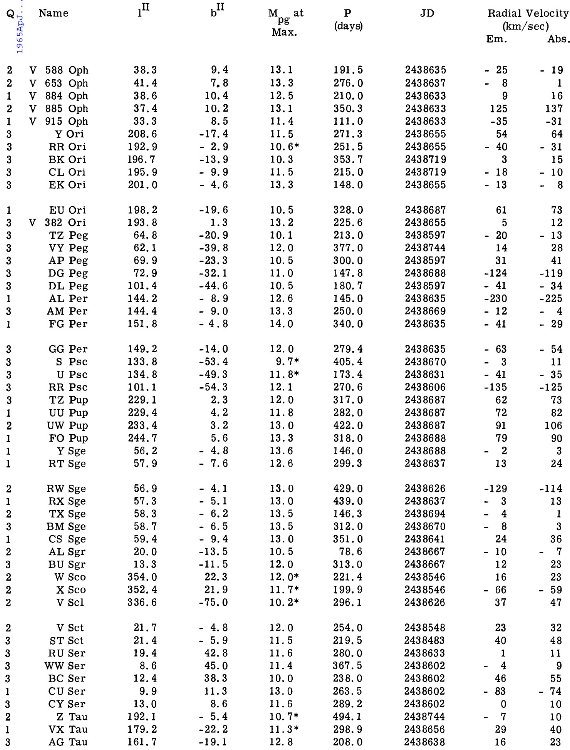
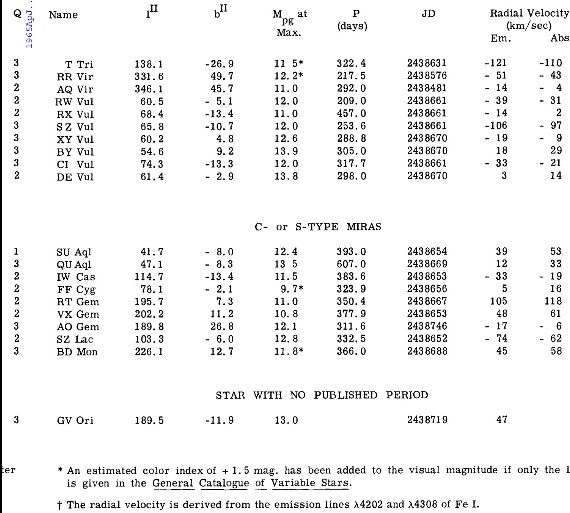
輝線速度及びそこから導いた吸収線速度は表3に示す。
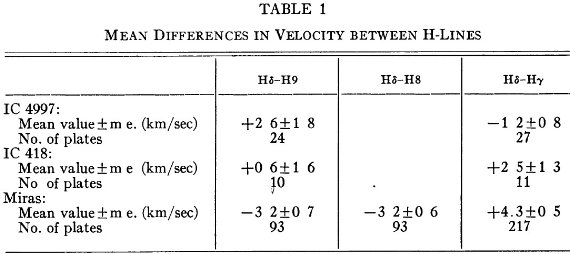
表1.水素線間の速度差
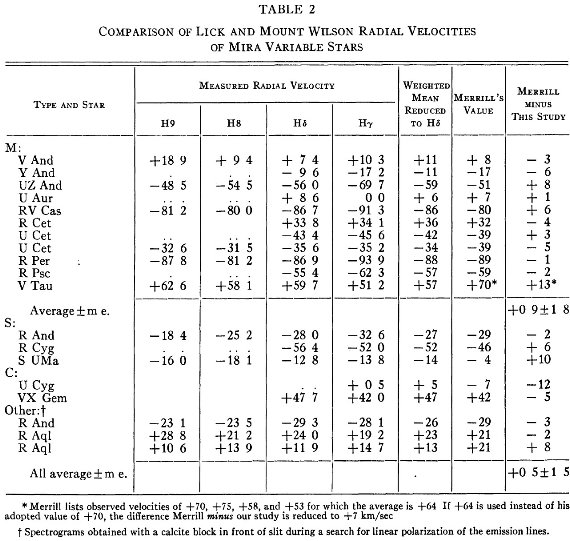
表2.リックとウィルソン山天文台のミラ型星視線速度測定の差
| リック天文台 120 インチクーデ分光器による 270 個のミラ型星の観測から これまで報告のなかった視線速度を初めて与えた。多くは mpg = 10 - 15 mag である。これらの結果を Merrill や Feast の結果に足して、 ミラ型星の運動を論じた。距離は Osvald, Risley の絶対等級を用いて決めた。 減光は指数関数型減光層モデルを使用した。 | 減光率には 1.5, 2.0, 2.5 p.g.mag/kpc の3種類を試した。オールト定数 A = 15 km/s/kpc が P < 350 d のミラ型星に対して得られた。P > 350 d のミラに対しては、もっと大きい A = 25 km/s/kpc が得られた。銀河 中心の周りの回転速度は銀河面から上がるにつれ低下して行く。この低下は 楕円体仮説に基づいて説明される。それによって Vθ, A, Rmax, Vθ が極大となる銀河中心距離の z-依存表現が 得られた。 |
|
Merrill および
Feast (1963)
に従って、吸収線速度と輝線速度の間に次の差を仮定する。 A - E = 0.035 P km/s 輝線速度及びそこから導いた吸収線速度は表3に示す。  表1.水素線間の速度差 |
 表2.リックとウィルソン山天文台のミラ型星視線速度測定の差 |
 |
 |
 |
 |
 |
 |
|
絶対等級 Osvalds, Risley 1961 から、 Mpg = -0.2 (P < 140) Mpg = -13.4 + 5.4 logP (P > 140) 星間減光 星間減光には Parenago 1945 による層分布モデルを用いた。
我々は β = 150 pc を採用した。これは Zonn 1956 の 125 pc と最近の Abt, Golson 1962 の値 187 pc の中間である。a0 = 1.5, 2.0, 2.5 mag/kpc の3種類を試した。 距離の計算 我々のサンプルに Merrill, Feast (1963) のサンプルも加え、距離を計算した。銀河面上の分布を a0 = 2 mag/kpc について図1に示した。 図1.ミラ型星の分布。(a) P = [140, 240] (b) P = [240, 340] (c) P = [340 700] 黒丸は |z| < 1 kpc. 白丸は |z| > 1 kpc. |
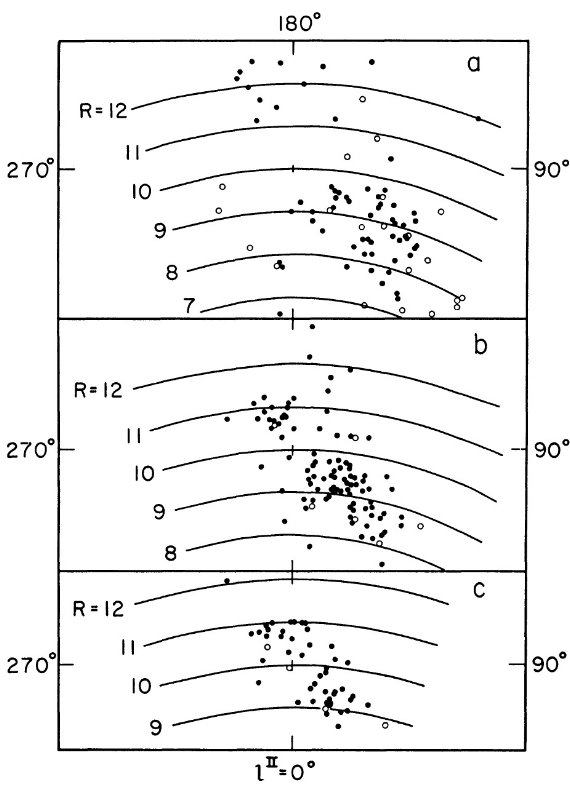 |
|
表4=グループ分け 第4章サンプルの視線速度を解析した。太陽運動はMerrill, Feast と同じ 以下の値を使用した。 u0 = 10.11 (l = 0, b = 0 方向) v0 = 9.63 (l = 90, b = 0 方向), w0 = 6.25 (b = 90 方向), ( u の方向が逆なので、気づくまで悩んだ。) 周期 P と銀河中心距離 R, 銀河面距離 z で表4のようにサンプル星を13に分けた。 VR, Vθ, Vz グループ毎に平均運動 VR, Vθ, Vz を次の式の最少二乗解として求める。 Vr'+Vc sin l cos b = VR cos α cos b + Vθ sin α cos b + Vz sin b ここに、sin α = (Ro/R) sin l, Vc = LSR の円周速度。Ro = 10 kpc. VR = -(dR/dt) であることに注意。 速度散布度 σR, σθ, σz を最小二乗法から求める式は、 σR2(cosαcosb)2 + σθ(sinαcosb)2 σz2(sinb)2 = (ΔVr')2 ΔVr'=Vr'+Vc sinlcosb-VRcosαcosb- Vθsinαcos b-Vzsinb 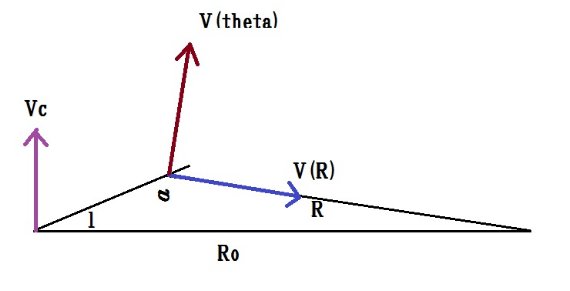 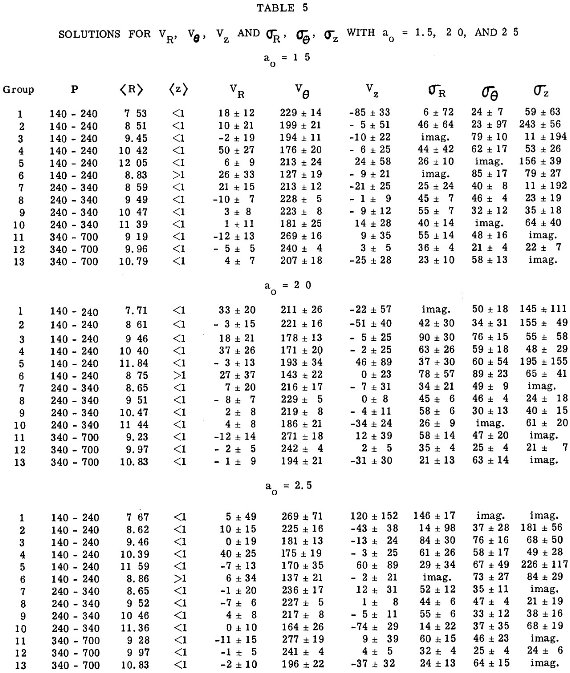 表5.VR, Vθ, Vz, σR, σθ, σz の解。 |
この解を表5に示す。サンプルの不完全さのため、ある場合には分散が負になった。
それらは "imag" とした。幾つかの場合では VR と Vθ
は散布度と同じくらいかより大きい。そのような場合、もし VR =
Vθ = 0 とすると、Feast 1963 が示すように散布度はもっと
大きくなる。彼のサンプル星は我々より一様な分布を示し、彼の σR
と σz はより精度が高い。 回転曲線の勾配 A と曲率 α 回転曲線の勾配 A と曲率 α は各グループに対し、次の式の最少二乗 解で決まる。 Vr'+Vc sin l cos b = U cos α cos b + V sin α cos b + W sin b -2 A (R - R0) sin l cos b - 2 α (R - R0) 2 sin l sin b ここに、U, V, W は銀河系座標系グループ速度の R = Ro における直交成分である。
得られた結果を表6に示す。 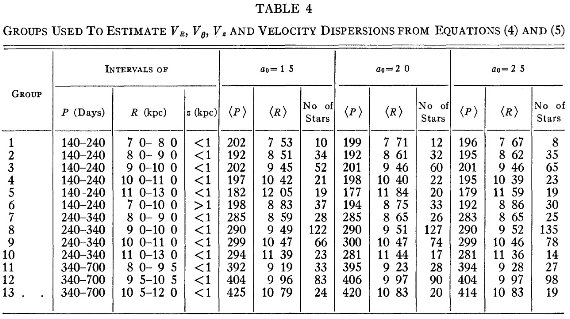 表4.VR, Vθ, Vz と速度散布度を 評価する際のグループ分け。 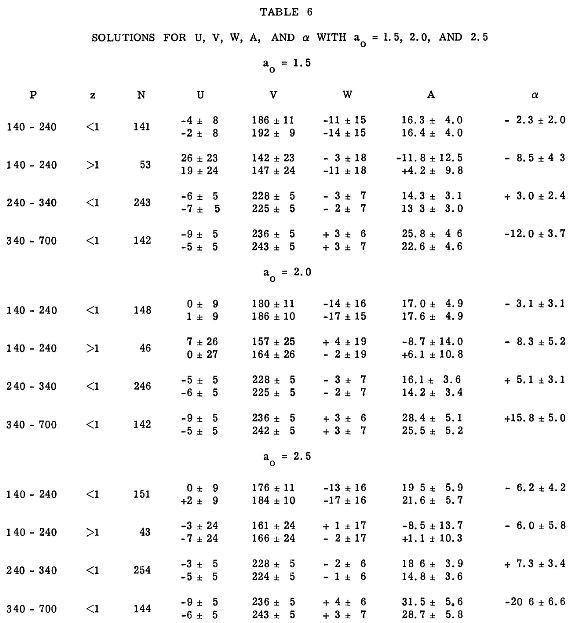 表6.U, V, W, A, α の解 |
|
Aはどのくらい本当か? 我々の得た結果は図2、3にまとめて示されている。 Merrill (1941), Feast (1963) が発見したように V は周期 P と共に増加していく。V の値自体は α 項 を入れてもあまり変わらない。U, W はどの場合でも十分に小さい。A の値は |z| < 1 kpc の星に対してはエラーより有意に大きい。Feast はミラの微分 回転を定めようと試みたが、我々のエラーを Feast のそれと較べると、A を 信頼できる精度で求めるには太陽距離 1 kpc 以上の天体の観測が必要である。 最初の2グループ(最短周期)に対する A = 15 は B-型星(Rubin, Burley 1964), セファイド (Kraft, Schmidt 1963) の値と驚くほど近い。しかし、 P = [340, 700] に対する値は、Vc = 250 km/s, Ro = 10 kpc からの可能最高値 18 を越える。このグループに対する距離を過小評価しているのかも知れない。 第2グループと第3グループの間で A の値がジャンプする。これは P > 350 ミラのエラーが大きいことを意味するのかも知れない。表7を見ると、 Feast のデータも同じジャンプを示している。太陽距離 1 kpc 以上のデータは 主にリック天文台で撮られ、銀経分布に偏りがある。 α について α のエラーは大きいので、その値には注意が必要である。 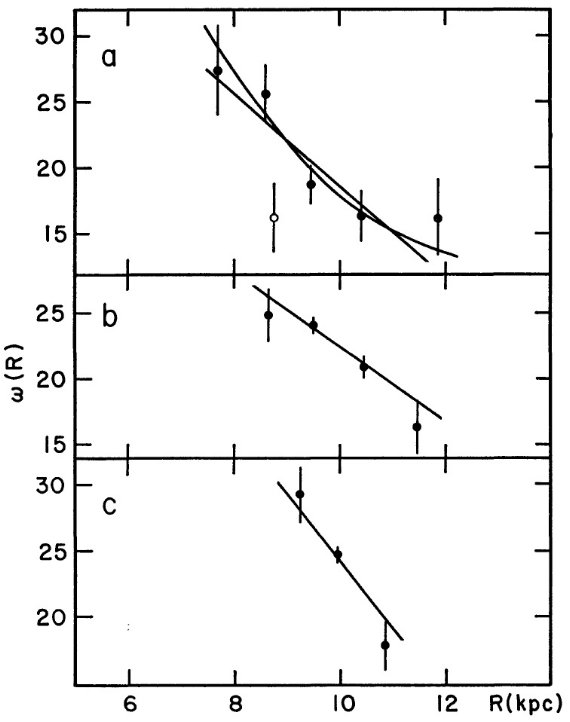 図2.ω(R) = V(θ)/R の R 変化。a0 = 2.0 mag/kpc 仮定。 (a): P = [140, 240] (b): P = [240, 340] (c): P = [340, 700] 直線は表6の α = 0 解。(a) の曲線= A, α を入れた解。白丸= |z| > 1 の星に対する V(θ) |
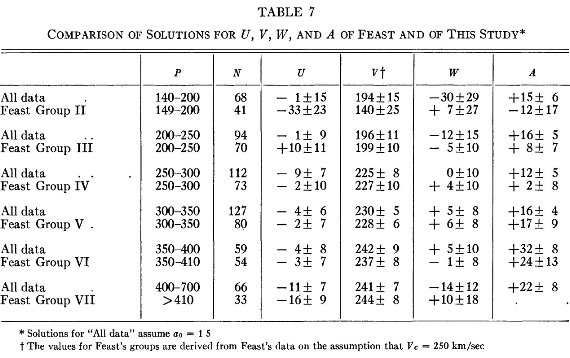 表7.U, V, W, A の比較。Feast の結果も載せた。 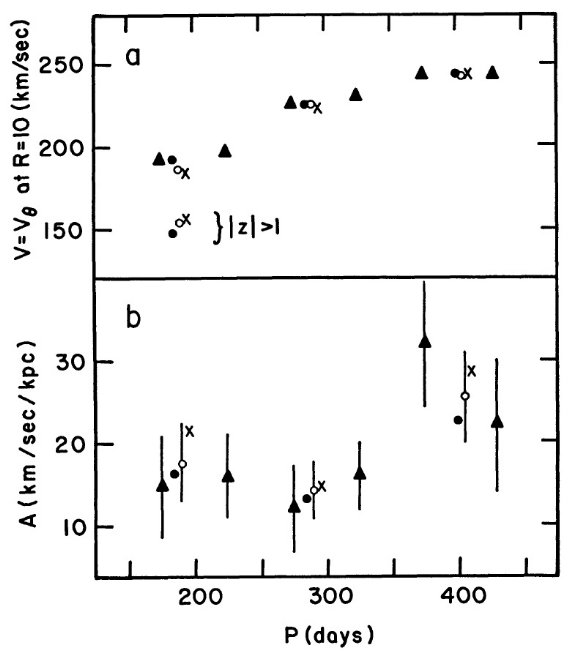 図3.(a): V の周期 P による変化。黒丸は a0 = 1.5 mag/kpc, 白丸は a0 = 2.0 mag/kpc, バツは a0 = 2.5 mag/kpc。 三角は表7の小さい周期間隔、a0 = 1.5 mag/kpc に対する V. (b): A の P による変化。 |
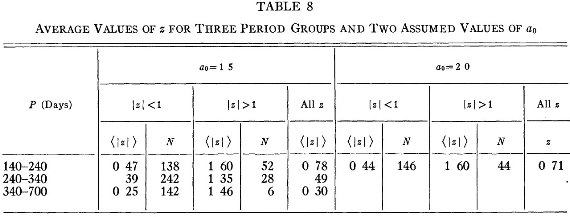 図8.3つの周期グループと2種の α0 に対する z 平均値 |
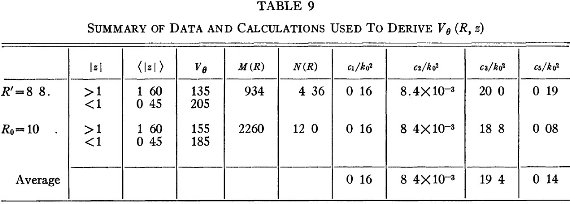 図9.Vθ(R, z) を導くのに使ったデータ |