|
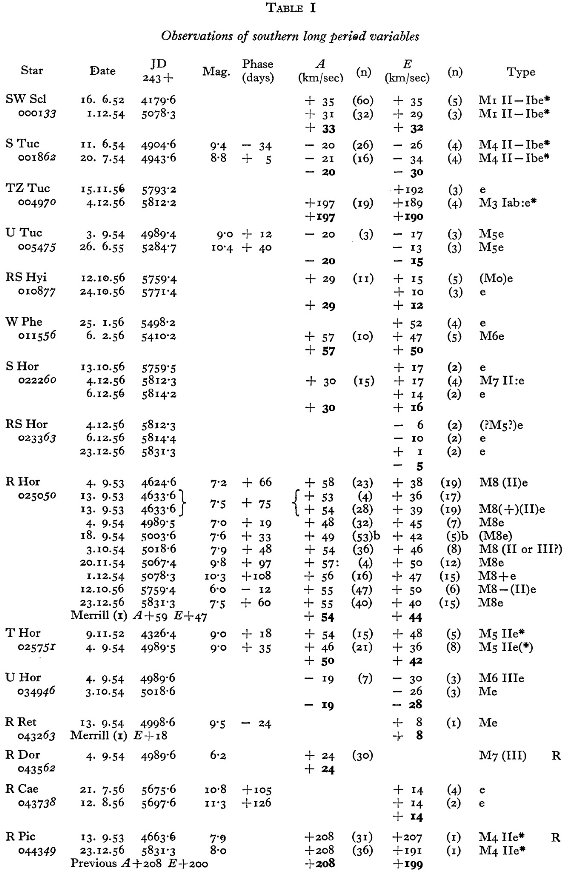
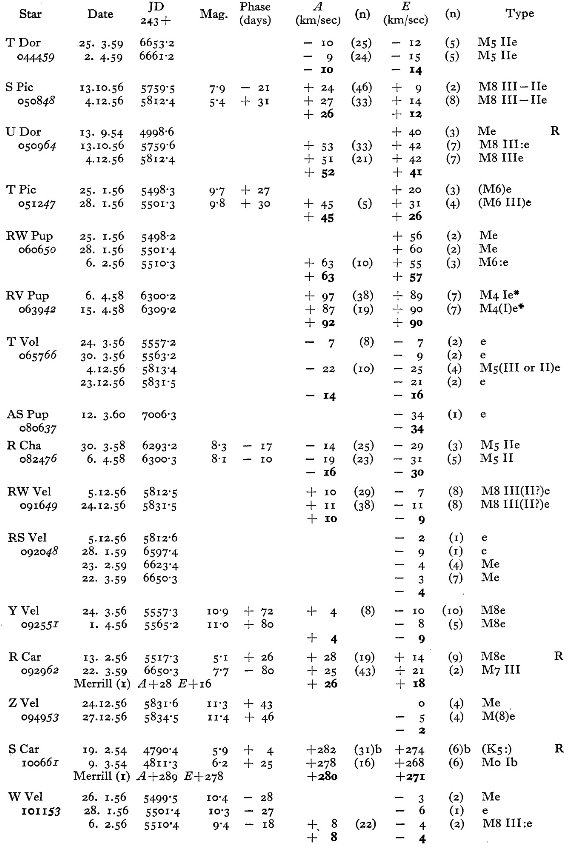
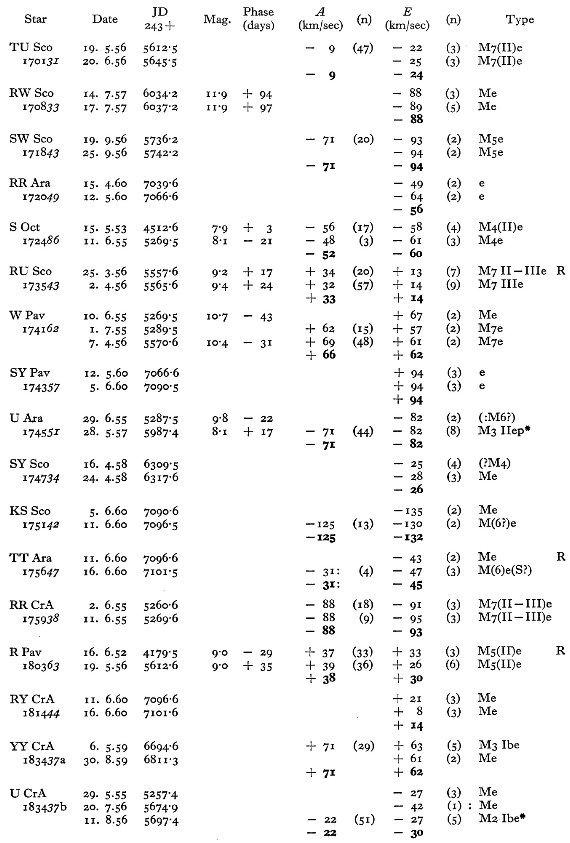
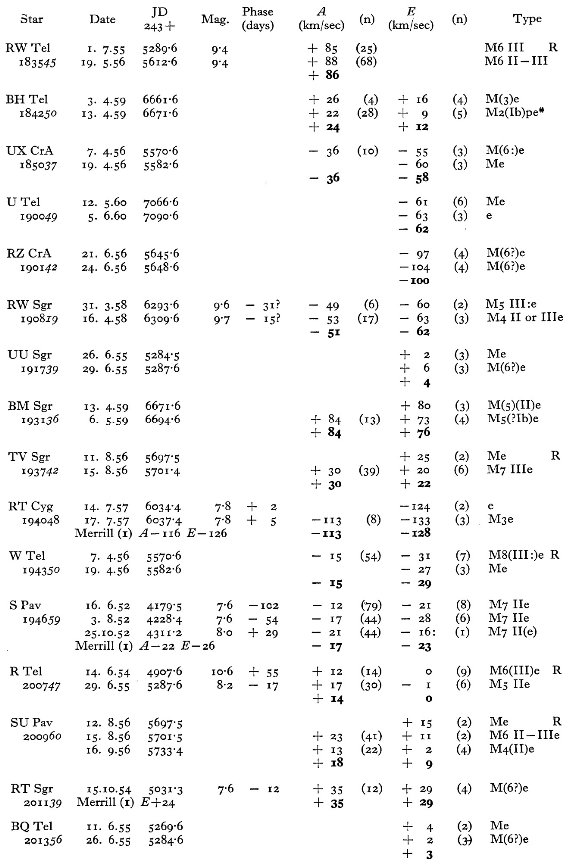
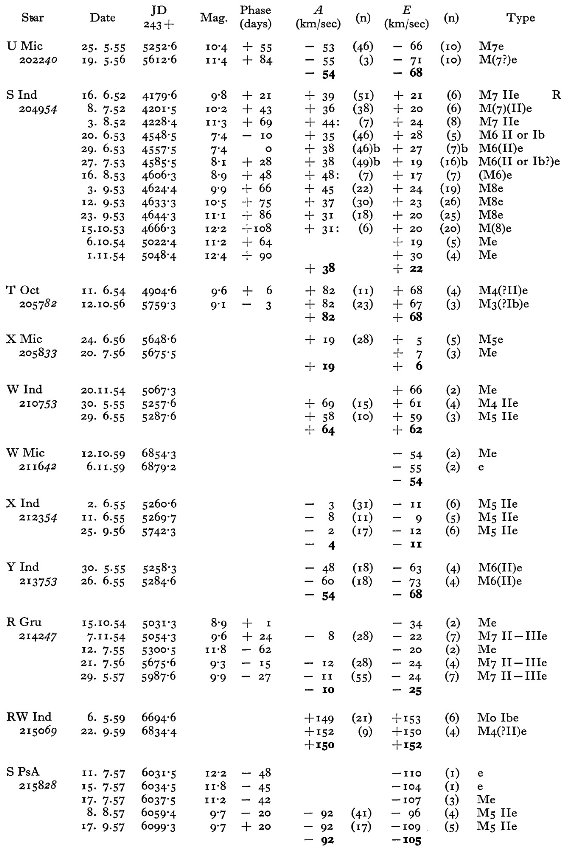
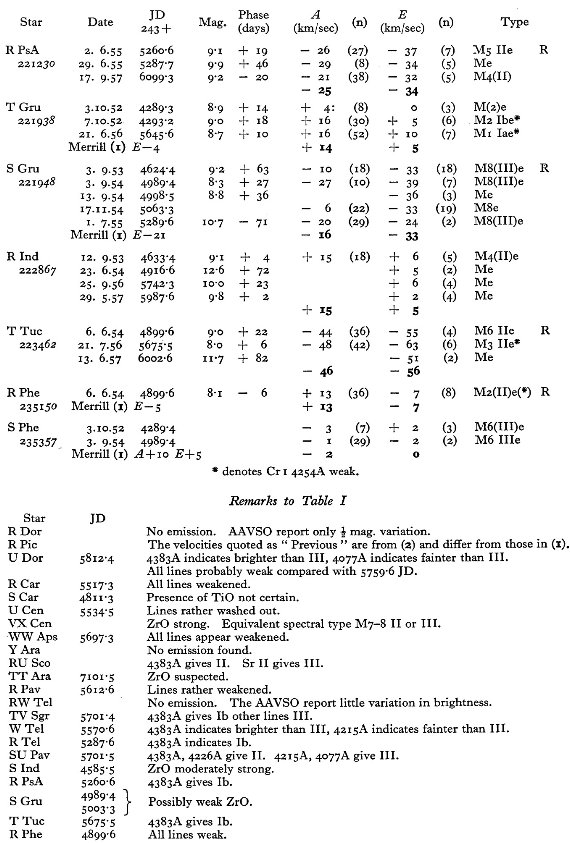
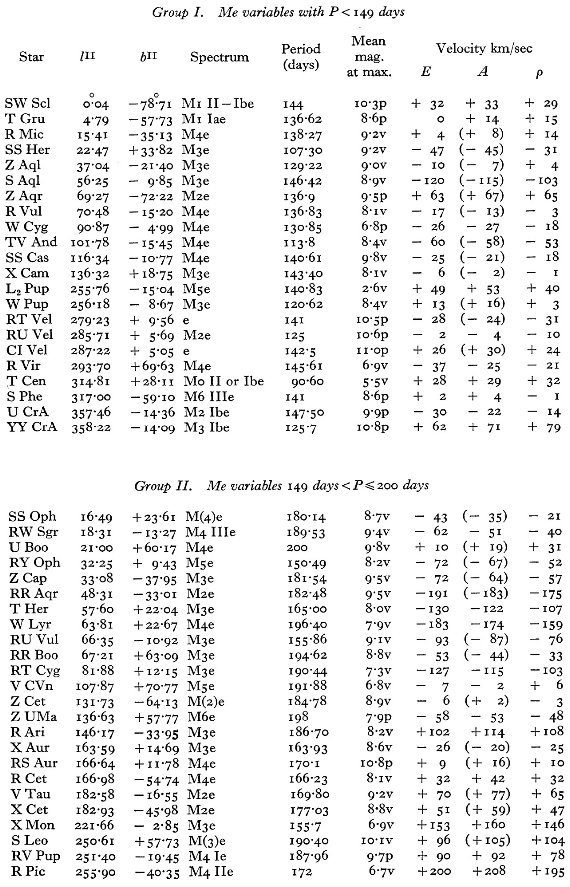
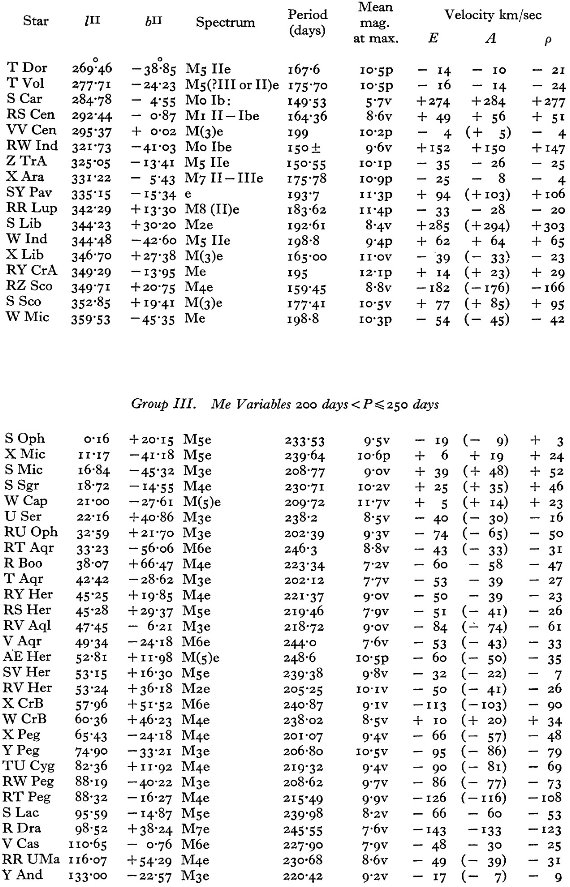
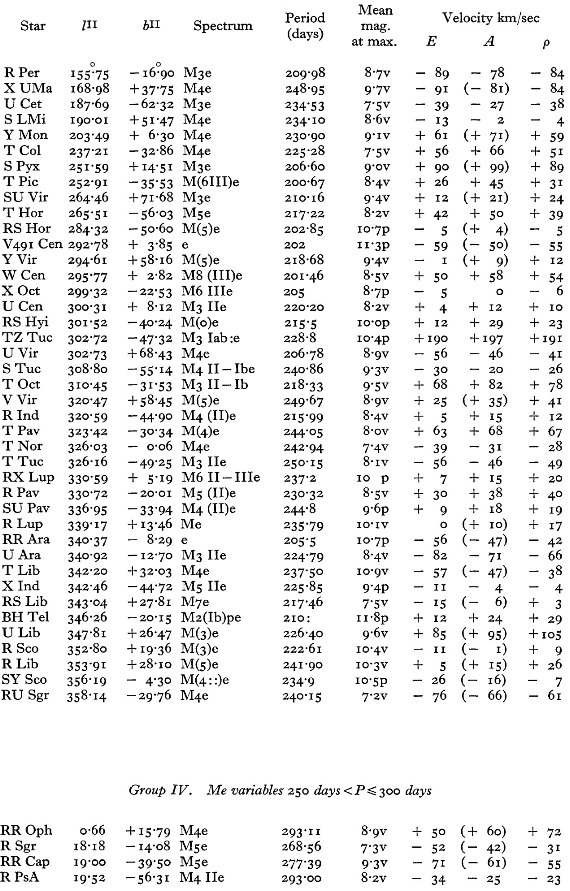
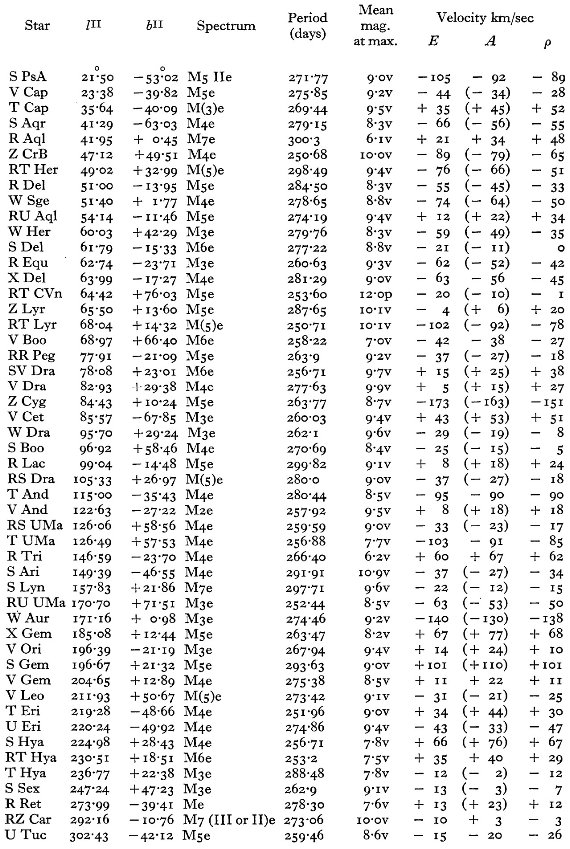
表1には主に南天の 114 長周期変光星に対する 281 分光観測からの視線
速度を記す。輝線と吸収線のそれぞれに、波長と速度を示す。異なる輝線間の
速度差を議論し、図1では輝線速度 - 吸収速度の周期との関係を示す。この
関係を用いて、輝線速度しか測れなかった星の吸収速度を決定した。表2には
405 長周期変光星の速度を周期に基づいて9つの集団に分けて示した。 第6章では S Ind 1953 年サイクルの詳しい解析から極大直後に速度が急速 に変化することを示した。第7、8章では Me 変光星のスペクトル型と光度ク ラスを与えた。光度におおきな広がりが、特に短周期で、あることが示唆され る。平均結果は統計的視差と合う。CrI 4254/FeI 4250 比の異常は以前 47 Tuc で見出された結果と合う。 353 Me 変光星は周期で 7 集団に分けられ、太陽運動を差し引いた残差速度を 解析した。K項は存在しない。銀河回転方向からのずれもない。第2章と図12 には、Me 変光星がほぼ全ての星種族タイプにまたがっている事が示される。 周期 149 日以下の星の運動の異常はこれらの星が第1倍音で振動していることを 示唆している。振動定数の比 Q0/Q1 = 2.4 は RR Lyr の 値より大きく、大きな Q0 = 0.056 と一致する。 Woolley-Eggen ク ラスのほしとの比較から、長周期の変光星がヒアデス巨星と同じ年齢と質量を持つ ことが示された。 |
短周期の星は高メタル球状星団の 周期 0.45 日の RR Lyr と
同じ年齢と質量を持つ。Me 変光星の大部分は円盤種族と中間種族 II に属する。 15章では速度楕円を導いた。表5には様々な定数の平均値を示す。h/k (0.87 ±0.11) は極端種族I天体より大きい。銀河面から離れた所で、密度 勾配 ∂ν/∂R が通常星と異なる証拠はない。しかし、もし変光星 の見かけ分布から見出された高い勾配が確認されたら、それは θ c > 270 km/s という大きな回転速度を意味する。密度勾配は R が大きくなるにつれ緩くなる。h/l (0.77±0.14) は若い星の値より 大きく、Me 変光星が定常状態に近いことを示す。銀河面距離の平均は短周期 で 1500 pc, 長周期で 100 pc である。オールト定数の重み付き平均 A = 7.8 ±3.4 km/s/kpc が導かれた。これは極端種族Iに対するものよりずっと小さいが、平均周期 250 日の Me 変光星の速度楕円体からの予想と一致する。 Se 変光星の微分銀河回転からその Mv = -3.4 が導かれた。これは Takayanagi の値と一致する。しかし、最近の統計視差からの値より明るい。 |
|
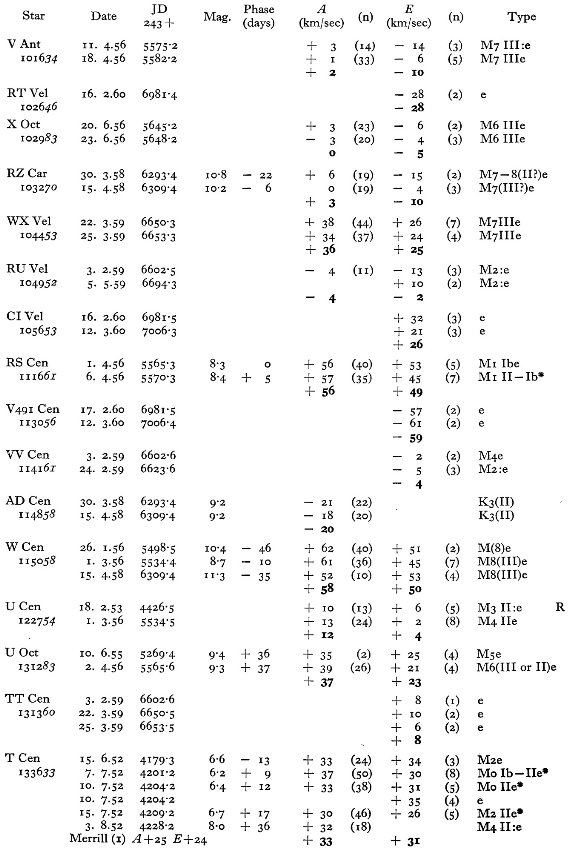
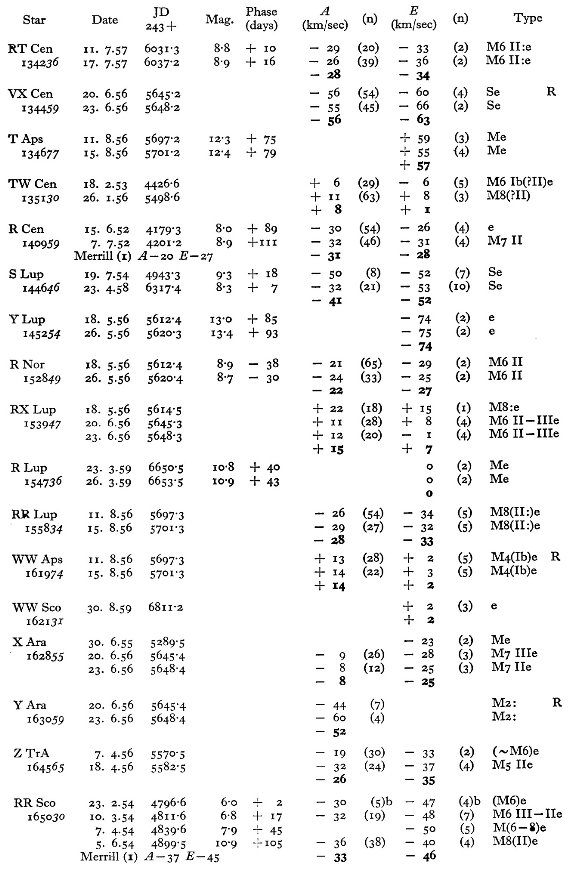
表1には主に南天の 114 長周期変光星に対する 281 分光観測からの視線
速度を記す。輝線と吸収線のそれぞれに、波長と速度を示す。異なる輝線間の
速度差を議論し、図1では輝線速度 - 吸収速度の周期との関係を示す。この
関係を用いて、輝線速度しか測れなかった星の吸収速度を決定した。表2には
405 長周期変光星の速度を周期に基づいて9つの集団に分けて示した。 第6章では S Ind 1953 年サイクルの詳しい解析から極大直後に速度が急速 に変化することを示した。第7、8章では Me 変光星のスペクトル型と光度ク ラスを与えた。光度におおきな広がりが、特に短周期で、あることが示唆され る。平均結果は統計的視差と合う。CrI 4254/FeI 4250 比の異常は以前 47 Tuc で見出された結果と合う。 353 Me 変光星は周期で 7 集団に分けられ、太陽運動を差し引いた残差速度を 解析した。K項は存在しない。銀河回転方向からのずれもない。第2章と図12 には、Me 変光星がほぼ全ての星種族タイプにまたがっている事が示される。 周期 149 日以下の星の運動の異常はこれらの星が第1倍音で振動していることを 示唆している。振動定数の比 Q0/Q1 = 2.4 は RR Lyr の 値より大きく、大きな Q0 = 0.056 と一致する。 Woolley-Eggen ク ラスのほしとの比較から、長周期の変光星がヒアデス巨星と同じ年齢と質量を持つ ことが示された。 |
短周期の星は高メタル球状星団の 周期 0.45 日の RR Lyr と
同じ年齢と質量を持つ。Me 変光星の大部分は円盤種族と中間種族 II に属する。 15章では速度楕円を導いた。表5には様々な定数の平均値を示す。h/k (0.87 ±0.11) は極端種族I天体より大きい。銀河面から離れた所で、密度 勾配 ∂ν/∂R が通常星と異なる証拠はない。しかし、もし変光星 の見かけ分布から見出された高い勾配が確認されたら、それは θ c > 270 km/s という大きな回転速度を意味する。密度勾配は R が大きくなるにつれ緩くなる。h/l (0.77±0.14) は若い星の値より 大きく、Me 変光星が定常状態に近いことを示す。銀河面距離の平均は短周期 で 1500 pc, 長周期で 100 pc である。オールト定数の重み付き平均 A = 7.8 ±3.4 km/s/kpc が導かれた。これは極端種族Iに対するものよりずっと小さいが、平均周期 250 日の Me 変光星の速度楕円体からの予想と一致する。 Se 変光星の微分銀河回転からその Mv = -3.4 が導かれた。これは Takayanagi の値と一致する。しかし、最近の統計視差からの値より明るい。 |
 |
 |
 |
 |
 |
 |
 |
 |
Merrill 1940 は長周期変光星では極大付近の吸収線視線速度が星本体の
視線速度に近いことを示した。また、Ludendorff, Merrill は輝線視線速度
E は吸収線視線速度 E より系統的に低いことを示した。図1aには (A-E)
と 周期 P との関係を示す。一般的に (A-E) は P と共に増加する。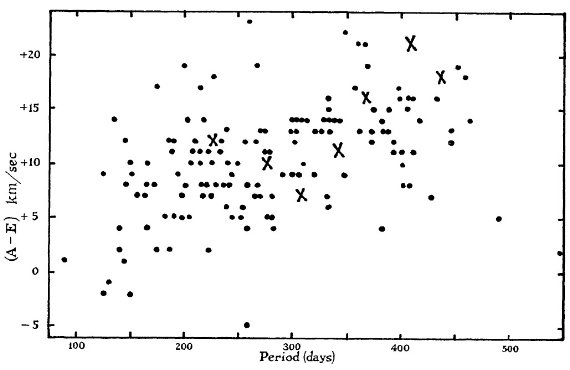 図1a.長周期変光星の (A-E) と P との関係。黒丸= Me 変光星。 バツ= Se 変光星。 |
図1b には図1a の平均を結んだ曲線を示す。Merrill の以前の曲線にあっ
た P = 210 d の極大と P = 270 d の極小がサンプル星の増加と共に小さく
なってきている。吸収線速度が得られたのは 86/114 星で、輝線のみの星は図1b
を用いて吸収線速度に変換する。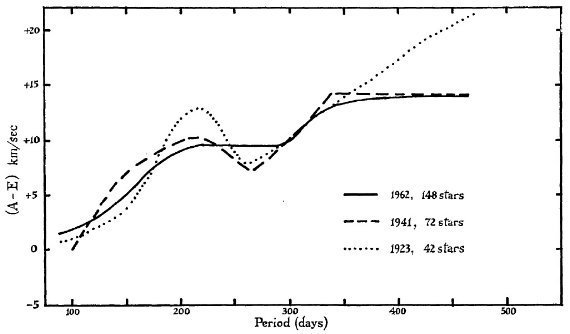 図1b.長周期変光星の (A-E) と P との関係。実線=図1a の平均曲線。他の 線= Merrill が以前に与えた曲線。 |
 図2.(a) S Ind 1953 年の光度曲線。(b), (c) S Ind 1953 年の視線 速度。 (d) U Ori 輝線速度 (1927 年) |
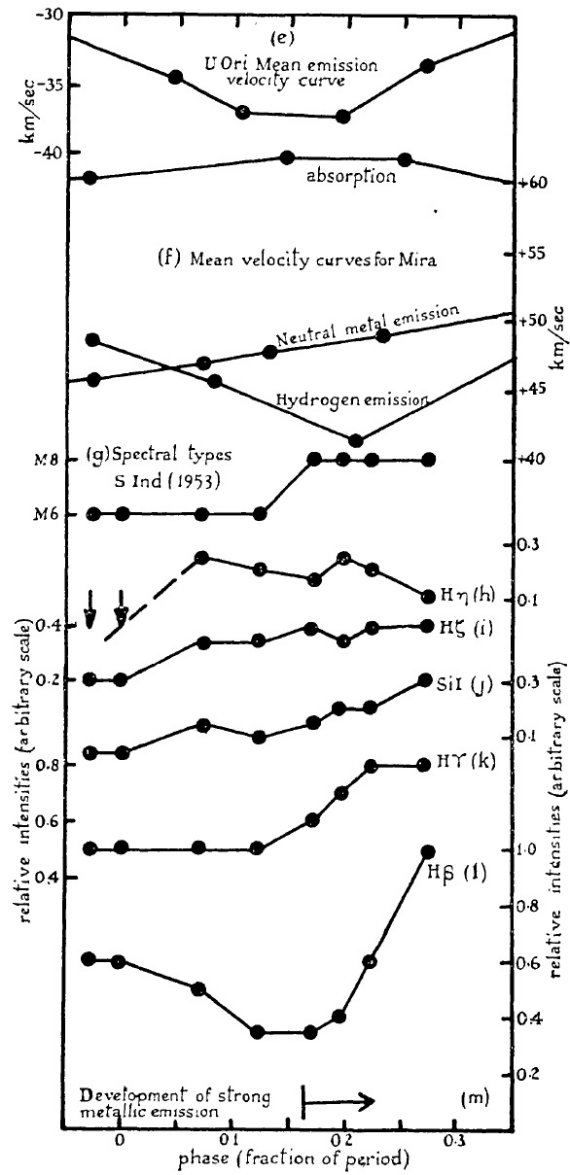 図2.(e) U Ori 過去数サイクルの平均輝線速度。(f) ミラの過去数サイクルの平均速度。 (g) S Ind のスペクトル型。(h) - (m) Hγ を基準にした線強度。 |
|
スペクトル型 Keenan から提供された標準スペクトルを使って、スペクトル型を決めた。 それらは表1に示される。一般にスペクトル型は周期と共に晩期になる。 光度 Keenan 1942 に従って変光星の光度クラスを定めた。図3には光度クラスと 周期の関係を示す。図の右軸には Keenan (in Stellar Atmosphere 1960) から 採った実視絶対等級を記す。Me 変光星の光度は通常、視線速度と固有運動の 統計視差から求められる。最近の研究については Osvalds, Risley 1961, そのまとめは Osvalds, Risley (1961) にある。 しかし、特に P < 250 d の短周期ミラでは、 その分散はかなり大きいと疑われる。 RT Cyg と X Mon RT Cyg と X Mon の光度は個々に求められた。将来の検討が必要。 周期光度関係 一般には Wilson, Merrill (1942) の周期光度関係が広く使われている。より最近の結果としては、 Osvalds, Risley (1961) がある。散らばりが大きいので、平均曲線の有用性は疑われるが、 両者が大体同じ傾向を与えていることは喜ばしい。特に、長周期変光星 では、 Osvalds, Risley (1961) の結果は分光から得られた光度と良い一致を示している。 スペクトル 型が M4 より早期で光度クラスが II かそれより明るい星は全て周期が 250 d より 短い。輻射等級は勿論周期と共に増加する。 ( ”増加”の意味が?) |
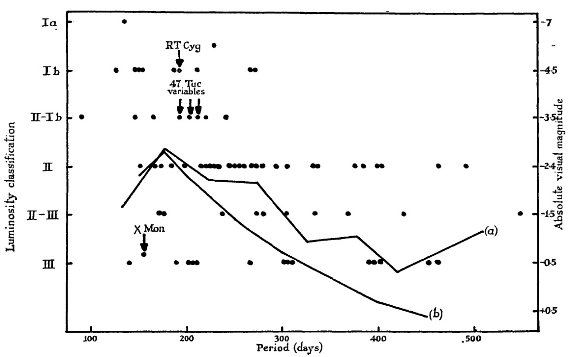 図3.Me 変光星の光度クラスと周期との関係。47 Tuc 内の3つの長周期変光 星と本文で引用された RT Cyg、 X Mon をマークした。曲線=統計視差から 導いた光度クラス。(a) = Osvalds, Risley (1961) (b) = Wilson, Merrill (1942) |
 |
 |
 |
 |
 |
 |
 |
 |
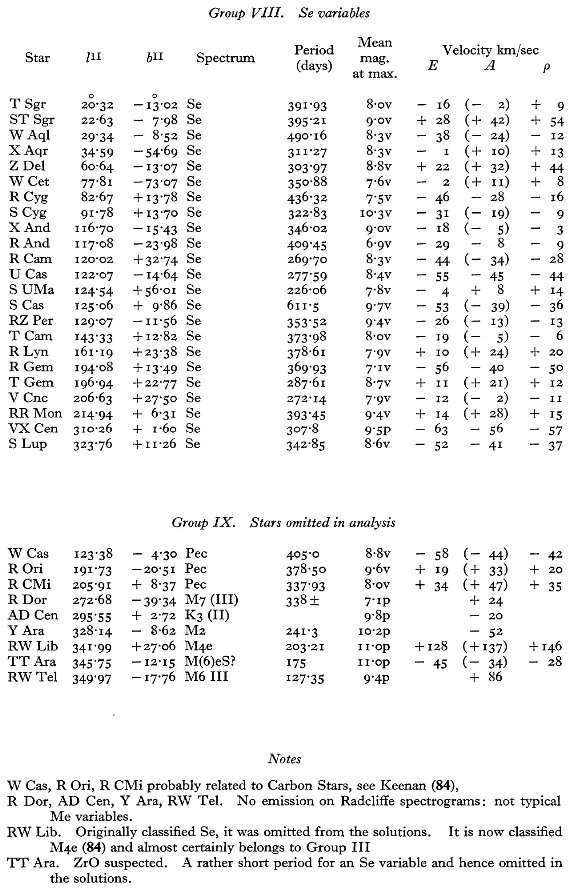 |
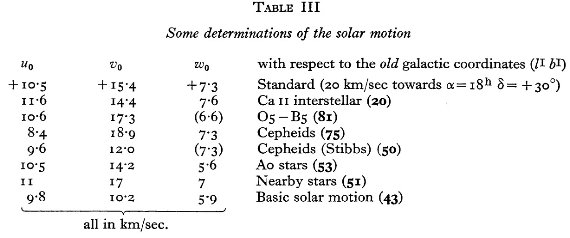 表3.様々な方法により決定された太陽運動 |
|
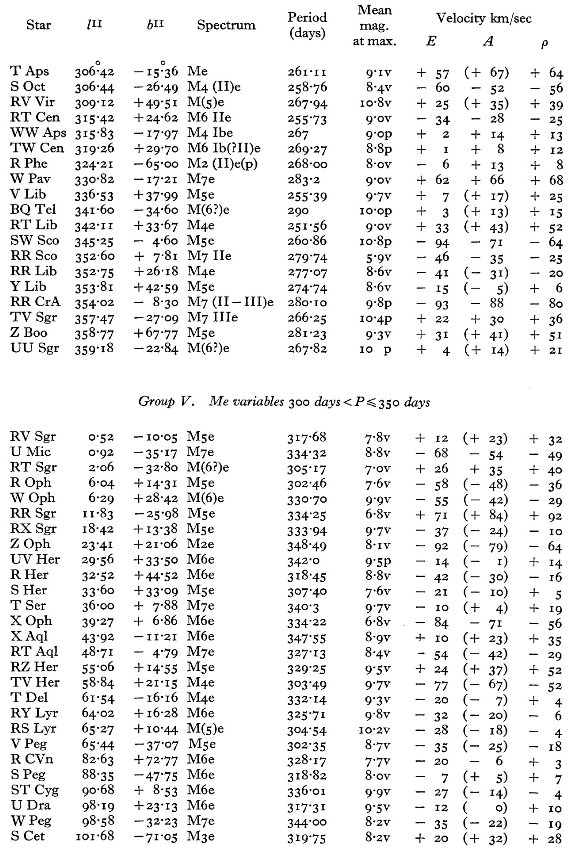
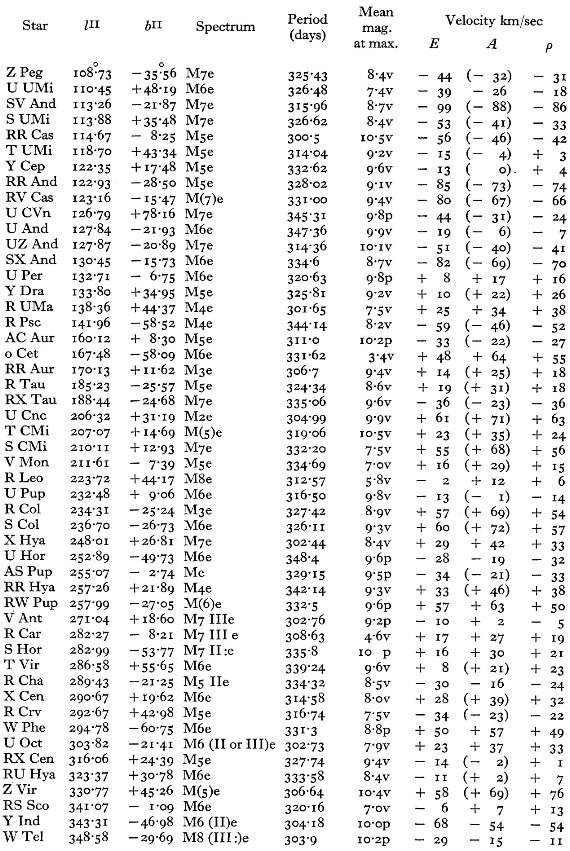
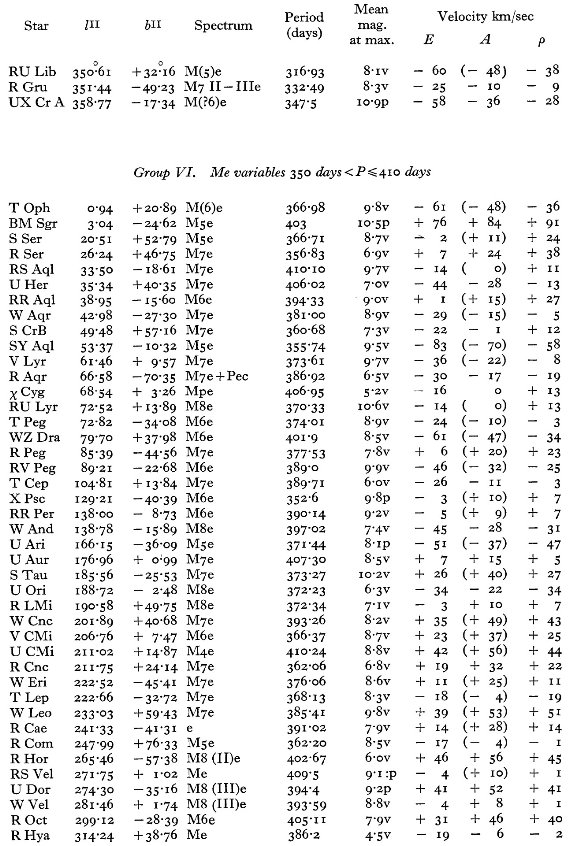
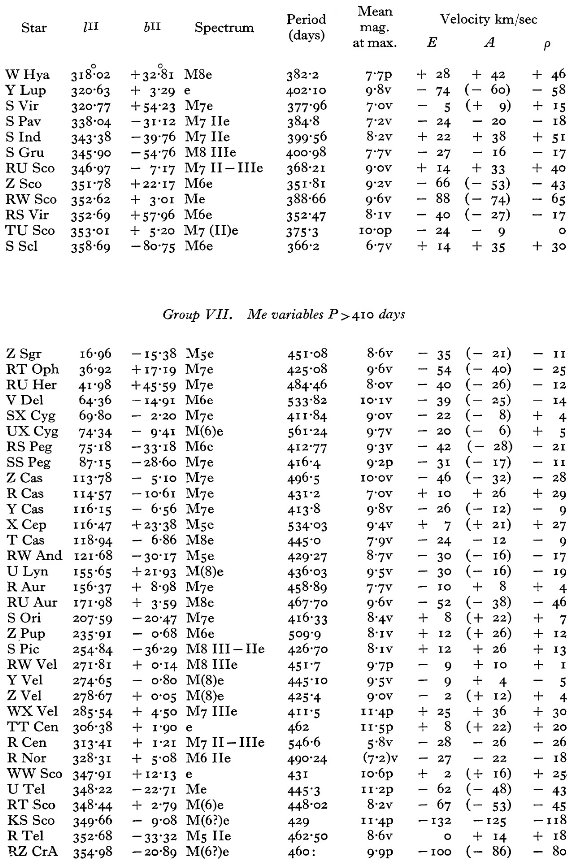
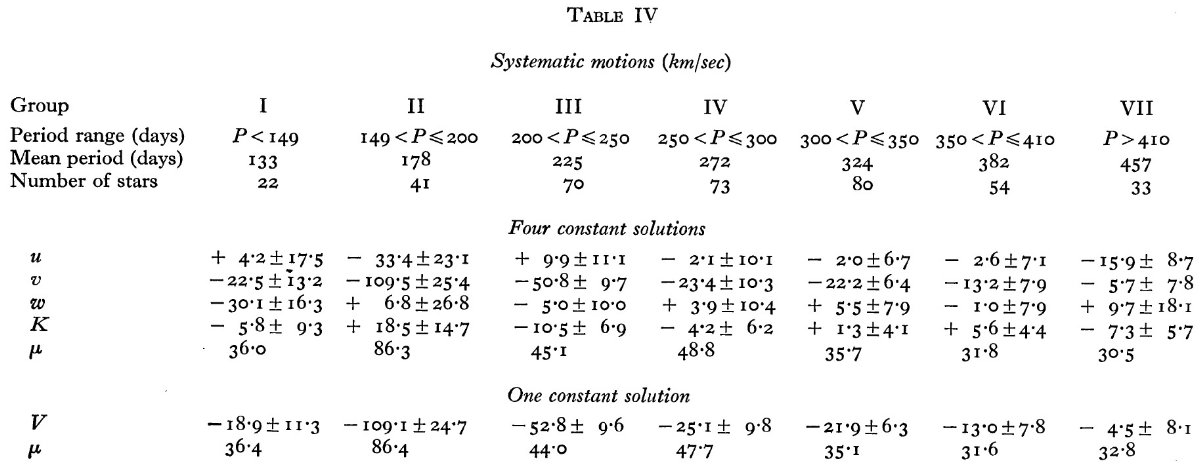
サンプル星が増え、一様度が増した 表2には 373 の Me 変光星が載っている。Dec < -30 の星が増えたこと で、総数は 25 % の増加となった。天空上の分布がより一様になったので統計 解析の信頼度が増した。 P = 150 - 200 d に残差速度ピーク 図4には残差速度と周期の関係をプロットした。 P = 150 - 200 d で高速度 になり、両側で落ちる特徴がはっきりと見える。速度分布をさらに調べるため に全体を周期区間で7つに分けた。この分割はスペクトル型による区分よりも 基本的である。周期による分割のパラメタ―は表4に示した。 |
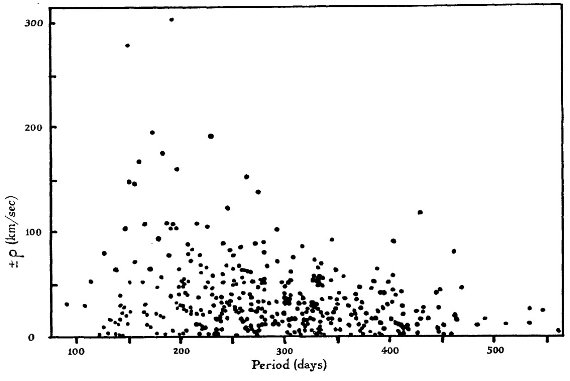 図4.Me 変光星の残差速度 (ρ) と周期の関係 |
|
系統運動の式 系統運動は次の式を解いて求める。 u cos l cos b + v sin l cos b + w sin b + K = ρ 結果は表4にある。 K, u, w はゼロから大きくずれていない。また、それらの 周期依存も見られない。ただ、グループ1の w のみはエラーの倍ゼロからずれ ているがサンプル数が小さいので有意かどうか不明。 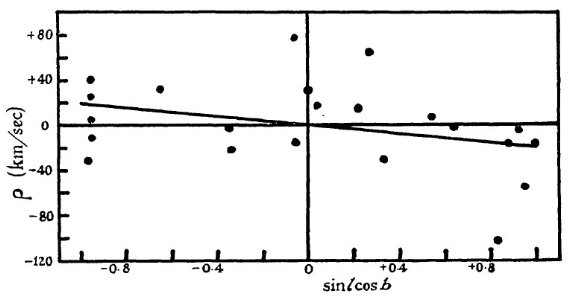 図5.グループ1 (P < 149 d) の残差速度 ρ と sin l cos b の関係。 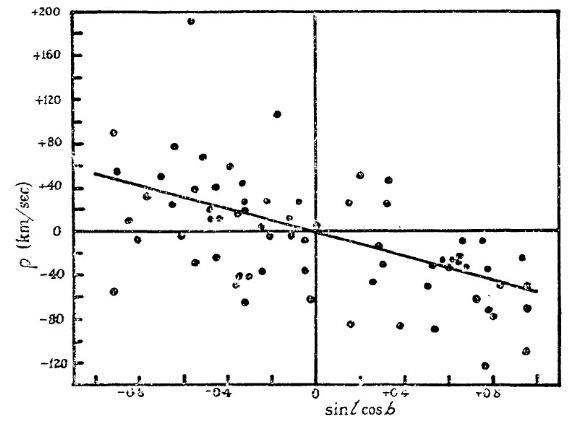 図7.グループ3 (200 d < P ≤ 250 d) の残差速度 ρ と sin l cos b の関係。 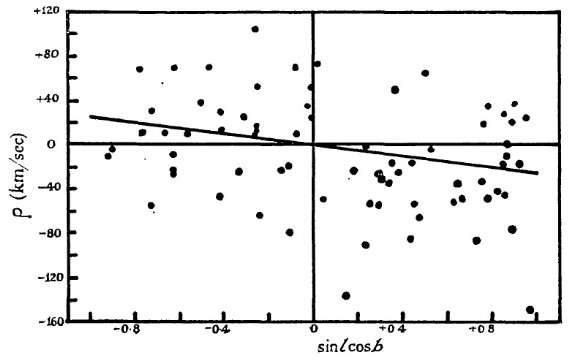 図8.グループ4 (250 d < P ≤ 300 d) の残差速度 ρ と sin l cos b の関係。 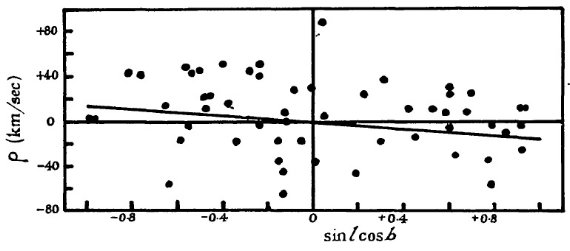 図10.グループ4 (350 d < P ≤ 410 d) の残差速度 ρ と sin l cos b の関係。 |
K = 0 K = 0 は重要である。これは視線速度 A が星の真の視線速度を現していて、 大気運動で系統的な影響を受けていないことを示すからである。K, u, w = 0 として、 V sin l cos b = ρ を解いた結果も表4に載せた。この解は 図 5 - 11 に引いた。 速度種族はあるか? これまで、Me は一様なグループとして扱ってきた。ある周期に対する光度の 分散は大きい。しかし、Me が二つの、例えば種族 I と II グループ、それぞ れが一様なグループに分かれるという証拠はない。ただ、図6を見ると、グル ープ2の星は二つに分かれるかも知れない。一つは V = 250 km/s, もう一つは V ≤ 50 km/s である。 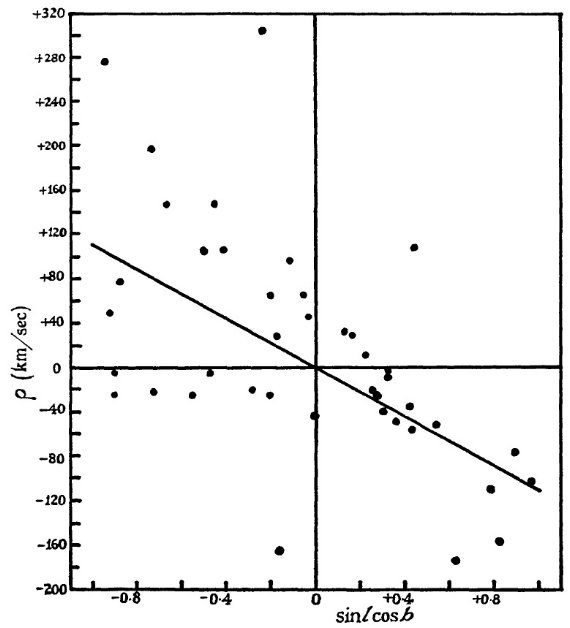 図6.グループ2 (149 d < P ≤ 200 d) の残差速度 ρ と sin l cos b の関係。 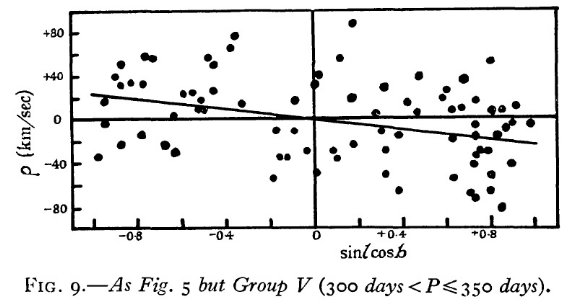 図9.グループ5 (300 d < P ≤ 350 d) の残差速度 ρ と sin l cos b の関係。 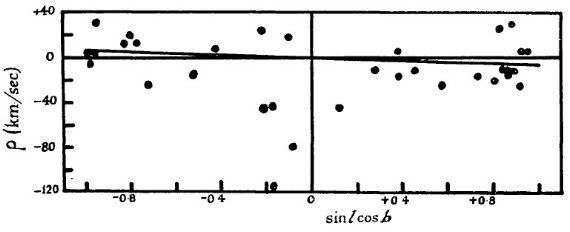 図11.グループ7 (410 d < P) の残差速度 ρ と sin l cos b の関係。 |
|
Woolley, Eggen 1958 クラス 図12には V と Me 変光星の周期との関係を示す。 Woolley, Eggen (1958) は太陽近傍の星の軌道をその離心率から A - E+ の6クラスに分けた。彼らはその 6クラスがヒアデスの属するクラスAから M67 のクラスE+まで平均年齢に 対応することを示した。Me の周期グループの平均 V は Woolley, Eggen クラス の夫々に対応する。 グループ 7 = Ao 型星クラス Me 変光星の周期が下がると V が上がること、ただ、 P < 149 d の Me 変光星だけは V が小さいことは以前にも Keenan 1959 が注意していた。 今回の結果はそれを明瞭に示した。当座、P < 149 d グループを脇に置いと いて、P = 450 d 付近のの星は Woolley-Eggen クラス A かそれより若いくらいの 星に対応する。これは古い種族 I で Ao 型星と同じ運動特性が期待される。 Alexander 1958 による Ao 星の u, v, w 決定値は表3に載せた。 太陽運動を引くと、その V = -4.0 km/s は確かに Me グループ 7 に一致する。 グループ2=極端種族 II グループ2 P = 175 d の V は種族 II 成分、ただし球状星団や準矮星ほど 古くはなく、 P = 0.45 d 程の RR Lyr 星に対応する。バチカン会議では P > 0.4 d の RR Lyr は極端種族 II に分類された。 中間グループ=中間種族 II と 円盤種族 グループ3−6の Me 変光星は中間種族 II と 円盤種族に属する。 |
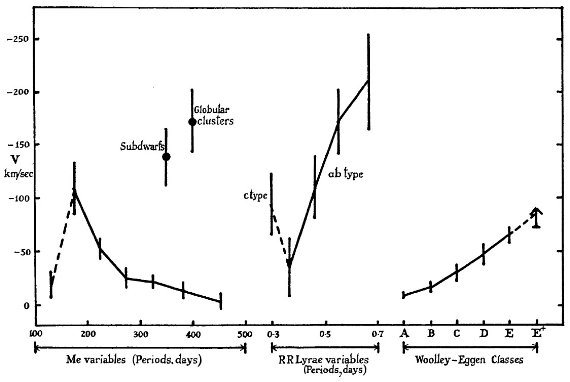 図12.様々な星の系統速度 V .(1) Me 変光星の周期グループ。(2)RR Lyr の 周期グループ。(3) 準矮星。(4) 球状星団。(5) Woolley-Eggen クラス A - E の 星。 |
4.4.P < 149 d の Me 変光星一般関係からの外れP < 149 d の Me 変光星は V と P の一般的な関係には従わない。その 平均 V は周期 330 日程度の変光星と同じである。固有運動から導いたこの グループの平均絶対等級も図3にある一般的な周期等級関係から外れている。 その帯は周期 300 日グループのそれに近い。 RR Lyr 星の場合 RR Lyr 星では、c タイプが周期・運動関係の一般傾向と合わない。球状星団 での観測から、これらは第1倍音で振動しているのではないかと言われる、 同様の状況が古典セファイドでも見られ、 Eggen の AB タイプと C タイプを 生んだ。RR Lyr c タイプの運動が ab タイプの長周期グループと近いことは、 倍音仮説と一致する。従って、グループ I Me 変光星に同様の説明が可能かも 知れない。 基準振動と倍音振動 グループ1は第1倍音で振動していると仮定する。すると、振動定数の比は 周期の比と等しいので、Q0/Q1 = P0 /P1 である。図12から Me 変光星の場合、Q0/ Q1 = 2.4 である。この値は実は基準振動と倍音振動で平均密度等が 同じでないと成立しない。しかし、補正法が分からないので第1近似として 2.4 を採用する。こうして、P = 300 d グループが基本振動であり、 グループ1 が第1倍音となる。 |
4.5. Me 変光星の年齢と質量両極端長周期 Me 変光星の運動は Woolley-Eggen クラスA と近い。このクラスは ヒアデスと似た CMD を持つ。そのターンオフ質量は 2.5 Mo, 年齢 500 Myr である。 一方、短周期(ただし P < 14 d 除く)変光星は RR Lyr と運動が重なり、 少なくとも一つの球状星団 47 Tuc に属している。球状星団の年齢は不確定だが 10 - 20 Gyr の範囲である。ターンオフ質量は 1 Mo 近い。 連星 X Oph と Mira は連星でありそれから出した質量は 1 Mo に近い。 中間グループ 中間グループは先の両極端の間にあるだろう。 |
4.6.振動定数早期 M-型星の Q
別の表現では、
晩期型巨星では TiO が強く、輻射補正の不定性が大きいため、下式の適用は 難しい。しかし、早期 M 型では可能である。もし、 P = 200 d, M = 1 Mo, スペクトル型 M0, Te = 3000 K, BC = -2.3 mag、Mv = -2.7 mag とすると、 Q = 0.068 が得られる。 ミラの Q より長周期のミラ P = 332 d に対しては, 図3から絶対等級 -1.2 mag を とり、対応する視差 -0".012 から R = 480 Ro を得る。 M = 2 Mo とすると、 Q = 0.044 である。 Me 変光星の Q そこで両者の平均を取り、 Q = 0.056 を Me 変光星全般に適用する。 |
4.7.速度楕円体表4に速度楕円体パラメターMerrill の視線速度解析は Oort, van Tulder 1942 が解析した。今回はより 数が多く、方向カバーが完全なデータを用いて、7グループの夫々に対して 速度楕円体パラメターを求め、表4に示した。 パラメターの決定 サンプル数の少なさから、速度楕円体の軸方向のずれは考えない。 すると、グループ速度からの残差の分布は下のようになる。 exp(-h2u2 - k2v2 -l2w2) ξ = peculiar velocity = グループ速度からの残差、とすると、 α2(cos i cos b)2 + β2 (sin l cos b)2 + γ2(sin b)2 = ξ2 ( ξ2 は 全方向の 残差視線速度の分散のことか?) ここに、h = 1/(α21/2), k = 1/(β21/2), l = 1/(γ21/2) である。7つのグループ毎に最小二乗法で α, β, γ を解いた結果を表5に示す。 グループ2の速度分散 α, β, γ の最大値はグループ2で起きる。グループ2は V の大きさも最大である。これは Stomberg 19?? の結果と定性的に合致する。 |
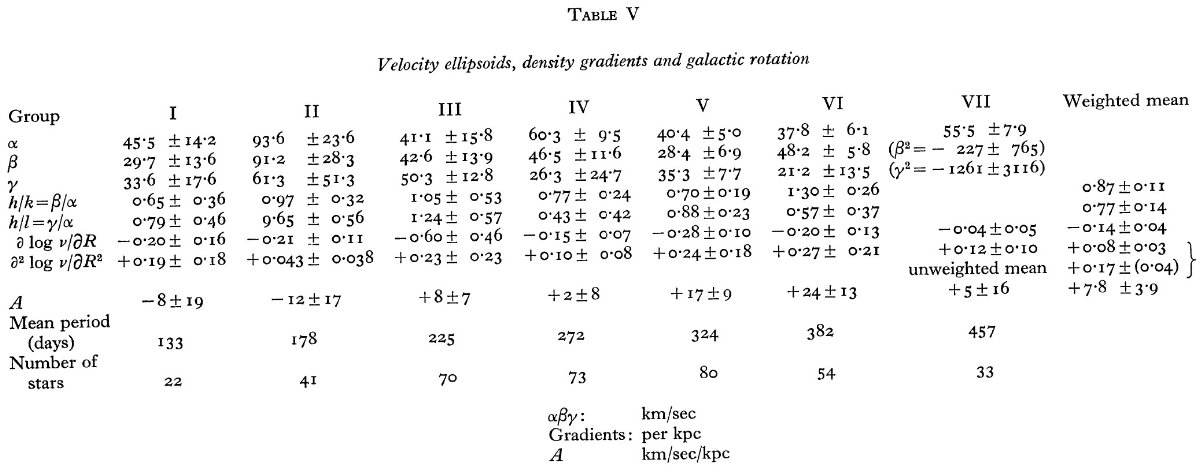
|
Me 変光星の h/k 表5を見ると、h/k が周期に依らない一定値である。表6には h/k を幾つかの種類の星に対して示す。極端種族 I の値はオールト定数 A, B から求めた。表5から Me 変光星の h/k は他の種類の星と異なることが 分かる。 h/k と密度勾配 Oort 1928, 1942 によると、定常状態では h/k は密度勾配に依存する。ν = 密度、R = 銀河中心からの距離、θc = 太陽位置での銀河 系回転速度、θ0 = θc - V とすると、
上で得た β/α を使い、銀河回転に 220 km/s, R = 8.9 kpc を代入 すると、表5に載せた ∂log ν/∂R を得る。この値に周期による 系統的変化がある積極的な証拠はない。そこで、表5に重み付き平均を載せた。 表7には様々な勾配値を比較した。 Oort の値との比較 略 |
 表6.h/k の値  表7.平均密度勾配の比較 |
|
力学緩和すると h/l = 1 定常状態理論によると、動径方向散布度 α は銀極方向散布度 γ と等しい、つまり h = l となる。様々な恒星グループを調べると、表5のよう に α > γ (h < l) である。これは力学的緩和に達する時間 が非常に長いためと考えられる。 |
銀河面距離 周期が小さくなると z 方向の速度散布度は大きくなる。銀河面に垂直な方向 の重力を使うと、長周期変光星は銀河面平均距離が 100 pc であるのに対し、 短周期では 1.5 kpc となる。これは以前に導いた結論、Me 変光星は実際上 恒星種族の全年齢巾をカバーしている、を支持する。Oort 1958 によると、 銀河面平均距離は極端種族 I で 120 pc, 種族 II で 2 kpc である。 |
|
小さな A グループ速度からの残差速度 ξ を使って微分回転が調べられる。 周期と絶対等級に関する Osvald, Risely 1961 の関係を使い、適当な減光則 で距離を決める。オールト定数 A は次の式から最小二乗で決まる。 ξ = A r sin 2l cos2l 各グループの A は表5に載せた。平均値は A = 7.8 km/s/kpc である。 極端種族 I の星を除き、微分回転の証拠が見つかったのは Me 変光星のみである。 エラーは大きいが、A のこの値は最近 B-型星とセファイドに対して決まった A = 17.5 に較べると大分小さい。 オールトの A Oort, van Tulder 1942 も Me 変光星に対して小さな A を得た。彼らが使っ た式は
|
ここに、θc = 220 km/s, R = 8.9 kpc, h.k = 0.87
を代入すると A = 5.0 km/s/kpc が得られる。 表5から各グループに対する A を求めると、A が V に依存しているように も見える。ただし精度が低いのではっきりしない。 オールト定数 B オールト定数 B は A - B = (θc -V)/R で表される。上の A を用いると B = -15 km/s/kpc が得られる。将来この値の チェックが固有運動から行われるだろう。 |
|
再解析の必要性 表2には 23 個の Se 長周期変光星がグループ8として登録されている。データ は主に Merrill である。最近 高柳 1960 は Se 変光星の解析を行った。しかし、 ここでは図1の新しい A-E 関係により、多くの星の速度が変化したので、再解析 を行う。それにこの論文で加えた二つの Se 変光星は第3象限にあるので、これまで 掛けていた方向が埋まるという重大な変化が加わる。 Se 変光星の絶対等級 Osvalds, Risley 1961 は Se 変光星の平均可視絶対等級として -1.56 mag を与えた。この値から導いた A = +34 km/s/kpc は大きすぎる。この種族に 対しては A = 15 が期待される。Se の光度を低く見積もり過ぎている。Mv = -3.4 が適当である。 |
高柳 Mv = -3.4 は高柳 1960 の結果とも一致する。かれはまた、固有運動から Mv = -3.0 を導いている。 周期光度関係 Me 変光星の質量が周期と共に上がることは前に述べた。 Se 変光星は 3 Mo より重いグループに属するように見える。そうだとすると、同じ周期で較べると Se 星が Me 星より明るくなるので、周期光度関係に不連続が生じる。 Ce 変光星 Ce 変光星はここでは議論しない。色々な証拠から Ce 星は Se 星と共に極端 種族 I に属すると考えられる。与えられた質量の星が Se, Ce を経て進化する のか、両者は別の質量なのか今の所不明である。 |
|
|
|
