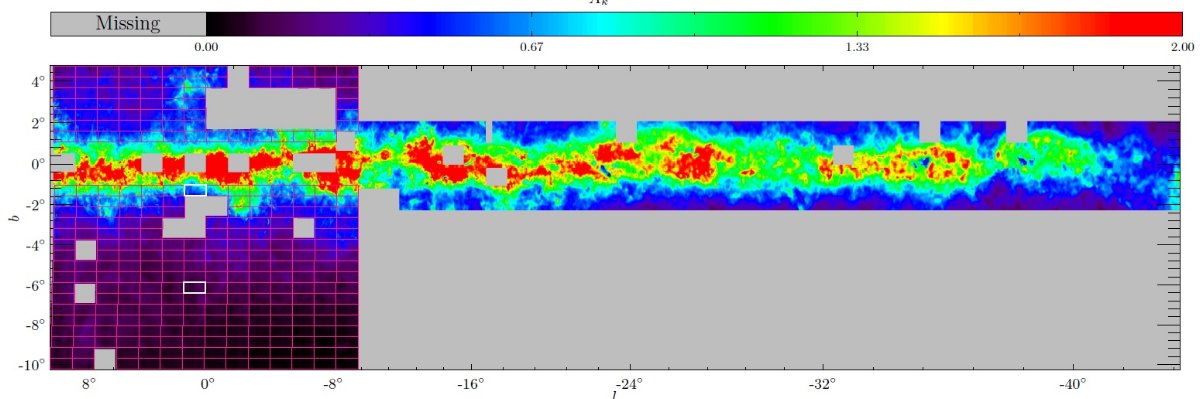
| 内側銀河系では円盤不安定性から生じたと考えられるボクシー3軸不等バルジ が支配的である。その近さに拘わらず、我々が不透明な円盤中にあるため、その 大規模構造は未だに良く知られていない。 VVV サーベイの DR1 を用い、レッドクランプ星を用いたバルジの3次元分布 を示す。視線方向の密度分布は Ks 分布に減光と検出度の補正を行って求めた。 モデル化に当たってはバルジは8重の対称性を保持すると仮定した。 | そうして、バー主軸の傾きを (27±2)° と求めた。得られた密度 分布は非常に細長く、軸比が 10;6.3;2.6 で指数関数型スケール長= 0.70: 0.44-0.18 kpc である。銀河面から 400 pc 上でバルジの密度分布はX字構造 を示す。全体としての構造は棒銀河に特有なボクシーでピーナツ型の形を している。 |
|
X字構造 Stanek et al 1997 と Rattenbury et al 2007 は Dewek et al 1995 の 3次元モデルに OGLE-II データをフィットした。McWilliam, Zoccali 2010 は 2MASS データから高銀緯帯ではバルジが二つに分かれ、それは棒銀河に 特有な X-字型構造によるものとした。Saito et al 2010 は 2MASS RC 星 からバルジ全体構造を調べ、X字構造を確認した。 |
VVV は深い この論文では VVV DR1 データ(Saito et al 2010) を用いて、先行研究を 拡大する。VVV は 2MASS より 4 mag 深いので、最も減光の強い領域を 除いては、全 RC 星を検出できる。 Lopez-Koredoira et al 2001, 2005 法 ここでの方法は、RC より明るい星の光度関数を用いてバルジ3次元構造を 調べた Lopez-Koredoira et al 2001, 2005 に倣う。ただし、 RC 星はその 目的にはより優れていて、|b| ≥ 1 を良く調べることが出来る。 |

|
Gonzalez et al. 2011 の減光補正法 まず、 Gonzalez et al. 2011 の方法で減光補正を行った。以下に概要を述べる。 (i) ゼロ点 VVV DR1 ゼロ点を 2MASS ゼロ点に変換する。VVV の基準ゼロ点は RC ピーク付近で 0.1 mag ていどのばらつきがある。そこで、明るい VVV 星 の等級を 2MASS と合わせることでフィールド毎にゼロ点を決め直した。 (ii) 減光補正 減光マップ AKs(l, b) から Kso = Ks - AKs(l, b) で減光補正等級を得る。減光は全て太陽とバルジの中間で起きると仮定する。 (iii) グリッドの平均 J-Ks カラー 1′×1′ グリッド内でレッド クランプの J-Ks カラーの変化を測り、色超過を決定する。グリッド内の レッドクランプ数が 200 以下の時は周囲から足して 200 にする。このため、 空間分解能は銀河中心の 3° 以内では 3′、b = -10 では 15′ と変化する。 (iv) E(J-Ks) E(J-Ks) = ⟨J-Ks⟩RC - ⟨J-Ks⟩RC,o. ここに、⟨J-Ks⟩RC,o = 0.674 は Gonzalez et al. 2011 がバーデの窓で決めた値である。 (v) 減光マップ Nishiyama et al. 2006 の減光則を用い、AKs = 0.528 E(J-Ks) として減光マップを 作製した。 比較 図1には減光マップ、図2には我々のマップを Gonzalez et al 2012 と比較した。一致は非常に良い。 メタル量勾配 Salaris, Girardi 200, Cabrera-Lavers et al. 2007 が示した通り、レッドクランプの MKs はメタル量に依存し、 バルジにはメタル量勾配(Zoccali et al 2008, Ness et al 2013)がある。 |
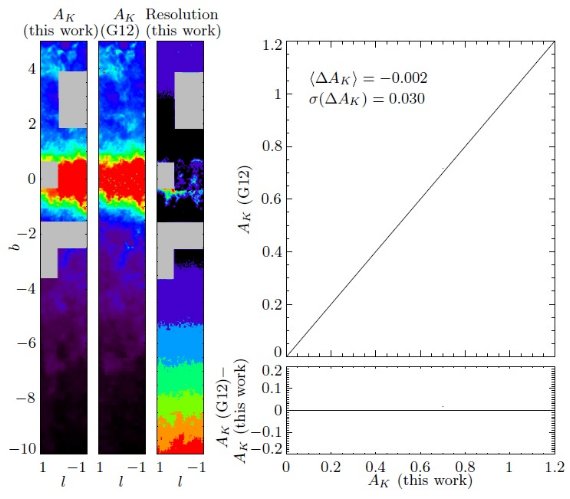 図2. Gonzalez et al. 2012 との減光比較。左:短軸に沿った減光の比較。右:|b| > 1° でランダム に選んだ 1000 点の比較。 低減光領域でのレッドクランプカラーの標準偏差は 0.05 である。 そこでのメタル量散らばりの標準偏差は Zoccali et al 2008 によると、 σ([Fe/H]) = 0.4 である。ここで考えている領域全体に亙っての メタル量変化は Δ[Fe/H] = 0.5 (Gonzalez et al. 2013) である。 そこでこれは、西山の減光則を使うと 0.528 x 0.05 x 0.5/0.4 = 0.03 となる。 (しかし、元々カラーの 散らばりはレッドクランプ固有のものではないのか? ) しかし、その効果はここでは無視できる。 |
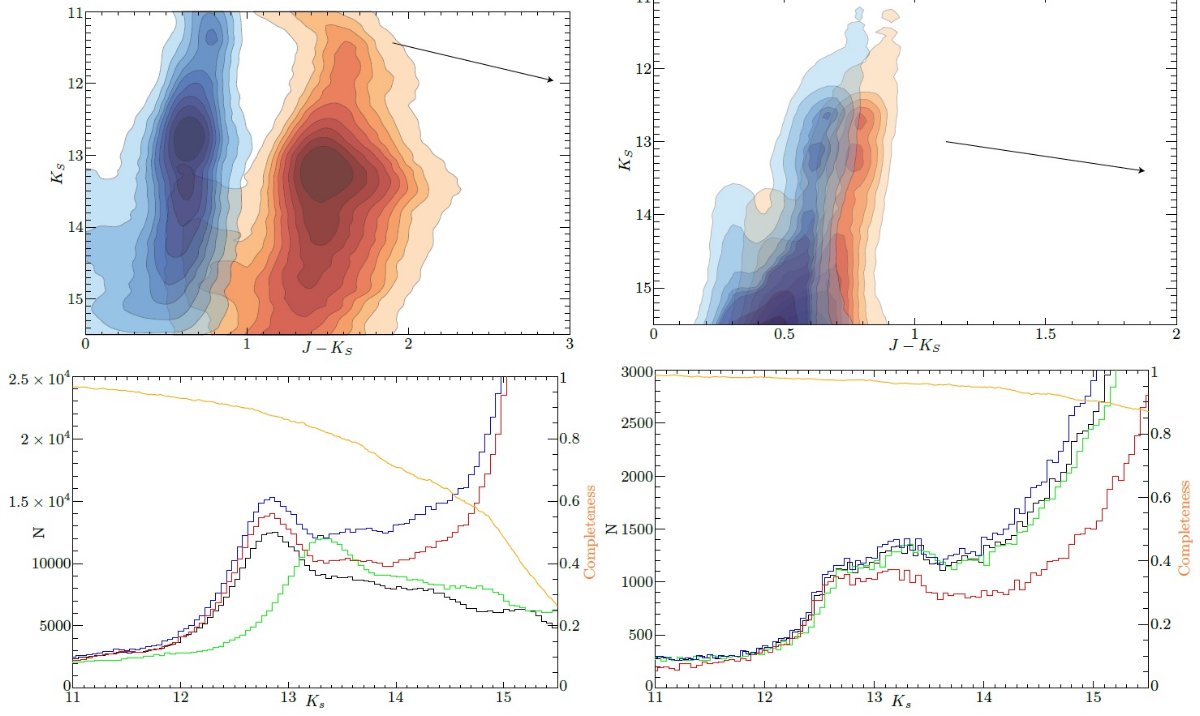
2.2.完全度人工星テストVVV でさえも円盤近くでは完全度が重要になる。人工星テストを行った。 20″&ims;20″ 枠毎にガウシャン PSF を 決定し、各 Ks 画像(大きさは?)毎に 20,000 個の 11 - 18 mag のテスト 星を入れて実験した。実験星の検出基準は入力値と位置で1ピクセル、等級 で 1 mag 以内とした。この実験を5回繰り返して統計エラーを下げた。 完全度曲線 こうして求めた完全度をカタログの各星に貼り付けた。これが図3に示した 完全度である。今後等級分布を議論する時には各等級ビンでの直接測定値 ではなく、完全度の逆数の和を使用する。 ( H の完全度、 Ks の完全度に対し、 H-Ks の完全度はどう定義する?カラーピークの決定などで。) |
2.3.カタログ個別カタログを合体各 VVV フィールドで作ったカタログを合体して最終カタログとした。 重なり合い部分ではフィールド中心が最も近い個別カタログの値を採用した。 球状星団(Harris 1996, 2010, Nataf et al 2013) の半光度半径の3倍以内 の星は解析から除いた。 レッドクランプのカラー分布 レッドクランプ中心カラーの 3σRC,JK 以内の星を レッドクランプ星として採用した。ここに σRC,JK は レッドクランプカラーの標準偏差である。検出 J のない Ks も保持しておくが、 それは完全度計算のためである。こうして得たカラー分布は図3の赤線として 示した。 明るい星は 2MASS Ks ≤ 12 mag では飽和と非線形応答の影響を受ける。従ってそこを 解析に使用する際は 2MASS を持ってきた。 その際の不連続を訂正するため、 11.9 - 12.1 mag で数を同じにした。 |
|
領域の再定義 VVV フィールドを Δl x Δb = 1.5 x 0.5 の区間に再定義した。 図1左のピンク色の区分けがそれである。|b| < 1 では減光と完全度補正 が大きすぎて信頼度が低いので解析から外す。 星計数の基礎方程式 N(Kso)dKs = 領域内の dKs にある星の数。Lopez et al 2000 より、 N(Kso) = ΔΩΣi∫Φi (Kso-5log[r/10pc])ρi(r)r2dr ここに、ΔΩ = 領域の立体角。和は異なる種族全体。 Φi(MKs) = i-種族の規格化光度関数。 ρi(r) = 視線方向の密度分布。 (機械的には ∂(MKs,r)/∂(Kso,r) = 1 だから。) (星計数は前節で選んだ RC 候補星についてか?選択があまりはっきり記述 されていなかったが。) 「背景」とレッドクランプ レッドクランプ以外の種族は滑らかに変化する「背景」を構成している と考える。それらは第1赤色巨星枝と円盤星からなると仮定し、レッドクランプ 星を別個に扱う。 N(Kso) = B(Kso) + ΔΩ∫ΦRC (Kso-5log[r/10pc])ρRC(r)r2dr この仮定に対する例外は、 RGBB = 赤色巨星コブ(Nataf et al 2011) でレッド クランプと同じくらいの等級散らばりを有す。そこで、赤色巨星コブを光度関数 の第2のピークとして含める。詳しくは3.1.節。AGB は RC の 3% 程度なので 無視する。 「背景」 背景光度関数は、log B で2次式であると仮定する。 log B(Kso) = a + b(Kso-13) + c(Kso-13)2 この表式を Ks = [11, 11.9], [14.3, 15] でフィットした。図4に フィットの例を示す。c は小さいが有意である。 (RC 候補をカラー基準で選んでおいて、星計数方程式では他の赤色巨星も 加えて解析するのは問題ないのか不明。それとも 観測等級分布はカラー選択なしで全部の星?) フィット区間の例外 「背景フィットに例外が二つある。それは l ≥ 5.5 と |b| ≤ 2 である。 |b| ≤ 2 では補正が大きすぎて、図3左に見られるように Ks = 15 付近で 背景が急上昇する。このような領域では c = 0 とし、フィットは Ks ≤ 14.5 に限定した。l ≥ 5.5 では、明るい方にレッドクランプ星が分布するので、 そこでは背景フィットの明るい側は Ks = [11, 11.7] に変更する。図6には b = 一定の背景の断面図を示す。 |
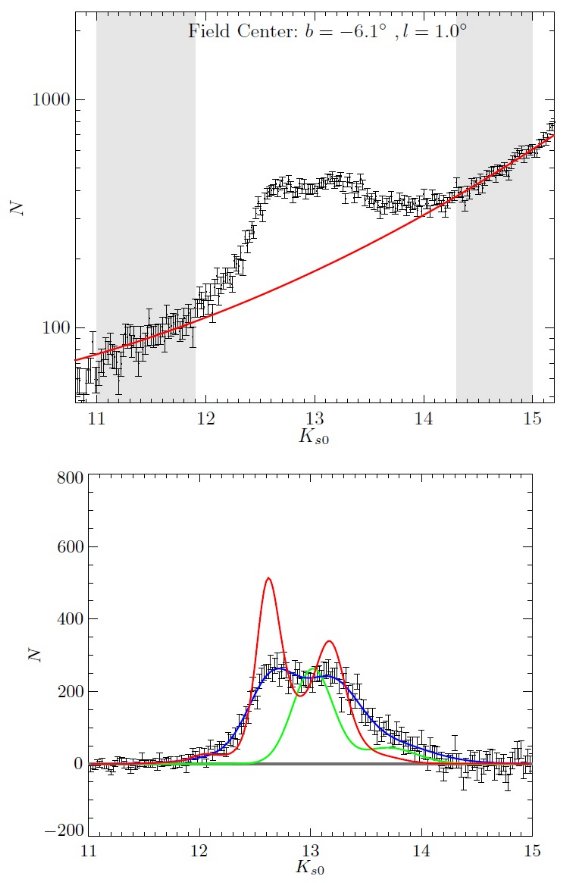 図4.デコンボリューションにより視線方向分布密度を再現する。領域は b250 で図3の右側に相当する。上:赤線=図両側の灰色部に2次式フィットした 背景。下:デコンボリューションを示す。赤=密度 Δ=ΔΩ (ln10/5)ρRCr3. 緑=仮定した光度関数。 青=再コンボリューションしたモデル Δ&astr;ΦRC. この図の場合、式10が満たされるので、62回の逐次近似が必要だった。 フィットの式は再コンボルブしたモデル(青)とデータの比較で決まる。 Δ の比較を容易にするため、プロットの際に中央において、レッドク ランプが有効的には MK, RC = 0 となるようにした。 |
|
モデル光度関数 光度関数=レッドクランプ+赤色巨星コブ+背景、と考える。I-バンドでは コブはレッドクランプより 0.74 mag 暗く、その数はレッドクランプの 20 % である。Nataf et al 2013 に従い双方の光度関数をガウシャンで近似する。 バルジの赤色巨星コブが Ks でどのくらいかは良く調べられていない。そこで、 モンテカルロシミュレイションにより、二つのガウシャンの平均値と巾を評価 した。バルジの星は、 バーデの窓でのメタル分布(Zoccali et al 2008) とサルピータ IMF を持ち、 年齢は 10 Gyr と仮定して、 α 増強 BaSTI 等時線(Pietrinferni et al 2004) の内挿から、理論的光度関数を計算した。それを図5に示す。 この光度関数を、下の ΦRC(MKso)と背景 B(MKso) の和でフィットした。 log B(Kso) = a + b(Kso-13) + c(Kso-13)2 フィットの結果、 MKs, RC = -1.72, σKs, RC = 0.18, MKs, RGBB = -0.91, σKs, RGBB = 0.20 が得られた。レッドクランプの K 等級は太陽近傍から得られた -1.61 (Alves 2000, Laney et al 2012) より少し明るい。巾の方は太陽近傍(Alves 2000) と 一致する。RGBB のモデル値はレッドクランプより 0.81 mag 暗く、その相対数 は 20 % である。この相対値は I-バンドの値 (Nataf et al 2013)に近い。 フィットはあまり良くないが、関数形自体は太陽近傍での観測によく合い、 等時線の不定性からこれ以上の改善は難しい。 (背景成分の a, b, c について記述がない。MKs, RC について、 他の研究との比較はどうか?LMC, 太陽近傍での MKs, RGBB は?) ピーク巾を広げる 微分減光と測光エラーによる巾の広がりを評価する。 (微分減光"differential extinction" とは何か?区間内の減光の散らばりらしい。) そのため、減光マップの各ピクセル 毎に (J-Ks) カラーの標準偏差 σ(J-Ks) を求める。 (2.1.節で RC 星 200 個を含むという条件で決めた数分角の区分を指すと思う。) J-Ks の散らばりは次の 3種から起こると考える。 (i) σRC,JK = レッドクランプの固有カラー分散 (ii) σJ, σKs = J と Ks の測光エラー (iii) σA,JK = 残差減光 "residual extinction" (残差減光とは何のことかよく分からないが、上を読むと微分減光=区間内での 減光の散らばり "differential extinction" と同じ意味で使っているようだ。) |
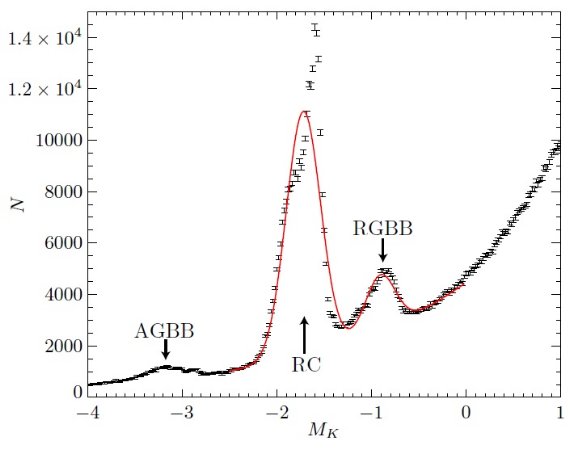 図5.バーデの窓でのメタル分布(Zoccali et al 2008) に (Pietrinferni et al 2004) の α 増強 BaSTI 10 Gyr 等時線と サルピータ IMF でモンテカルロシミュレーションを行った。赤=我々が 仮定した光度関数+フィットした背景。特徴的な個所に名前をつけた。 以上から、各ピクセル(= 減光を決めた数分角の区間)での残差赤化"residual reddening" は σ2E,JK = σ(J-Ks)2 - σ2J - σ2Ks - σ2RC,JK で求められる。2.1.節で述べたように、σRC,JK = 0.05 が低減光領域の観測から得られている。 σJ, σKs は DR1 カタログにある測光 エラーの平均である。 これらの結果、光度関数の固有ピーク巾 σRC(Ks) は 残差減光 σA,JK = AKσE,JK と測光エラー σKs により幅が広がる。 (上式のAK は、RK = (AK/E(J-Ks) の誤り?) これは固有光度関数と分散 σ2 = σ2Ks + (AKsσE,JK)2 の コンボリューションから作られる。 |
|
星計数式 視線方向の密度分布は、ルーシーリチャードソン法によるデコンボリュー ションを少し変えて求める。距離指数 μ = 5 log(r/10pc) を使うと、 星計数の基礎方程式は、 N(Kso) = B(Kso) + ΔΩ(ln10/5)∫ρRC(μ) ΦRC(Kso-μ)r3dμ さらに、Δ = ΔΩ(ln10/5)ρRC(μ) とおくと上式は N = B + Δ∗ΦRC となる。 ルーシーリチャードソン法 ルーシーリチャードソン法ではポアソンエラーを仮定する。N(Kso) のエラー はポアソンだが、 N(Kso) - B(Kso) のエラーはポアソンではない。そこで、 逐次近似式に以下のように変更を加えた。 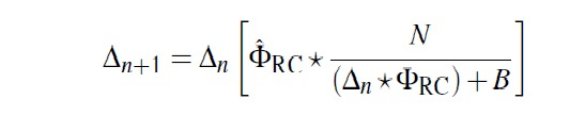 "adjoint" は良く知らないし、Φ(-M)の意味も何だろ?だが、ネットで 調べた限りでは、B = 0 の背景ゼロの場合は以下のようにあるのではないか。
B = 背景を加えると、以下のようにするということらしい。
N(K) には背景 B(K) が加わっているからつじつまは合う。問題と思うのは、 背景分は本当は固有光度関数の一部のはずなのに、本当に各領域で割り当て られた背景として扱われていること。まっ、いいか。 逐次近似回数の上限 デコンボリューションは間隔 0.02 mag で行った。スタートは Δ = sin2 = Hann 関数を使用。ルーシー・リチャードソン法では 逐次近似の回数を多くし過ぎると偽の高振動構造に辿り着く。そこで、 0.02 mag ビンで次の制限をクリアしたら近似を止める。 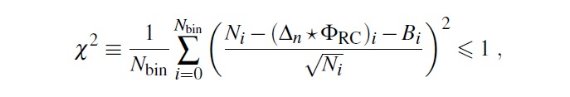 等級分布から距離分布へ(体積効果) 図7には得られた密度構造を示す。図6と図7を比べると、デコンボリュー ションの結果、遠いレッドクランプの数が減ることが判る。これは単純な体積 効果である。等級で等間隔にして数えると r3 に比例するから である。 |
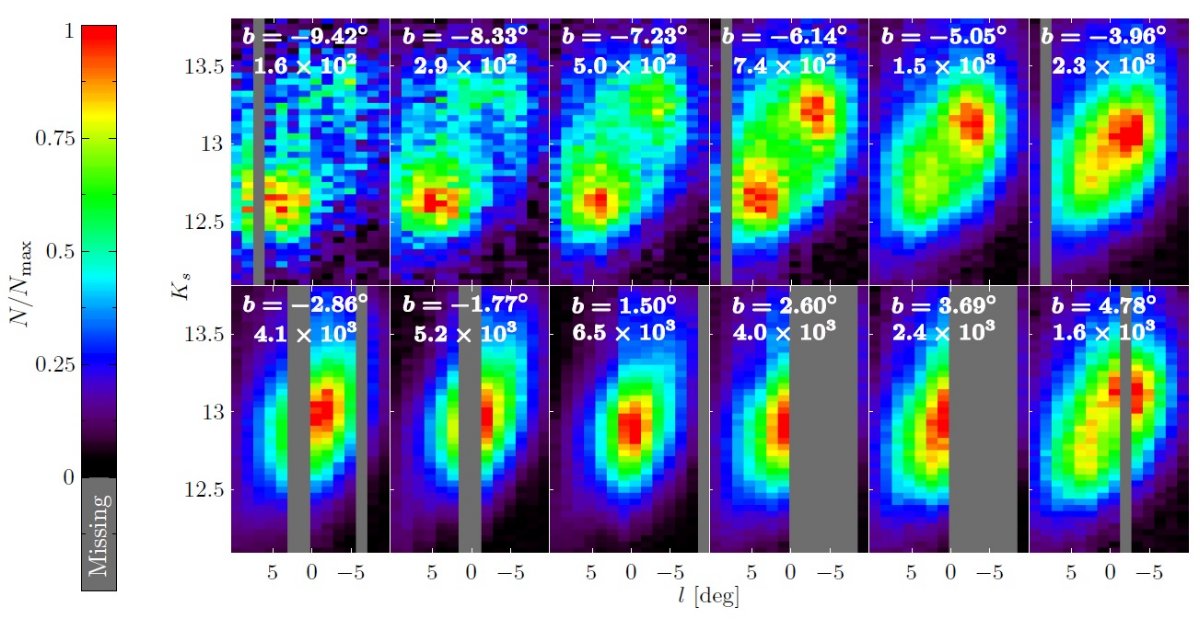
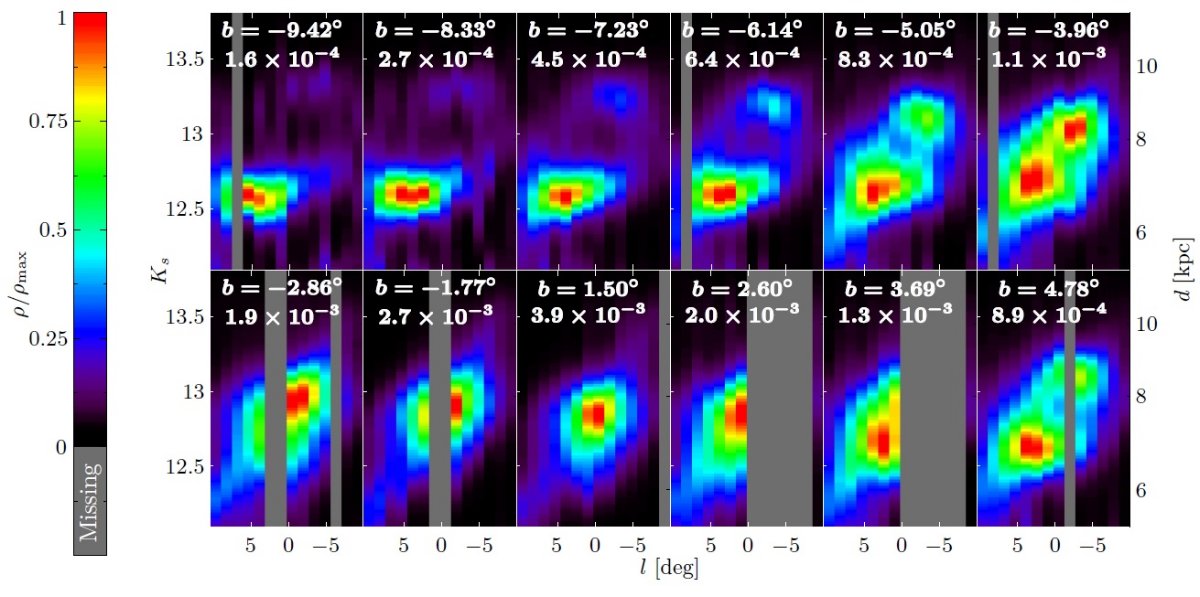
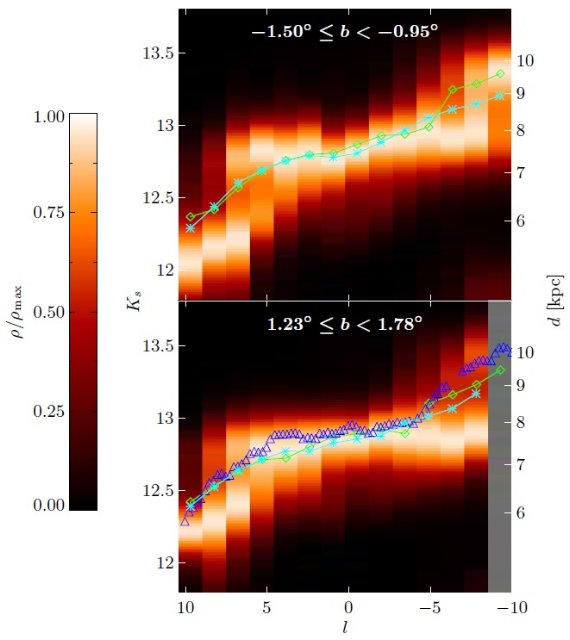 図8.デコンボルブした Ks-l 図。MK,RC = -1.72 を仮定。 緑菱形= Gonzalez et al. (2011). 青三角=西山その他 2005. 密度は最高密度 ρmax で規格化した。 シアンアスタリスク= Gonzalez et al 2011, 西山その他 2005 の 有効等級 ⟨Ks⟩ に変換した場合の密度(ピーク?) Gonzalez et al 2011, 西山その他 2005 との比較 結果の正しさを確認するため、図8には b = ±1 の2層で、 Gonzalez et al. (2011). と西山その他 2005 の結果と比較した。彼らのレッドクランプ位置は 視線方向密度分布の遠い側の崖際の位置する傾向がある。しかし これは体積効果、Gerhard, Martinez-Valpuesta 2012 の影響である。 Cao et al 2013 による以下の平均等級を最少して求めたピークを 図8に示す。これが両者のカーブを良く再現していることが判る。  |
|
8回鏡面対称の仮定 バルジの形状には3つの直交面に対する面対称性を仮定している。 その理由は、 (i) VVV DR1 がまだ不完全。 (ii) この仮定により、異なる等級の点の平均を出すので、光度関数と 背景の関数形に対する依存度を低下させる。 (iii) 仮定から等密度であるべき点の間の密度の差からエラーが評価 できる。 ("8-fold mirror symmetry" は間違った言い方ではないか?) 平均密度の計算 ρ(l, b, r) = 視線方向で得た密度分布。xyz 座標系を図9のように定義 する。x = バーの主軸に沿う。 z = 銀河北極方向。格子区間 Δx×Δy×Δz = 0.15×0.1×0.075 kpc を採る。ρ(l, b, r) を内挿して格子区間中央の密度とする。対称8点を平均 して ⟨ρ(x, y, z)⟩ とする。 主軸の決定 α = 太陽-銀河中心線と主軸との作る角。 Ro = 中心距離とする。 次に z = 一定面上で、二乗平均誤差 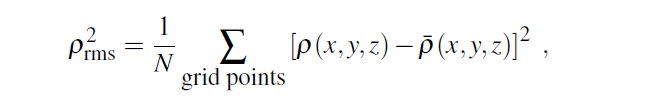 を計算する。そして、次の量を最小化して主軸を決定する。  ここに、⟨ρ⟩z = z一定面での平均密度、 ⟨ρrms⟩z = z一定面での平均二乗誤差。 |z| < 400 pc は除く。 |
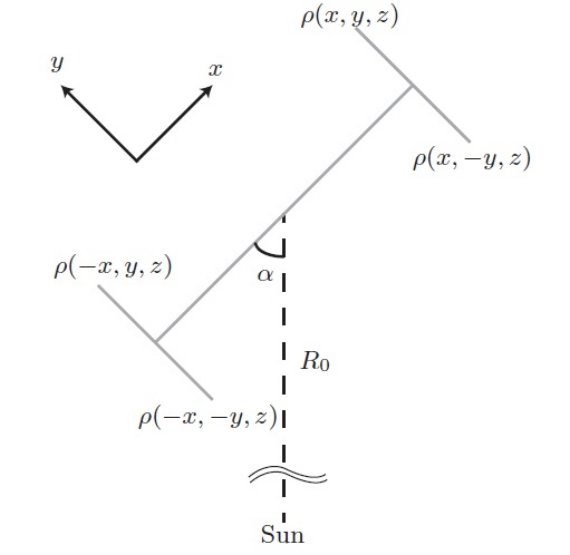 図9.銀河面北極から見た座標系。 |
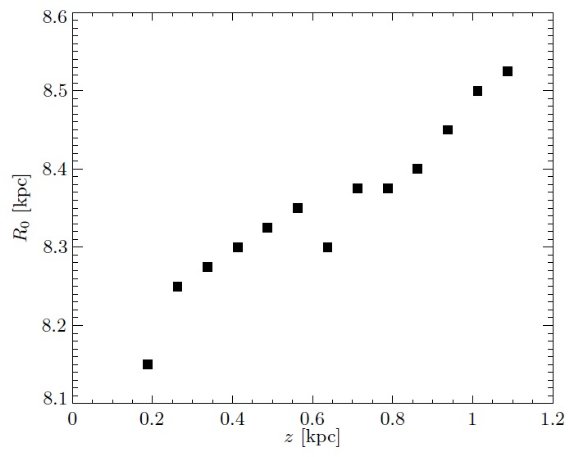 図10.各銀河面高度 z 毎に求めた Ro の変化。α = 26.5 固定。 Ro の決定には ρrms,z/⟨ρz⟩ の最小化 を用いた。尤もらしい説明はメタル量勾配の結果、レッドクランプ星 光度が変化するというものである。 Ro の決定 α は固定して、 Ro を z = 一定の層ごとに ρrms,z/⟨ρz⟩ の最小化 から決めた。図10には α = 26.5 に対する Ro の変化を示す。 メタル量勾配による説明 Gonzalez et al 2013 はバルジのメタル量勾配 0.28 dex/kpc を 得た。対応するレッドクランプ星の等級変化は dMK,RC/d[Fe/h] = 0.275 (Salaris,Girardi 2002)である。すると、レッドクランプの 等級は 0.09 mag 変化するであろう。これが正しければ、みかけ距離の変化は レッドクランプ等級がメタル量によって変化するためで説明可能である。 (等級が 0.09 mag 変化すると log r は 0.02 変化するから r が 0.02x2.43= 0.05 変わる。8 kpc x 0.05 = 0.4 kpc。) |
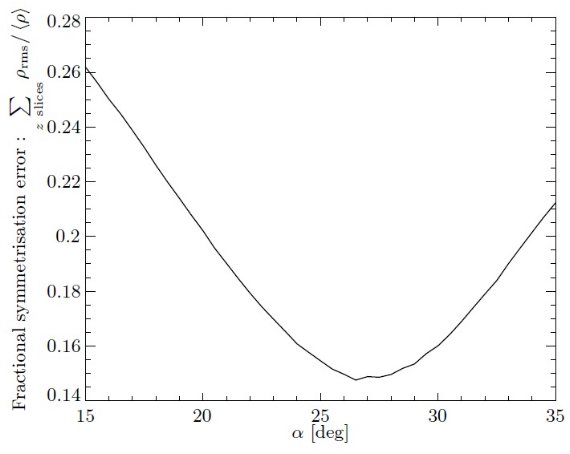 図11.軸方向 α によるフィット度の変化。 減光則の変化による説明 低銀緯では Nishiyama et al. (2006) の減光則より急で、銀緯と共に平坦になって行くという説明もあり得る。 この点、 Pietrzynski et al. (2003) や Laney et al 2012 の丁寧な解析からは dMK,RC/d[Fe/h] がゼロでないという証拠は得られなかったことは 重要である。 中心を同位置に動かす MK,RC のあり得る変化の補正を考える代わりに、我々は α を固定し、 Ro を各 z 毎に決め、バーを同じセンター位置に置き直す。これは Ro を固定して MK,RC を変えることに等しい。 図11には α によるフィットの変化を示す。α = 26.5 が 極小を与えることが判る。 こうして、この論文の最終結果にたどりついた。3Dマップ化作業は図12 に示した。図12から、仮定した3軸極鏡面対称が妥当であることが判る。 |
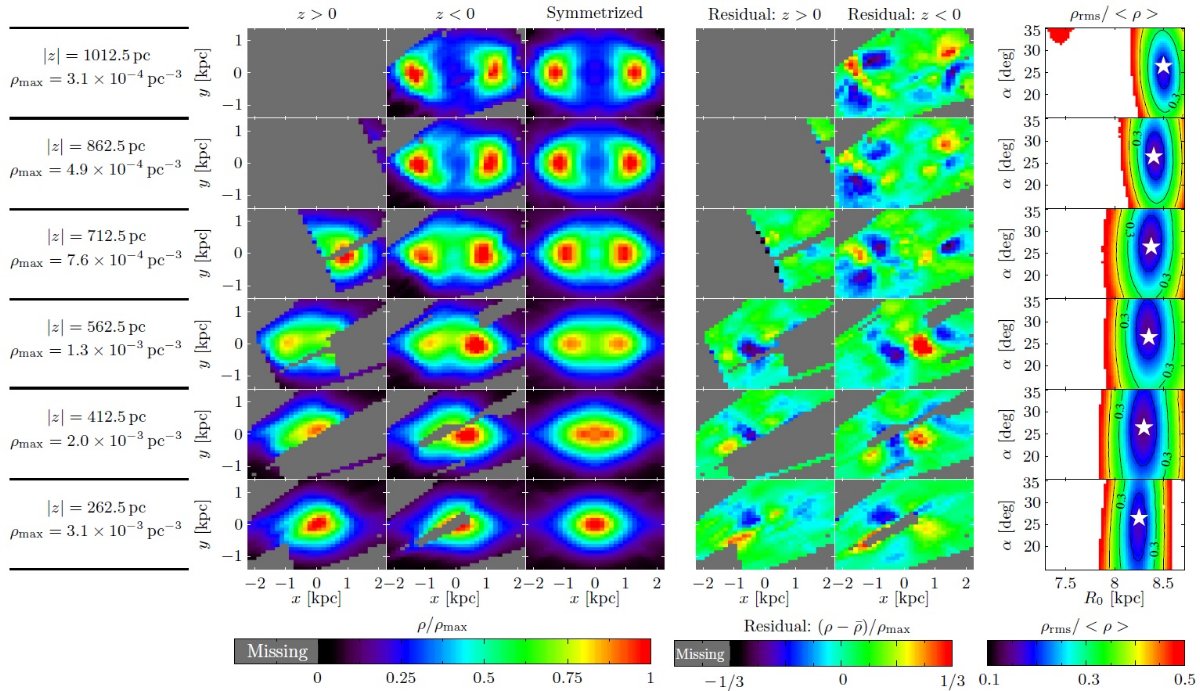
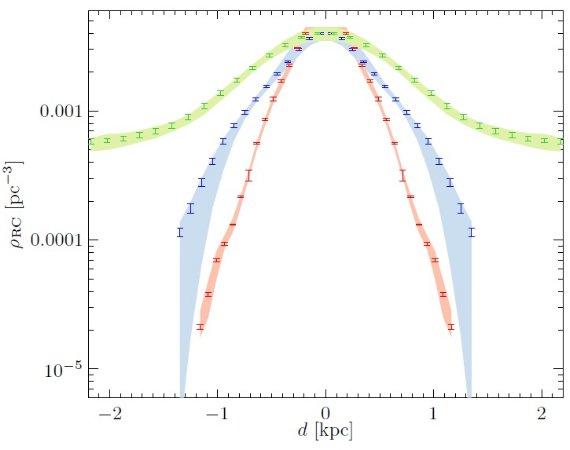 図15.緑=主軸に沿ったレッドクランプ星の密度変化。赤=短軸沿い。 青=中間軸沿い。主軸と中間軸は銀河面から 187.5 pc からずれている。 エラーバーは対称化に伴う内部エラー。影=第6章で述べた密度範囲に対応 する系統誤差。 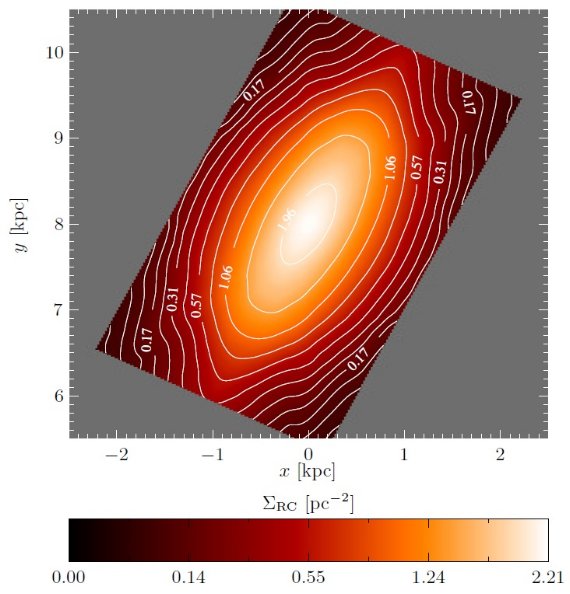 図17.銀極から見たバルジ。数字はレッドクランプ星 pc-2/sup> である。銀河中心から 150 pc 以内は信頼度が低いので外した。 X−形 図19ではバルジを y-軸方向、真横から見た図18の表面密度を異なる 高さ z で切った断面密度を示す。|z| ≥ 0.5 kpc で強い X-型の形 が分かる。 |
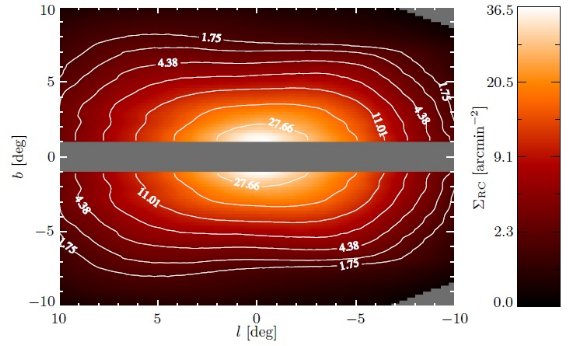 図16.太陽から見た時の投影図。Ro = 8 kpc を仮定。 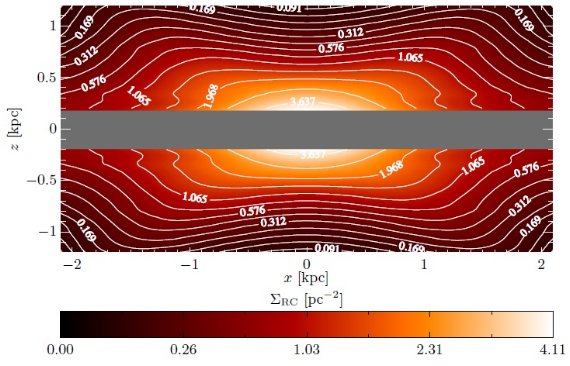 図18.中間軸に沿った投影図。数字はレッドクランプ星 pc-2/sup> 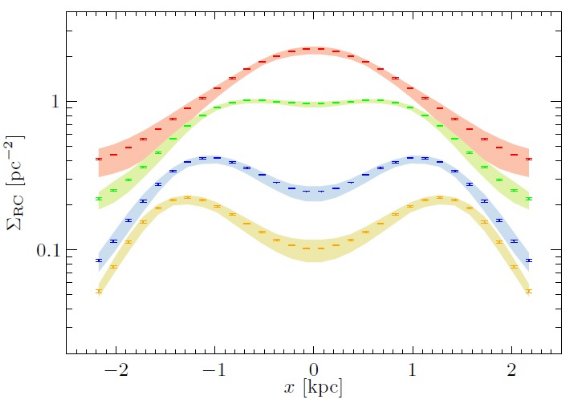 図19.図18の横からの表面密度の一定高度(z)での密度プロファイル。 赤:z = [0.15, 0.45] kpc. 緑:z = [0.45, 0.75] kpc. 青:z = [0.75, 1.05] kpc. 黄色:z = [1, 1.2] kpc. |
|
これまでの仕事 これまでのバルジ密度分布は、 (i) パラメタ―フィット。Dwek et al 1995, Rattenbury et al 2007, Cao et al 2013 (ii) ノンパラメトリックに表面輝度分布をデプロジェクト。 Binney et al 1997, Bissantz, Gerhard 2002. (iii) レッドクランプより明るい星計数を逆変換。Lopez-Corredoira et al 2005. 箱/ピーナツ型形状 しかし、レッドクランプはより良い標準光源である。得られたバルジの 3次元密度分布はボクシー/ピーナツ型構造を示した。 定性的には N-体シミュレーションとよく似ている。 |
スケール長 図15の [0.4, 0.8] kpc で決めたスケール長は長軸 0.7 kpc, 中間軸 0.44 kpc, 短軸 0.18 kpc で軸比 10 : 6.3 : 2.6 であった。 しかし、短軸はピーナッツ形状のため全体を楕円体でフィットした時より も短く出ることに注意せよ。 バックリング 対称化以前の図12、図7を見ると分かるが、銀河中心が現在 バックリングを経験中 Athanassoula 2008 ということはなく、現在は バックリング後の修復過程期と看做すべきであろう。 |