A Model of the 8 - 25 Micron Point Source Infrared Sky

　アブストラクト

　２．銀河系　

　２．１．銀河系構造要素　

IRAS 等級　 [12] = 4.034 - 2.5 logF(12) [25] = 2.444 - 2.5 logF(25) [60] = 0.490 - 2.5 logF(60) 　円盤　 Bahcall, Soneira 1980 の二重指数関数モデルを採用し、ρ = 数密度、S = スペクトル型として 　　　　　ρ(R, z, S) = ρD exp[-(R-Ro)/h -|z|/ hz(S)]　　　R ≤ Rmax 　　　　　　　　　　= 0　　　　　　　　　　　　　　　　　　　　　　　 R > Rmax 　我々のモデルは h の値にあまり影響されないので h = 3.5 kpc とする。 ただし、 hz は表２に示す星クラス毎に違い値を与えた。例えば、若い星には hz = 90 pc, 最も古い星では hz = 325 pc である。 Habing 1988 は IRAS 天体の分布モデルにかなりの量の厚い円盤成分を必要とした。しかし、 我々のモデルにはそのような成分は必要でなかった。我々のモデルでは |b| が小さい、腕やリングが大事な所、バルジが強い GC 付近を 除いて、円盤成分は最重要である。 　バルジ：軸対称！　 Bahcall 1986 の提案した表式を採用した。バルジ軸比を k1 = a/b > 1 として、 　　　　　ρ(x, S) = ρB x-1.8 exp(-x3) 　　　　　x = sqrt(R2 + k12z2) /R1 　ハロー　 楕円銀河の表面輝度 I は下の式で表される。 　　　　　log[I(α)/I(1)] = -3.3307 (α1/4 - 1) 　　　　　α = sqrt(R2 + ke2 z2)/Re ke = ハローの軸比。Re = ハロー有効半径。光度の半分 は α = 1 以内から来る。 　腕　 　腕密度の R 方向とｚ方向分布は円盤と同じ形を採用した。腕の巾は R 方向に 750 pc でその中心軸は下の式で表される。 　　　　　θ(R) = α log (R/Rmin) + θmin

表１．渦状腕のパラメタ― 表１には Georgelin, Georgelin 1976 の４本腕をなぞるパラメタ―が選ばれた。 Elmegreen 1985 には２本腕と４本腕を比較したよいレビューがある。 局所腕　 　局所腕は HI (Weaver 1989), CO (Cohen et al 1980), 大質量星 (Becker-Fenkart 1970, Weaver 1989). 　分子リング　 　CO 観測 Clemens, Sanders, Scoville 1988 は R = 0.45 Ro に分子リングの存在を示した。Volk et al 1992 はその位置に IRAS 天体の超過を見出し、IRAS 天体の銀河系モデルにリングは不可欠とした。 リングまでの距離が遠いため、彼らは主に赤外で明るい高質量天体をモデルに 含めた。IRAS が検出できるのは非常に明るいリング天体に限られるからである。 しかし、Eaton et al 1984 は K 星計数からリングにはもっと暗い星が含まれて いることを示した。その意味で、「分子リング」は「恒星リング」と看做せる のである。銀河にはリングを有するサンプルが多数ある。 リングの密度分布は、ガウス型で、 　　　　　ρ(R, S) = ρr(S) exp[-(R-Rr) 2/2σr2] リング半径 Rr = 0.45 Ro, σr = 0.064 Ro である。 これは半巾 0.15 Ro に相当する。また、ρr(S) はクラス S の星 が R = Rr で持つ密度である。リング星のスケール高は円盤星と同じと 仮定する。

　２．２．天体テーブル　

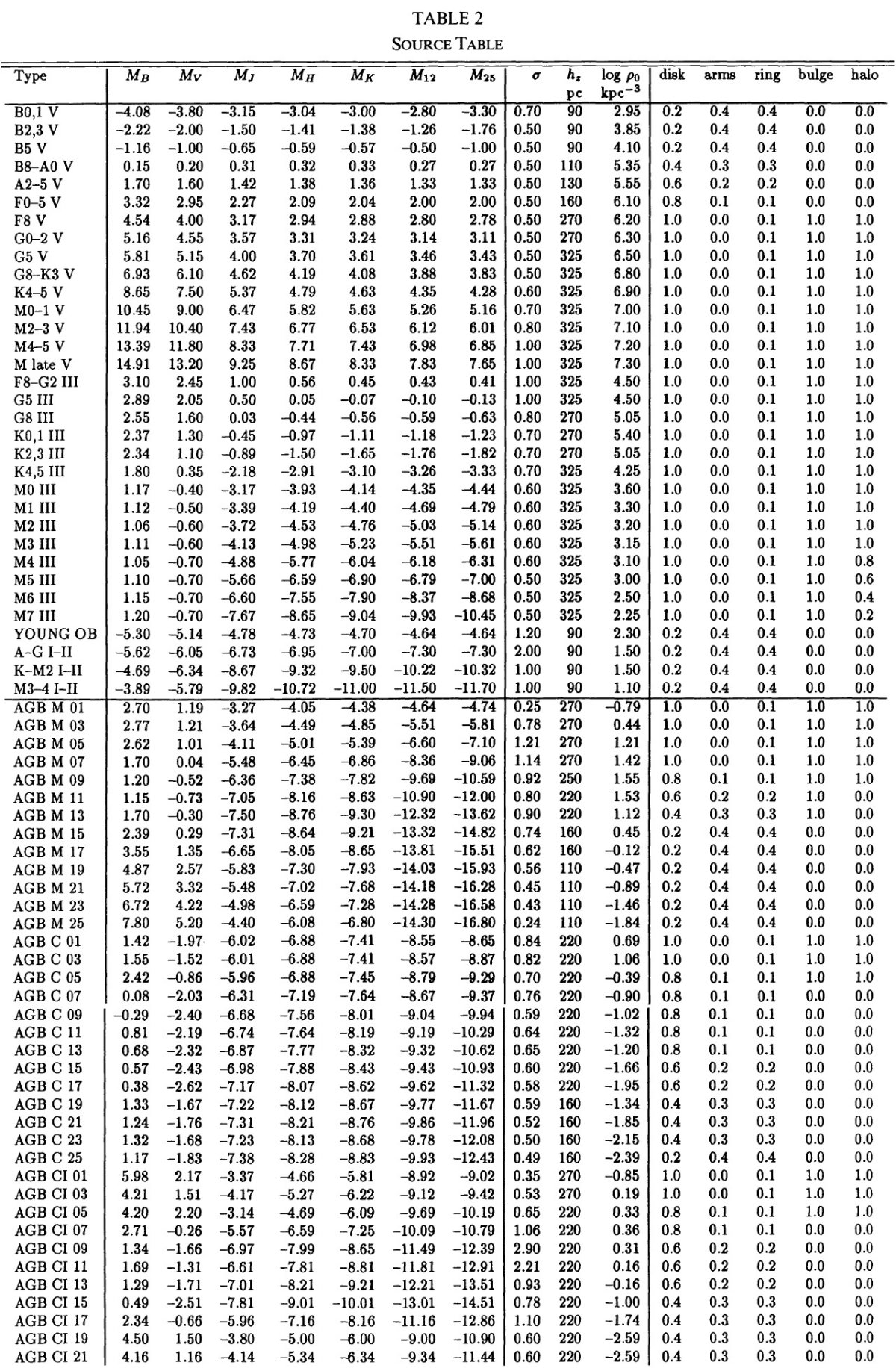
図１a． 　天体分類　 　テーブル作成の原理は Elias 1978, Jones et al 1981, Garwood, Jones 1987 と同じである。彼らは恒星クラスにまで分解して光度関数を表現した。各クラスは そのバンド毎の絶対等級、その散らばり、太陽近傍での数密度、円盤スケール高、 銀河系上述の５成分に属する相対比で特徴づけられる。各クラスは次の形の等 級分布を持つとする。 　　　 N(M) ∝ exp [-(M-Mλ)2/2σ 2] この絶対等級 Mλ は色々な文献からの寄せ集めであり、 基準とされるべき性質の物ではないので注意して欲しい。 　２．２．１．星テーブル　 　通常星の区分　 　表２には８７種類の銀河系天体を載せた。表の最初は Jones et al 1981 と よく似ている。そこには　３３種の正常星が載っている。Jones et al 1981 と の違いは F8 - G2 V 星を F8 V と G0 - G2 V の二つに分けたことである。 これはモデル V 光度関数を観測 V 光度関数により合うようにするためである。 さらに、低質量赤色矮星を表現するため、 晩期 M V 星を加えた。そして M8+ V 星は除いた。このクラスはマスロスを伴う進化した星で、 IRAS では非常に重要 である。これ等の星は表２の第２部で扱われる。 　表の第１部　 　第１部は基本的に Elias 1978a, Jones et al 1981, Ruelas-Mayarga 1986, Garwood, Jones 1987 から採った。V-K, J-H, H-K は Elias が採用した Johnson 1966 でなく Koorneef 1983 を採用した。Mv は様々な文献、Blaauw 1963, Keenan 1963 その他 Elias 1978a に載っている、から採った。[V-12], [V-25] は Cohen et al 1987 を採用した。ただし、K III と K V 星の [V-12], [V-25] は少し青すぎるので赤くした。Jpnes et al 1981 のスケール高よりは少し大きい Bahcall, Soneira 1980 の値を使った。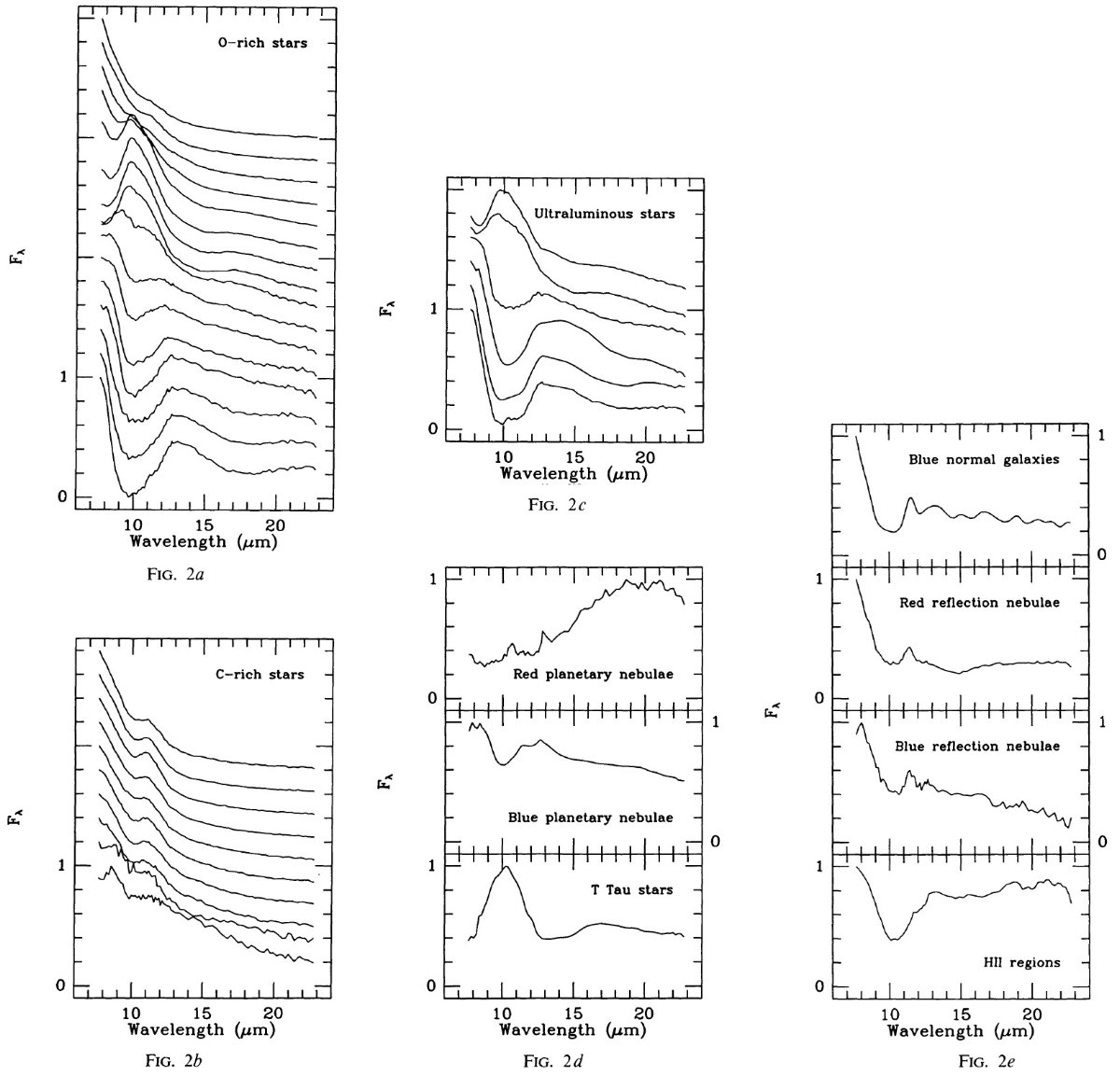 　表の第２部　炭素星　 　次は進化した AGB 星で様々な程度でダストシェルに覆われている。 表は O-リッチと C-リッチ星に分かれる。炭素星はさらに可視炭素星と赤外 炭素星に分かれる。それらの M12, M25, ρo 値、散布度は 1.25 - 8 Mo の 進化計算(付録)に基づいて決めた。炭素星に成るのは 1.25 - 4 Mo の星である。 夫々のクラスが特定の [12-25] カラーを有する。例えば、"AGB M 07" は O- リッチで [12-25] = [0.6, 0.8] であり、表では [12-25] = 0.7 とされる。 炭素星の近赤外カラーは Claussen et al 1987 の表を利用した。 [K-12] > 2.4 の炭素星は赤外炭素星に分類した。B,V 等級を Stephenson 1973 のカタログからとりそれに Claussen et al 1987 の Av で赤化補正した。 [12-25] が大きな炭素星では可視等級が得られない。それらには推定値を充てた。 　表の第２部　M-星　 　M 星では GCVS の LRS = 2n, 3n 星、と AFGL の非常に赤い M-星を選んだ。 そして [12-25] の各区分毎に [K-12], [V-K], [B-V] を定めた。B 等級は Bright Star Catalog と SAOC から採った。V 等級は BSC, SAOC, IRC, K 等級は IRC, Gezari, Schmidt, Mead 1987 から採った。それらの値が得られない [12-25] カラーの星は外挿を使った。 　空間密度　 　AGB 星の相対密度は星進化モデルから決める。絶対等級と散布度も同様である。 最終的な空間密度は 12 μm 合成総光度関数 M12 = [-14, -11] を Volk et al 1992 の数値光度関数に規格化して決める。 　第３部＝超高光度 12 μm 天体　 　ここでは、M12 < -17 をそう定義する。OH/IR 星の内 46 星がこのカテゴリーに入る。さらに文献で他のタイプの星で M12 < -13 を探した。かなり多数の天体が候補に上がったが、運動距離以上には 確実な距離が得られない。距離がよく決まった星としては、LMC の Hubble- Sandage 天体 S Dor と R 71, 明るい M 型超巨星 S Per, M-型 hypergiants VX Sgr, VY CMa, B1 hypergiant MWC 300, 特異天体 η Car. 全て M12 = [-18.1, -13.5] の範囲内である。これ等の天体を表２で Xn として表示した。 X1E はシリケイト 放射、X1A はシリケイト吸収の星である。それらの数密度は Volk et al 1992 （発表なし？）の光度関数に合うように定めた。 　第４グループ。 　第４グループは T Tau 星である。そのスケール高は 90 pc とした。彼らの 速度散布度 2 - 3 km/s と年齢 10 - 30 Myr から、 T Tau 星の分布は母分子 雲から数十ｐｃ広がることが判る。T Tau 星の (B-V)o, Mv は Taurus-Auriga 雲の Herbig-Bell カタログ(1988) から求めた。(J-H)o, (H-K)o は Rydgren et al. 1989a を使った。M12 も Taurus-Auriga 雲データから求めた。 空間密度を求めるため、 M ≤ 3 Mo の主系列星は全て T Tau 期を経る、その 期間は Mcore ≤ 1 Mo 星で 30 Myr とする。Mcore > 1 Mo 星では T Tau 期間は Iben 1965 の "point 8" に達するまでとする。各質量に対し、その主系列星 空間密度に （T Tau 期/主系列期）を掛けて T Tau 星空間密度とする。 各質量区間毎に空間密度を決め、総計すると ψ = 3.7 104 kpc -3 になる。 　２．２．２．非星グループ　 　第５グループ＝星雲　 　第５グループは惑星状星雲、反射星雲、 HIIRs を入れた。HIIRｓのスケール 高は若い種族の値を使った。反射星雲は少し大きな値、惑星状星雲は巨星と 同じ値を使う。近赤外等級は Whitelock 1985 を、可視等級は　Acker, Marcout, Ochsenbein 1981 のカタログから採った。Walker et al 1989 に倣い、 「赤い」と「青い」惑星状星雲に分けた。「青い」惑星状星雲は [12-25] = [1, 2.7], [25-60] = [0.7, 3.5] とした。距離が知られている惑星状星雲を 調べた結果、「青い」惑星状星雲は M12 = -11 より明るく、 全星雲の 5 % を占めることが判った。 IRAS は 1 kpc 以内に 30 惑星状星雲 を検出した。これは 1 kpc 以内星雲の 40 % に当たる。その他の星雲は年齢が高 過ぎて IRAS 波長では暗すぎてしまうのである。この数字から、スケール高 250 pc を仮定して、数密度 19 kpc-3 を得る。 　反射星雲は中心星の同定を nan den Bergh 1966, Herbst 1975, van den Bergh, Herbst 1975 から得た。我々は自身で DM を決定し、M12 を得た。 反射星雲も「青い」 [12-25] = [1.1, 2.3], [25-60] > 3.0 と「赤い」 [12-25] ≥ 2.3, [25-60] > 2.0 に分かれる。 N(D)/D2 をプロットすると、反射星雲サンプルは 500 pc 以内で 完全と推定される。スケール高 = 120 pc として密度を決めた。 　同じ方法で HIIRs も扱った。データは Reifenstein et al 1970 と Wilson et al 1970 から得た。距離は電波再結合線視線速度から決めた。 IRAS は 1 kpc 以内で完全サンプルであることが判った。そこから [12], [25], 空間密度を決めた。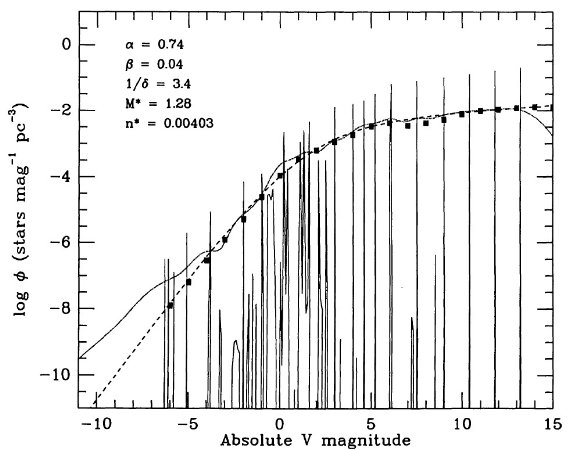 　２．２．３．光度関数　 　図１a: V バンド光度関数　 　図１a: では V バンド光度関数を Bahcall, Soneira 1980 と較べた。彼らのは太陽近傍の光度関数であるので、腕間空間の性質上 若くて明るい天体を欠く。我々は全銀河で合わせる目的がある。

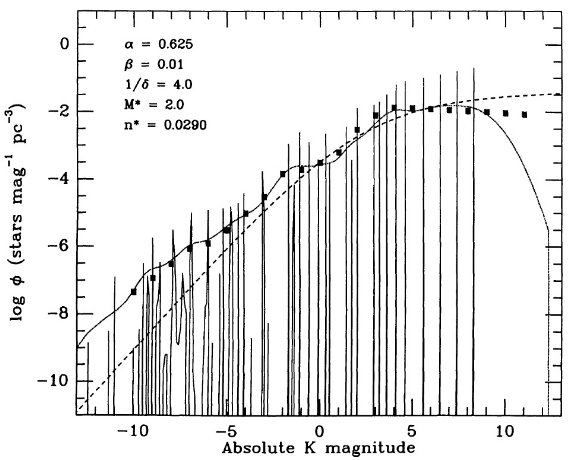
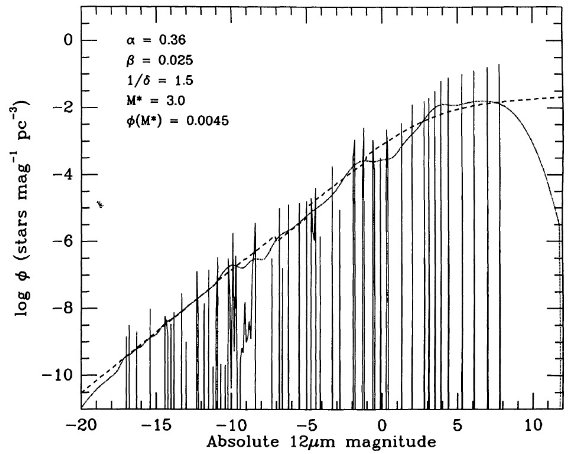
図１b． 図１c． 　図１b: K バンド光度関数　 　我々のと Eaton et al 1984 を比べた。使用データがほぼ同じなので 大体同じ光度関数が得られた。 　図１c: 12 ミクロン光度関数　 　我々のと Volk et al 1992 を比べた。

　２．３．LRS スペクトル　

　２．４．星間減光　

Rieke, Lebofsky 1985 減光則　 　 Rieke, Lebofsky (1985) は銀河中心付近の明るい早期型星を用いて 8 - 13 μm の減光則を導いた。 これを全波長帯に拡張するため、我々は VI Cyg No.12 (B5 Ia)の LRS データベース からこの星のスペクトルを抜き出した。 我々はこの星の４つの独立したスペクトルの平均を調べた。しかし、このスペクトル を赤化補正しても黒体スペクトル、特に B5 Ia に対応する 14000 K のには ならない。星周フリーフリー放射が汚染しているのではないか？ 　シリケイト吸収星　 　そこで、この星はあきらめ、[12-25] = [1.05, 1.15] の 401 天体の平均 と、[12-25] = [3.0, 3.2] の 1 天体のを比べる。 前者は10, 18 ミクロンに薄いシリケイト放射帯を示す。後者は10, 18 ミクロンに 吸収帯を持つ。 二つのシリケイト帯の中間部の連続光をスプライン内挿して、 非シリケイト吸収を除去する。 (内挿じゃなくて外挿に見えるが？ ) そして残った 10 ミクロンでの超過放射と超過吸収を Rieke, Lebofsky 1985 の １０点をスプラインフィットして得たプロファイルと比較する。我々の超過放射の 方は RL 則よりずっと狭い。一方超過吸収は良く合っている。そこで、吸収帯 を示す星から決めた吸収帯を星間減光のシリケイト成分と看做す。 　吸収帯外側の連続減光　 　吸収帯外側の連続減光には、A(8μm) = 0.020 Av を起点にして、λ -1 則を仮定する。それによると A(25) = 0.005 Av である。 結果を図３に示す。 ( 星周ダストの減光を星間減光に使っているように見えるが。一応 " represent the silicate aspect of interstellar extinction" と 断ってはいるが、実際にはそれを星間減光に使用している。 使った星は一つだけのように見える。天体名が不明。) ( 右の 0.6 mag/kpc は小さ過ぎないか？)

図３．LRS 波長帯における星間減光則。 星間減光　 　ダストは二重指数関数型の分布を仮定する。距離 D - D+δD 区間 での減光 δAλ(R, z)は, 　　　δAλ(R, z) = Aλ, 0 exp[-(R-Ro)/hd - |z|/hd, z]δD　 R < Rmax 　　　　　　　　　　　= 0　　　　　　　　　　　　　　　　　　　　　 　　R ≥ Rmax AK, 0 = 0.07 mag/kpc, AV, 0 = 0.62 mag/kpc を 仮定する。Jones et al 1981 は減光スケール長 4 kpc を得ており、星の 値に近いので採用する。hd,z = 100 pc とする。

　減光式はどうやって作ったか分かったので打ち止め