|
CRL 2688 の F606W/WFPC2/HST 撮像を行った。2対の「サーチライトビーム
」がダスト繭から上下に伸びているのを見つけた。ビームは想定される中心星
位置で交差している。アークの形は現行モデルで想定される極方向に伸びた形
でなく、ほぼ円形であった。 画像から過去 13000 年のマスロス史が導き出せる。表面輝度は r-3.7 で落ちて行く。これはマスロス率が r-0.7 で 低下することを意味する。 | マスロスには 150 - 450 年間隔でファクター2の 盛り上がりが 75 - 200 年続く。「サーチライトビーム」の縁と、星雲内側 1".5 < r < 6" の奇妙な構造を分解できた。今回のデータは新しい モデルを必要とする。ビームはダスト繭内にある一対の非直線状の環状の穴を 通って、放射される。穴は 200 年以内に高速流により作られ、その穴を抜けた高速流が周囲の濃い AGB 星風と相互作用して内側星雲を作った。コクーンの ダストは 0.6 &mu:m で広がった星雲内のダストよりずっと大きい。 |



|
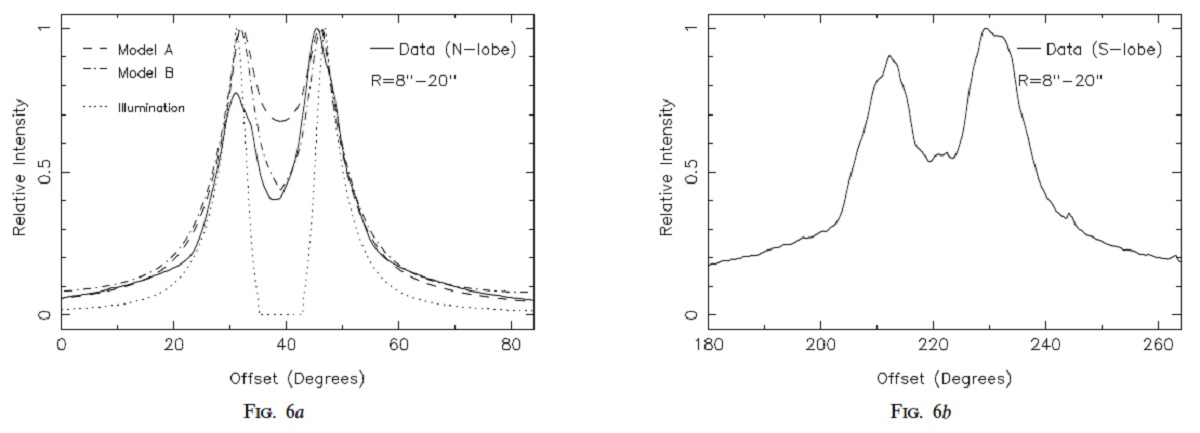
新しい特徴 2対の「サーチライトビーム」が見える。それを横切ってアークも見える。 それらの明るい部分は地上観測 Latter et al. (1993) と Crabtree, Rogers (1993) でも微かに見えた。 中心星位置 ビームの交点として (α, δ)2000 = (21h02m18s.27, 36°41'37".0) を得た。 |
アーク 最も遠い星雲光は 24.4 mag arcsec-2 レベルで、北側 51" に 見える。距離 1 kpc を仮定するとこれは 7.6 1017 cm である。 これに対し、地上観測の Latter et al. (1993) では、 27" までしか見えない。 マスロス時間変化 星雲がどこまで広がっているかは、逆二乗の場合マスロス量がサイズに比例 するから重要である。ただ、後に述べるがマスロスは時間と共に増加している。 |
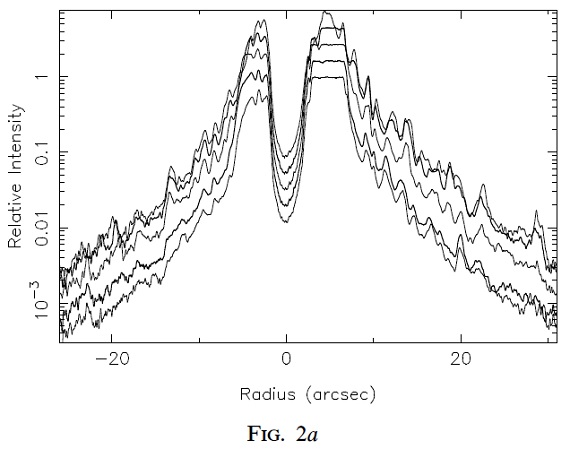 図2.(a): GRL 2688 中心を通る l = 31° - 212° 幅 14° の 動径方向強度変化。強度ピークで規格化してから、見やすさのため縦に ずらした。アークは小さなピークとして現れる。 形状 アークは円形であるが、赤道に近づくにつれ淡くなり、消える。照射光 が無くなるからであろう。アークはおそらく薄い3次元球形シェルがリム ブライトニングで円形に見えるのであろう。 マスロスの盛り上がり したがって、実際のシェルの厚み はアークの巾の 1/1.5 - 1/2 で、0".5 - 1".2, 距離 1 kpc として、実長で 0.75 - 1.8 1016 cm = 500 - 1200 au である。速度を 20 km/s として、マスロスの盛り上がりは 75 - 200 年間続いたと考える。 星雲の大きさを使うとマスロス期間は (7.6 1017 cm)/(20 km/s) = 12,000 年である。最も明るいアーク間の間隔は 0".6 - 1".8 なので、 150 - 450 年に当たる。 動径方向の断面 図2a には動径方向の断面を示す。正方向が北部分、負方向は南部分である。 |
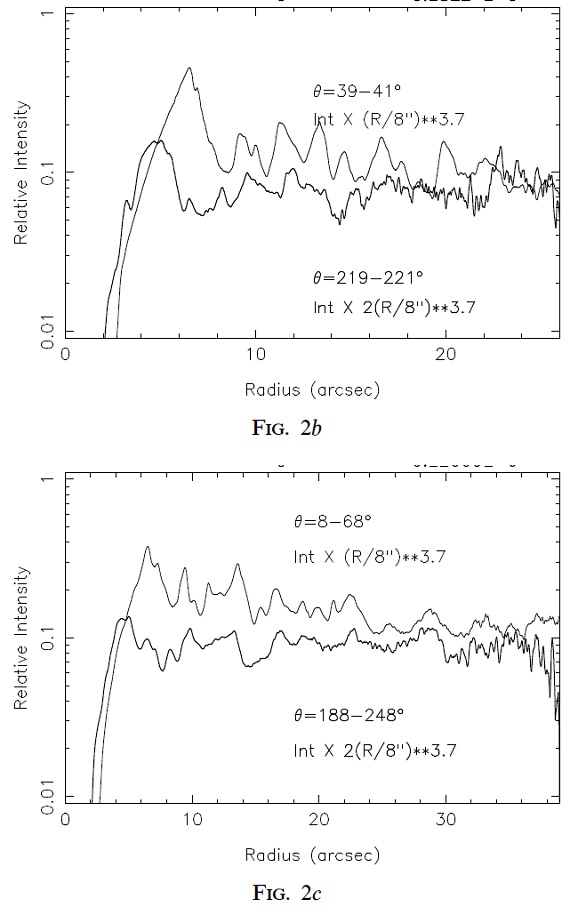 図2.(b) 反対方向のビーム、 θ = 39 - 41 と 219 - 221、 を重ねて比較。r3.6 を掛けて平坦化した。 (c) 緯度方向で平均した輝度の動径に沿った分布、r3.6 を掛けて ある。緯度平均の際に赤道近くは除いた。 |
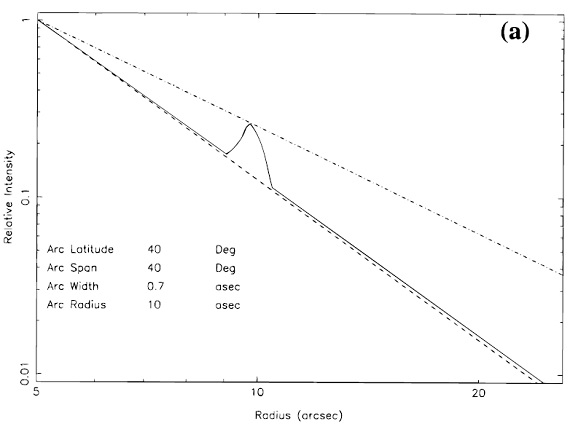 図3.(a) ρ ∝ r-2 モデルからの散乱光強度。 中心星からの照射光が緯度と共に増加。破線 r-3 と 一点破線 r-2 は参考のため。 ファクター3の局所密度の増加をアーク部のモデルとして加えた。 モデルの光学的深さはアーク付近で 0.1 とした。実際の CRL 2688 では数倍大きいだろう。 モデル ρ ∝ r-α の密度分布に対して散乱光の輝度分布 S(r) ∝ r-(α+1) である。Tamura88. 図3には単純な計算 Morris81 で, S(r) を求めた。 観測勾配から α = 2.7 観測では、r > 9" の散乱光分布は r-3.7 である。つまり 密度分布は r-2.7 に近い。これはマスロス率が距離と共に低下 することを意味する。時間と共にマスロス率が強化されるという結論は Yamamura96 とも合う。 総質量 ro = 10" から先の総質量は (dM/dt)o (rmax0.3ro0.7/V) は 0.7 Mo である。これから Mms = 1.3 Mo が予想される。 もし仮に、マスロス率が (dM/dt)o で一定のままであるなら。散乱光星雲の質 量は 2.1 Mo となり、 Mms = 2.7 Mo になる。注意しておくと、星雲の外径が もっと大きくなるとこの質量は大きくなる。 |
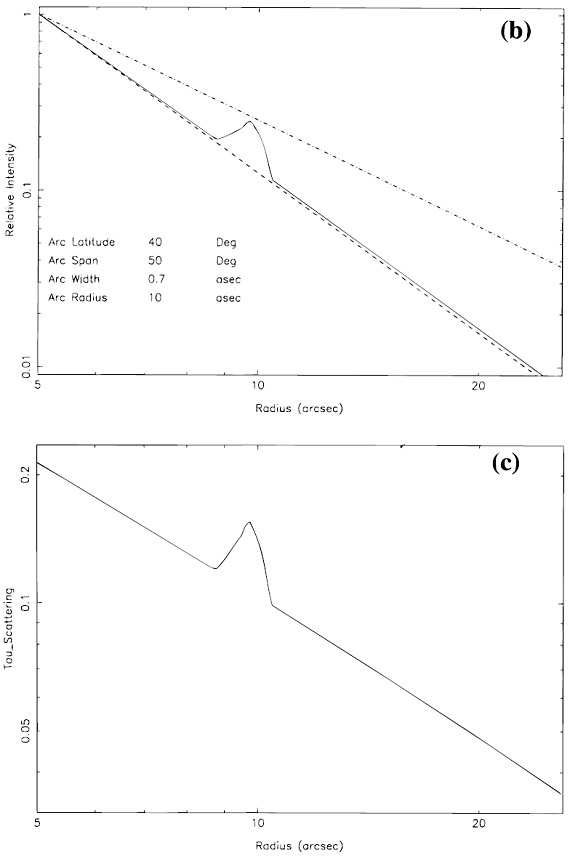 図3.(b) ρ ∝ r-2 モデルからの散乱光強度。 中心星からの照射光が緯度に無関係で一定。破線 r-3 と 一点破線 r-2 は参考のため。 (c) 視線方向沿いの光学的深さ。 |
|
YMW モデル Yuzef-Zadef, Morris, White 1984 の YMW モデルでは、円盤密度が赤道面 からの緯度に応じて低下して行き、θ > 80° ではゼロとなる。 このモデルは多くの双極型反射星雲の説明によく使われる。 CRL 2688 では合わない しかし、我々の観測はこのモデルと合わない。YMW モデルではサーチライト ビームは出現しない。また、散乱星雲の形は紡錘型にならない。 |
図4.破線=サーチライトビームを横切る断面に沿った強度の角度変化。 F606W WFCPC2 による。実線=Yuzef-Zadef, Morris, White 1984 YMW モデル による多重散乱モンテカルロコードの結果。大きな差がある。 |
|
輪形の穴 CRL 2688 の形態は星雲ダストを照らす光の非等方性に起因すると考える。 星の光が、それを取り巻く平たいダスト繭に開いた円環状の穴=annular hole を通って逃げ出し、星雲ダストを照らすのである。穴の形は円形でなく、輪形 で、その中央部がサーチライト中間部の暗い影を産み出す。繭は少し傾き、 南側の縁が我々に近い。 穴の成因 高速流がよろよろと回るために輪形の穴が切り裂かれたのであろう。 (歳差のことか?一本の高速流が穴 を明け。その跡を通って円錐壁状に光が放射されたのか?高速流も今は円錐壁 状なのか?サーチライトビームの分光は? ) 散乱光学的深さ また式がファクター2違う。どうしてかな? |
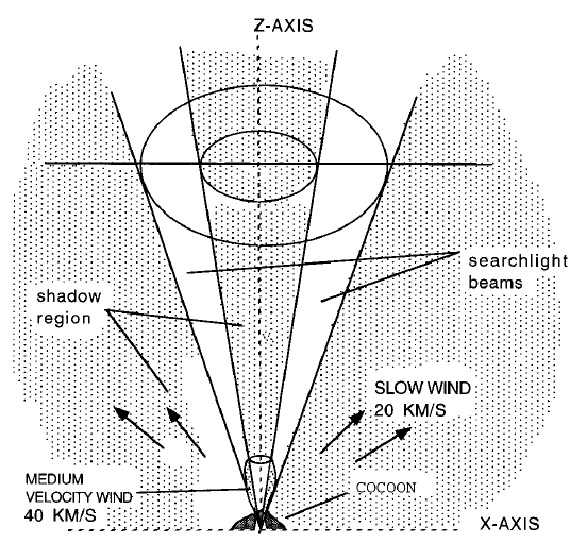 図5.新しい円環ホールモデル |