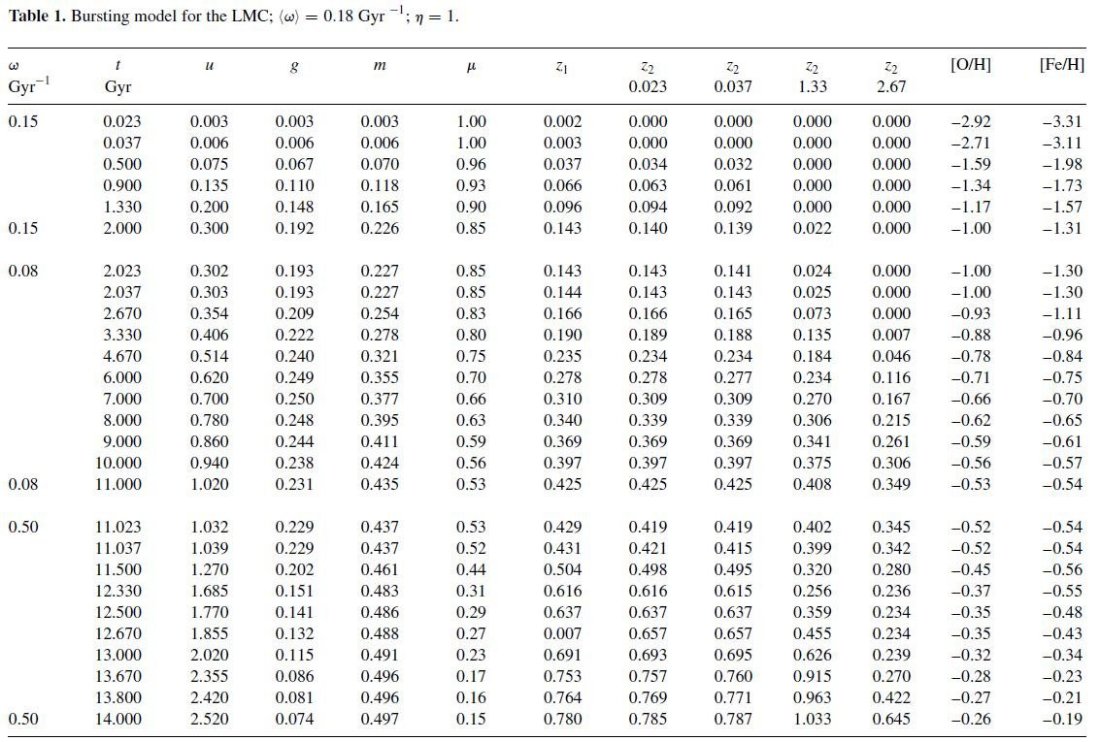
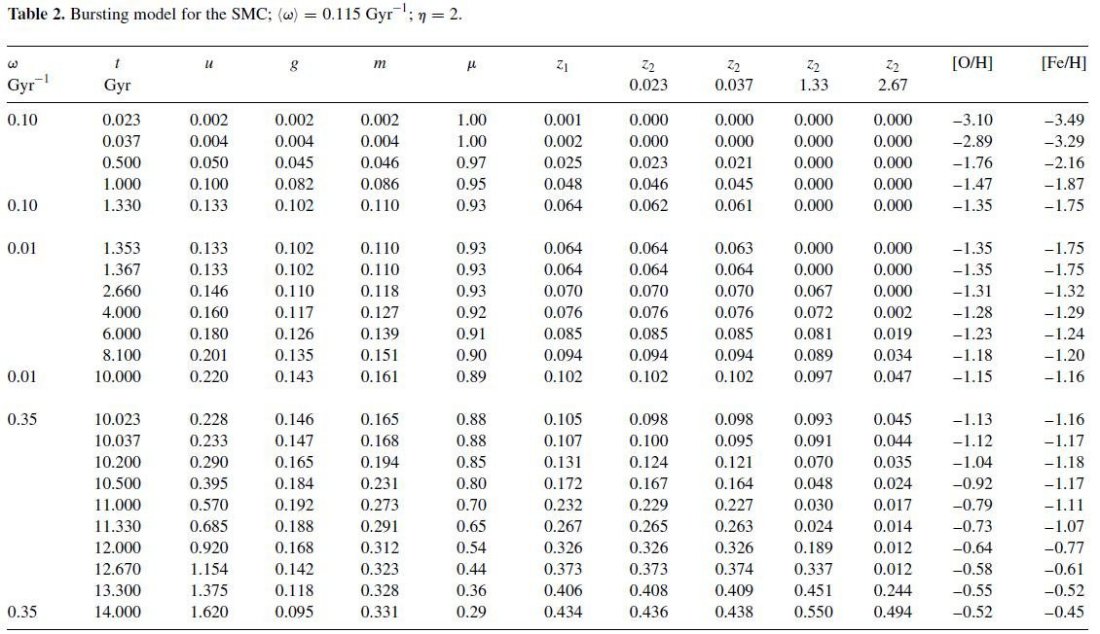
式 (1) - (11) の結果は表1,2の初めの7列に載せてある。図1,2は スムーズモデルとバーストモデルの星形成史を示している。LMC と SMC とで バーストの時期が大雑把には一致しているのはバーストが相互作用の結果生じた ことを暗示している。LMC に関し我々が仮定した η = 1 は Pilyugin 1996 と合っている。現在の星形成率は大体平均値に等しい。これは Westerlund 1997 が Hα 放射から導いた、二つの銀河の現在の星形成率は過去の平均を下回る、 という結論と較べられるべきである。このように、過去 3 Gyr 最後のバーストの 後に我々が仮定した星形成率の降下は、式 (1) で ω 一定と仮定したこと から生じるのだが、かなり現実的なように見える。SMC に適用した最終的なガス 比は Westerlund と一致する。LMC に関しては我々の値は彼が採用した < 8 % より少し大きいが、他の文献で使用されている値とは違わない。
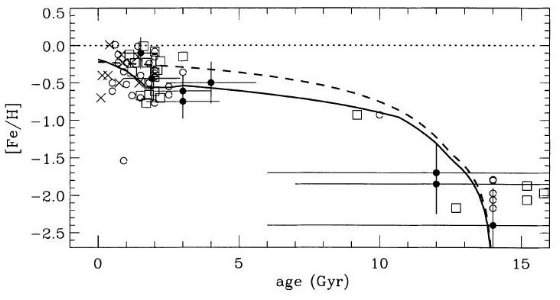
図3は LMC における O, Ne, S, Ar の年齢 - 存在量関係である。これらは 収率= 太陽近傍の 0.7 で、即時形成を仮定して得られた値である。バーストモデル の方がスムーズモデルよりフィットが良い。
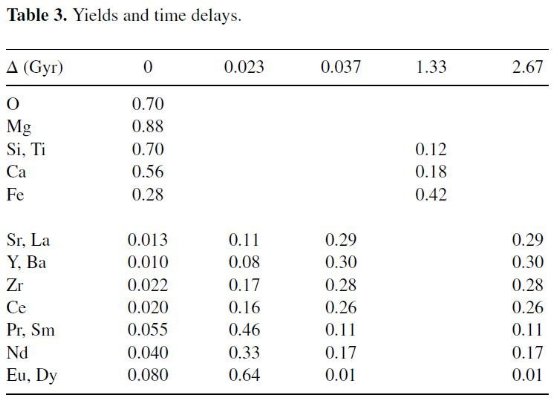
時間遅延
時間遅延を伴って放出される元素に対しては遅延形成近似(Pagel 1989) を使う。 これは星形成から決まった時間 Δt 経ってからその元素が放出され、一方 質量放出は星形成と同時であると仮定するものである。この場合、存在量 z2 の変化は次の式で表わされる。
| d | (gz2) = ω'g' - (1 + η)gz2g, t > Δ (12) | |
| du |
ここにプライムは変数が時間 t の代わりに時間 t - Δ で取られることを 意味する。式 (12) は少しの計算の後、
| d | [z2(eηu - 1)] = ω'e(1+η)u[e-u' - e-(1+η) u'] (13) | |
| dt |
解
スムーズモデルでは、式(13) の解は、
| z2(u) = | e(1+η)ωΔ | [ | eη(u-ωΔ) - 1 | - (u - ωΔ) | ] | , | |
| eηu | η |
u > ωΔ (14)
バーストモデルでは、t ≤ t1 では ω =ω1, t1 ≤ t ≤ t2 では ω = ω2, t2 ≤ t ≤ t3 = T では ω =ω3 である。T = 14 Gyr は系の年齢である。 ω2 は静謐期を表現して 小さい値である。ω1 は初期のバーストを表わす。すると、式(13)で、
ω' = u' = 0 ( t < Δ) (15)
ω' = ω1; u' = ω1(1 - Δ) (Δ≤t≤t1+Δ) (16)
ω' = ω2; u' = ω1t 1 + ω2(t - t1 - Δ) (t1+Δ≤t≤t2+Δ) (17)
ω' = ω3; u' = ω1t 1 + ω2(t2 - t1) + ω3(t - t2 - Δ) (t2+Δ≤t) (18)
同様に、
u = ω1t, (t < t1)
= ω1t1 + ω2(t - t1) (t1 < t < t2)
= ω1t1 + ω2(t1 - t2) + ω3(t -t2) (t2 < t) (19)
このように、各時間区分内、Δ から t1 (Δ>t1 なら t1 から Δ)、t1(又はΔ) から 、Δ + t1、Δ + t1 から t2、t2 から Δ + t2、Δ + t2 から t3 = T では、ω' = 一定である。そして、式(13) の指数は時間の線形関数である。
(1 + η)u = p + qt,
u' = r + st (20)
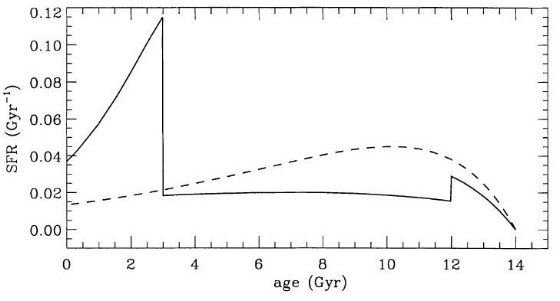
図1. LMC のモデル星形成史。
実線:表1によるバーストモデル。破線: u = 0.18 t のスムーズモデル
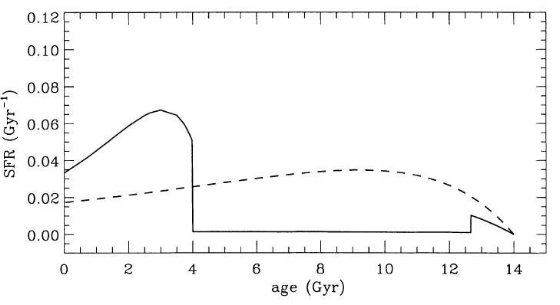
図2. SMC のモデル星形成史。
実線:表2によるバーストモデル。破線: u = 0.115 t のスムーズモデル
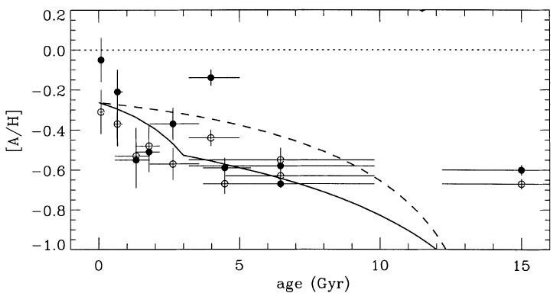
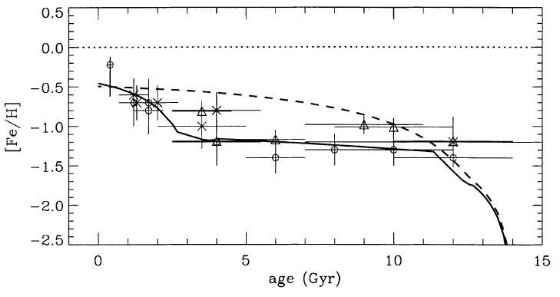
図3. LMC α元素の 年齢 - 存在量関係。線は図1と同じ。
白丸=酸素。黒丸=Ne,S,Ar の平均値。(dopita et al 1997)
したがって、式(13) は各時間区分 ta < t < tb ごと に解析的に解け、
z2(tb)(eηub - 1) - z2(ta)(eηua - 1)
| = ω' | ep-r | { | e(q-s)tb - e(q-s)ta | } | |
| q-s |
| - ω' | ep-(1+η)r | { | e[q-(1+η)s]tb - e[q-(1+η)s]ta | } | (21) | |
| q-(1+η)s |