| 星周シリケイトの吸収度の観測から (n, k) = 複素屈折率を導いた。 モデルでは、星周ダストの半径分布を n(a) ∝ a-3.5 と仮定 した。また、楕円率も連続分布するとした。Cabs(λ)/V = ダスト粒子の体積当たり吸収、はシリケイト鉱物の静誘電率の実験室データから 制限を付けた。 星周ダストは星間空間で風化される。その結果、バンド強度が強まり、18 μm と 10 μm の吸収比を星周ダストより大きくする。 | シリケイト内に様々な、酸化物、硫化物、炭化物、非結晶炭素、金属イオン などが混ざる効果は有効媒質理論で計算した。その内いくつかは, 2 - 8 μm で吸収係数 k を上げ得る。これは、実験室シリケイト吸収データを星間空間や 星周空間での観測値と合わせるのに必要である。他の効果は 18μm/10μm 強度比に関連する。 星周シリケイトと星間シリケイトの夫々に対して、 (n. k) の表を与えた。 2 - 8 μm 帯で要求される吸収率に関しては鉄と磁鉄鉱 Fe3O4 が与える。 |
| 星間グラファイトとシリケイトの光学定数は、実験室データと天体観測とを 合わせて、 Draine, Lee (1984) が決定し、 Draine 1985 で表にされた。この天体シリケイトが実際に何である かを、現実の物体で同定したい。最近 Bussoletti et al 1988 などでは実験室 データの集積が進んでいる。 | この論文ではシリケイトの光学定数を調べる。星周ダストの吸収観測から、われわれは サイズ分布を仮定して解析して光学定数を決めた。次に、実験室データを用いて、 "ダーティシリケイト"の光学定数を推定した。また、星間空間でそれがどう変化するかを 議論した。 |
|
定義と基本式 ε = m2 = 複素誘電率 m = n + i k = 複素屈折率 レーリー限界 a << λ/2π では、Cabs = 総吸収 断面積、V = 媒質体積、とすると、
ここに、εm = 媒質誘電率、ε = ε grain/εm = 媒質に相対的なグレイン誘電率、 λ = 真空中での波長、λm = λ/nm = 媒質中での波長である。 関数 f(λ) = (ε(λ) - 1)/(ε(λ) + 2) の虚数部が既知の時、クラマース・クロニッヒ関係式、またはクラウジウス・ モソッティの分散解析を用いて Re[f(λ)] を導ける。Dorschner et al 1988 のレビューを見よ。分散関係の方法はフィットから細かい構造が抜け落ちる ことである。 |
別法 Martin, Rouleau 1991 は ε だけでなく f(λ) にもクラマース ・クロニッヒ関係が適用できることを注意した。すると、
ここで、 P は積分の主値である。通常外挿はべき乗形を仮定する。Tielens, Allamandola 1987 はその指数がグレイン物質が非晶質か結晶かで変わると 述べている。積分に対する非常な高周波数側の寄与は ε ∞ に帰結する。Rouleau, Martin 1991 はこの方法を炭素 の実験室データの解析に用いた。 Cext(λ)/V が物理的に可能かどうかのチェックには クラマース・クロニッヒ関係が用いられる。Purcel 1969 によると、それは
|

|
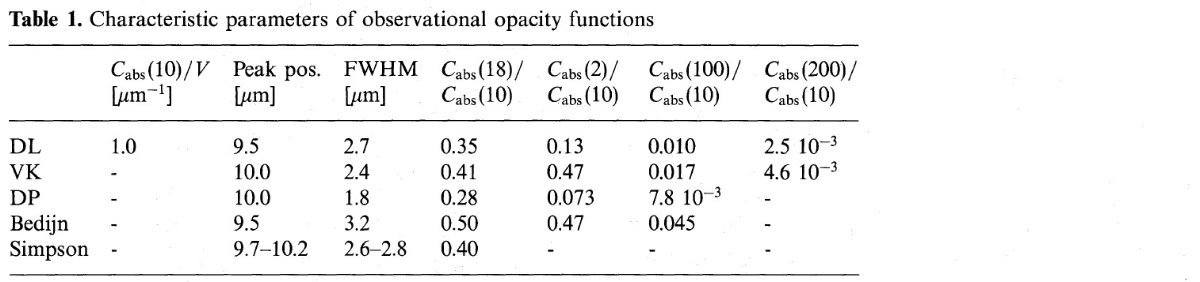
シリケイト放射 晩期型星星周ダストからの赤外放射はダストの光学的性質に強い拘束を掛ける。 しかし、放射は温度と密度の分布に影響される。IRAS LRS は 8 - 23 μm で 多彩な広がりを示した。この多様性の原因は Nuth, Hecht 1990 によって考察 された。我々は主にシリケイトの b = Cabs(18μm)/ Cabs(10μm) の振る舞いを調べる。 観測的吸収関数 図1は色々な研究で得られたシリケイトの吸収率を示す。表1にはシリケイト ダストの吸収ピークの特性を示す。 Bedijn 1987 は M-型ミラと OH/IR 星の NIR および IRAS 観測を、特に OH 26.5+0.6 の観測に基づいて、吸収率の パラメタ―表示を行った。Volk, Kwok 1988 は 467 AGB 星の IRAS データから 平均吸収率関数を導いた。David, Papoular 1990 は M-型超巨星データを解析 した。Simpson 1991 は光学的に薄いと思われる 117 晩期型星からの LRS スペクトルを用いた。電子遷移は考慮せずに UV 側に外挿してあるので図1 の UV 領域の値は信用できない。また、 Rowan-Robinson 1986 は 100 μm フラックス較正を間違えているので採用しない。 バンド強度比 b バンド強度比 b はダストモデルに依存する。 Draine, Lee (1984) と Simpson 1991 は b の値を仮定した。大多数の研究では b = [0.3, 0.5] の範囲にあるが、 Bedijn 1987 は OH/IR 星で b = 0.8 であるが、ミラ型星 では b = 0.5 と言う結果を得た。これは OH/IR 星の外層部でダスト温度が 低いためと]説明された。b の最も包括的な研究は Volk, Kwok 1988 が行い b の平均値 0.41, 10 μm ピーク 9.5 - 10.2 μm, その FWHM = 1.8 - 3.2 μm を得た。 ダーティシリケイト シリケイトの近赤外吸収率は星周シェルのエネルギー収支にとって非常に 重要である。地上シリケイトはこの波長域で k ≤ 0.001 と非常に透明で ある。しかし、 Jones, Merill (1976) と Bedijn 1977 は晩期 M-型星からの IR フラックスのシミュレイションが 唯一可能になるのはシリケイトグレインの近赤外吸収がかなり強い場合に 限られることを示した。また、Raveendran et al 1991 の偏光観測も類似の 証拠を提供した。 Jones, Merill (1976) は隕石の光学的性質 (Dorschner 1968) に類似した、"ダーティシリケイト" を提唱した。このシリケイトはニッケル鉄物質を含んでいる。様々な研究による ダーティシリケイトの k の評価は一桁に亘る違いを示す。2 μm で Rogers et al 1983 は k = 0.01 を示唆したが、 Jones, Merill (1976) の値は 0.1 であった。 Draine, Lee (1984) は中間を取って、 k = 0.03 を採用した。 |
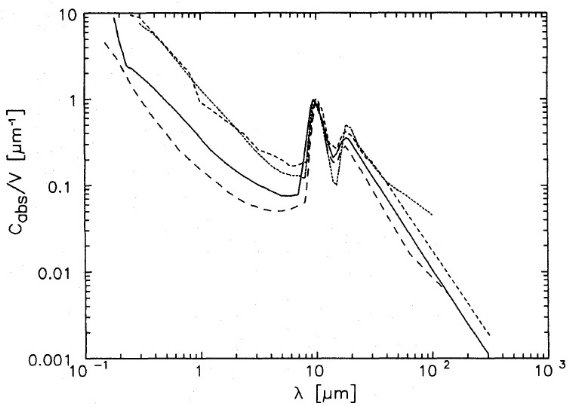 図1.星周シリケイトダストの吸収率。破線= Bedijn 1987。 端破線= Volk, Kwok 1988. 長破線=David, Papoular 1990. 実線= MRN サイズ分布に従う Draine, Lee (1984) シリケイト。 もう少し大きな k Collison, Fix 1991 は、 彼らの高空間分解星周マップを説明するには、 Draine, Lee (1984) の光学定数と a = 0.1 μm から導かれる Qabs/Qsca = 5 は低すぎると結論した。彼らは星周ダストの光学性質は Draine, Lee (1984) の与えたものと異なるのではないかと述べている。k をもう少し大きくすると 都合がよい。我々は第7章で k = 0.07 のモデルを調べる。 我々はそのように大きな k は、カラーセンターや宇宙線による損傷では不十分 で、他の物質がシリケイト中に混入する結果生じると考える。 遠赤外 第2章で [Cabs(λ)/V] は λ-1 より 速く落ちないといけないことを示した。[Cabs(λ)/V] ∝ λ-n を仮定した時、層状シリケイトでは n = 1 - 1.5, 3-次元シリケイトでは n = 2 (Tielens, Allamandola 1987) が期待される。 図1を見ると、 Draine, Lee (1984) と Volk, Kwok 1988 は n = 2, 他の二つはそれより緩い。Sopka et al 1988 彼ら独自の観測から、 は Cabs(200)/Cabs(10) = 0.01 - 0.02 とした。 この値の新しい観測が ISO で期待される。 |
|
粒径と形 粒径と形の分布を以下のように仮定する。 n(a) ∝ a-3.5 (a = [0.01, 0.25] μm) P(L1, L2) = 120 L1L2 (1-L1-L2) L1 と L2 は Bohren,Huffman 1983 の楕円率で球に対して L = 1/3 である。 クラマース・クロニッヒ法を採用 クラマース・クロニッヒ関係、またはローレンツプロファイルフィットは データと非常に良く合う。しかし、クラウジウス・モソッティ法では細かい構造 の再現はできない。ただそれは必ずしも欠点ではなく、例えば図1の David-Papoular 1990 曲線に現れる 8, 60 μm の非物理的な勾配不連続は クラマースクロニッヒ法でも繰り返されるが、クラウジウス・モソッティ法で は平滑化消去される。この先では、その直接性のために、クラマースクロニッ ヒ法を採用する。 ε∞ 光学定数導出に際しては二つのパラメタ―を与える必要がある。一つは ε∞ = 電子遷移の誘電率への寄与。我々は実験室の シリケイトデータを採用する。Dorschner 1968 によると、シリケイトグラス に対する値は狭い範囲に収まり、オリビンで 2.7, パイロキシンで 3.4 である。 そこで、 Draine, Lee (1984) と同じ平均値の ε∞ = 2.94 とする。 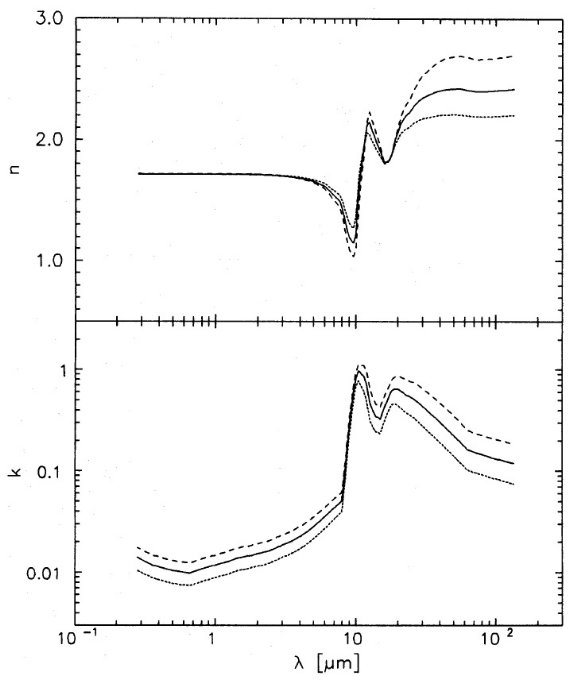 図2.David, Papoular 1990 の光学定数 (n, k). 点線は Cabs(10)/V = 0.68 μ-1, 実線は Cabs(10)/V = 0.90 μ-1, 破線は Cabs(10)/V = 1.13 μ-1 を仮定。 |
Cabs(10)/V もう一つのパラメタ―は吸収強度の絶対値である。観測からは Cabs(λ)/V しか分からないので、 Cabs(10)/V を仮定する必要がある。実験室データとしては、 小さい方では非晶質オリビンスモーク (Stephens et al 1988) の 0.2 μm-1 から、大きい値としては結晶性黒曜石(変だな?) の 2.3 μm-1 に亘る。ただし、両極端値の幾つかが測定エラー による可能性はある。一般には結晶質シリケイトの方が非晶質物質よりも吸収 が強い。 ε0 の制約 クラマース・クロニッヒ関係によると、全ての共鳴の強度の和は静誘電率 ε0 に関係するので、逆にそれから、Cabs(10)/V を求めることが可能である。λ0 は遠赤外として、もしも、 λ < λ0 で ε∞ と Cabs(10)/V が分かっていて、λ > λ0 にはもう共鳴がないならば、ε0 は Cabs(10)/V と直接結びつく。もし、λ > λ0 にいくつかの 共鳴があるなら、Cabs(10)/V の上限が得られる。吸収の絶対値と ε∞ の関係を示すため、図2では David, Papoular 1990 の相対吸収データに、規格化定数 Cabs(10)/V = 0.68, 0.90, 1.13 μm-1 の3通りに対してクラマース・クロニッヒ計算 を行った結果を示す。様々なガラス状物質に対する ε0 は、純粋のコルツガラスで 3.8, 鉛ガラスで 16 (Landolt-Borenstein 1957) である。Mg シリケイトでは 5.5 - 6.5, Fe シリケイトで 6.8 - 7.5 (Touloukian, Ho 1981)である。我々は平均値 6.5, つまり 静屈折率 ε01/2 = 2.55 を用いる。David, Papoular 1990 データに対しては、この ε0 から導かれる Cabs(10)/V = 0.57 μm-1 である。 光学定数の比較 図3では、色々な研究による相対吸収率から得られる光学定数を比べた。 Bedijn 1987 に対してはその内の一つ b = 0.5, Cabs(100)/ Cabs(10) = 0.045 モデルを使用した。図3を見ると、近赤外 での吸収率の違いは k = 0.015 - 0.07 として現れる。観測吸収率から 導かれる光学定数は比較的似ている。 n に関して、 Draine, Lee (1984) からの定数のみは長波長側で他と異なる。k については、 10 - 30 μm での 違いが生じるのはバンドの振る舞いの差が原因であることは明らかである。 より長波長側で λ-1 (Bedijn 1987) や λ-1.4 (David, Papoular 1990) のように反り返ると、 k の勾配に非物理的な不連続をもたらす。Bedijn の定数は長波長側では 非現実的に見える。 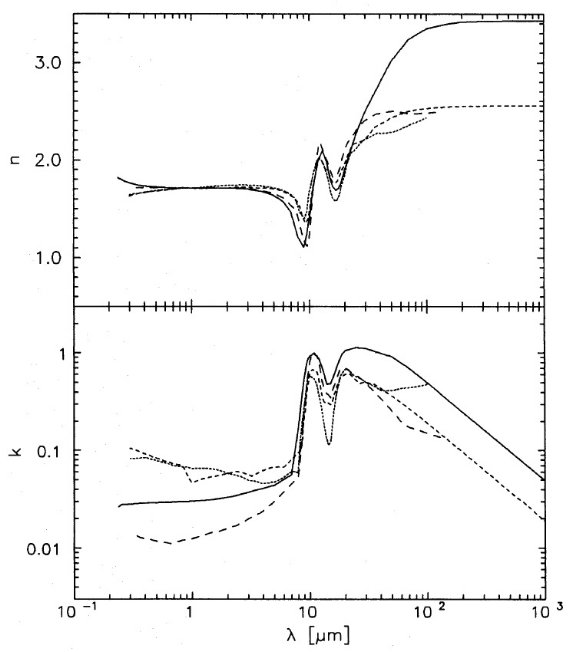 図3.光学定数の研究間比較。点線=Bedijn 1987. 短破線=Volk, Kwok 1988. 長破線=David, Papouar 1990. 実線=Draine 1985 の天体シリケイト。 |
|
シリケイト 10 μ/18 μm 強度比 希薄星間空間でのダストの減光及び放射には多種類のダストが関係するので、 そこからシリケイトダストの吸収率を抽出することは簡単でない。例えば、 IRAS 12, 25 μm 放射はかなり高いが、炭素、炭素・シリケイト非一様、 グレイン表面の黒いマントル、ダーティシリケイトのどれもがそれに寄与 できる。しかし、それでもシリケイトダストへの制約は導ける。 10 μm 星間吸収帯の形は星周 10 μm 放射と似ている。しかし、星間吸収 では b = 0.6 (Roche 1988) であるが、星周放射では b = 0.41 で異なる。 従って、星間空間においてダストの変成が起きたのであろう。勿論、他物質の 混入による b の変化も考えられる。 10 μm 帯強度の観測 希薄星間空間における Cabs(10)/V を決定するには、シリケイト 帯を固有スペクトルに含まない天体を使って、τ(10) を測る必要がある。 Becklin et al.1978 は銀河中心に対して Av/τ(10) = 8、Cohen et al 1989 はかなりの不定性を含み、 WC 星に対して Av/τ(10) = 40 を得た。同じ星 について Roche, Aitken 1984 は 18 を得ている。WC 星風からの強い 7.7 μ m 未同定バンドが解析を困難にしている。Whittet 1984 の元素消失率から推定 すると、可視全減光に対するシリケイトの寄与は 60 - 80 % に上る。 |
太陽近傍
と銀河中心方向とで Av/τ(10) が異なる理由は、銀河面内の O/H 比勾配
(Wink et al 1983, Shaver et al 1983) に伴う Si/C 比の違いにより、Av に
対するシリケイトの寄与が銀河系中心方向で大きくなるのかも知れない。
MNR 分布は可視減光を一定にする MNR サイズ分布に従うグレインの可視減光はシリケイト程度の屈折率において は k の大きさにあまり依存しないことが判った。k を大きくしても、可視減光 は Cabs(0.55)/V = 6.4 μm-1 に留まり、増大しない のである。その結果、 Av/τ(10) は Cabs(10)/V に対する制約 となる。メタル量効果を考慮すると、Cabs/V のピーク値は 0.3 - 1.0 μm-1 となる。Aitken 1989 の偏光観測はバンド強度 0.75 - 1.4 μm-1 を示す。 遠赤外減光 希薄星間空間の FIR 減光は非常に不確かである。Hildebrand 1983, Renegarajan 1984, Pajot et al 1989, Casey 1991 の減光を共通の 200 μm で評価すると、 Cabs(200)/V = 0.004 - 0.02 μm-1 となる。我々の 最終モデルではシリケイトの減光はその下限値付近になる。おそらく、他成分の 寄与がかなり効いているのであろう。 |
|
冷却速度の効果 Nuth, Hecht 1990 は実験室データに基づいて、急速に冷える星風中ではシリ ケイト中の酸素が大きく欠乏するが、一方星間空間や低速の星風中のシリケイ トは Si/O が化学当量比になるとした。この考えは Stencel et al 1990 が ミラ型星の IRAS LRS のシリケイト輻射を並べたものと一致する。酸素欠乏型 のシリケイトはピーク吸収が弱く、b が小さく、近赤外吸収が弱い。酸素が 多い環境では Fe は磁鉄鉱=マグネタイト (Fe3O4) や 赤鉄鉱=ヘマタイト (Fe2O3) が形成される。 |
温度効果と種ダスト Day 1976 は低温 ISM でバンド強度と b が大きいのは温度効果であるとした。 希薄星間空間と晩期型星大気でのダストマントルの形成は未解決の問題である。 様々な凝集計算によると、シリケイトは他の鉱物の種粒の上に沈殿する可能性 がある。種としては MgO (Fadeyev 1988), MgS (Kohler 1991), Al2 O3 (Onaka et al 1989), Fe, Fe2O3, Fe3O4 (Laureijs 1989, Nuth, Hecht 1990) が提案 されている。 |
|
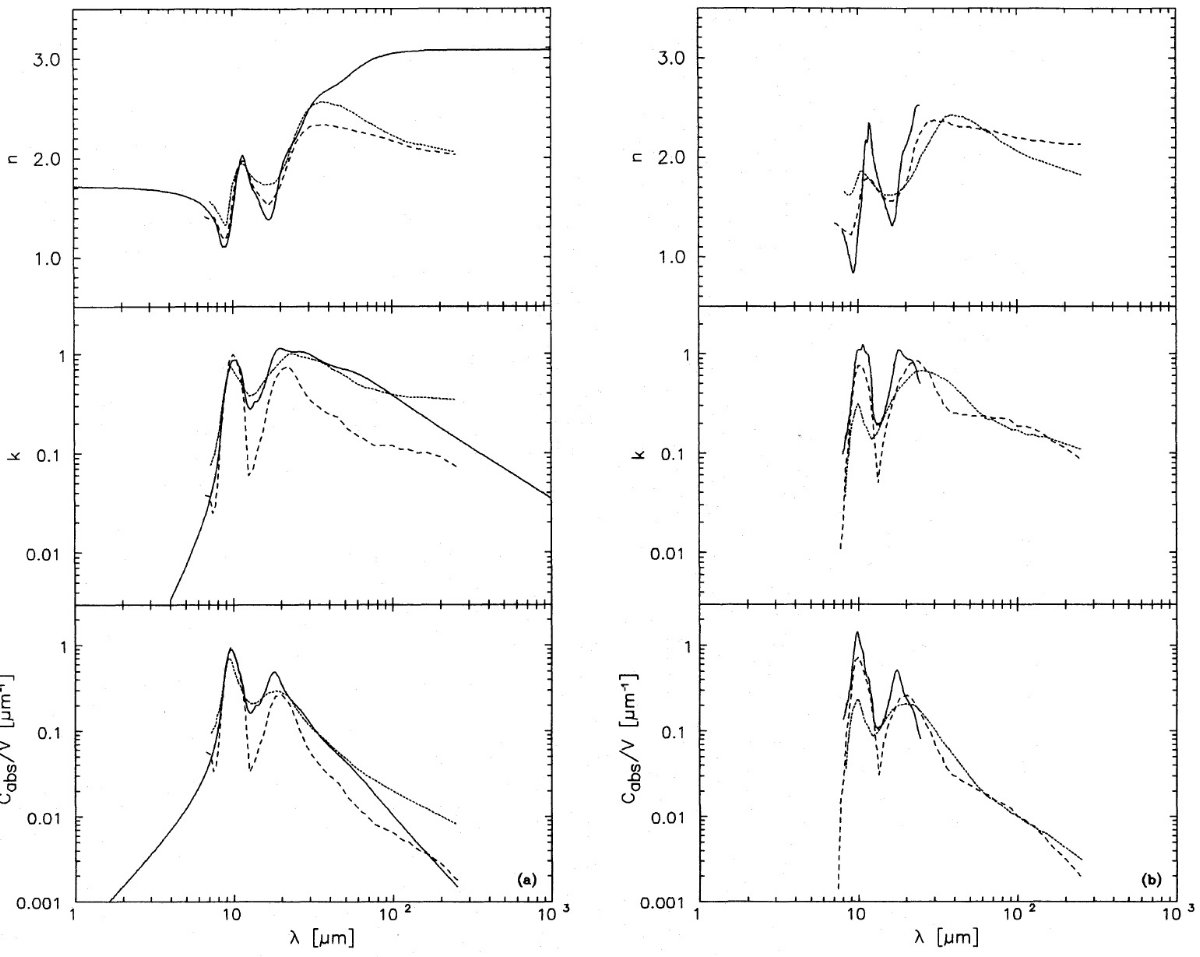
酸素欠乏シリケイト 地上シリケイトの光学的性質に関しては多くの実験, Dorschner, Henning 1986, がある。それらの多くは結晶質である。酸素欠乏シリケイトの光学 的性質の幾つか Wada et al 1991 からは未だに光学定数を直接に導くことが できない。しかし、それでも Nuth, Hecht 1990 の酸素欠乏シリケイトは バンド比 b が小さいという結論を確認する。 実験室で作った非晶質シリケイトの光学定数 図4には実験室で作った非晶質シリケイトの光学定数と相対吸収 Cabs(λ)/V をレイリー限界の仮定で示す。図4左(a) は パイロキシン (Mg,Fe)SiO3 組成、右(b) はオリビン (Mg,Fe)2SiO4 組成である。データは、 Day 1979, 1981, Kartschmer, Huffman 1979, Dorschner et al 1988 から採った。Dorschner et al. 1988 のオリジナルデータの代わりに我々は、 ブロンザイト(Mg0.9Fe0.1)SiO3 をポリエ チレンに封じて、集合効果を補正して実験を行った。それらは長波長側でより 正確になったはずである。しかし、光学定数の測定は困難であり、公表された 値はエラーを含んでいるに違いない。例えば、ブロンザイトの長波長屈折率は 高過ぎるように見える。フラクタル効果 (Ossenkopf 1991) やサイズ効果が その高い原因ではないことを示した。 |
10 μm 吸収のピーク位置と形 図4左(a) から、10 μm 吸収のピーク位置と形は種々のパイロキシン間 でよく似ているが、λ > 20 μm では光学定数の絶対値が異なる ことがわかる。ブロンザイトの強い 18 μm 吸収からのクラマース・クロニ ッヒ積分への寄与は長波長領域で、他のシリケイトよりも大きな屈折率となっ た。図4右(b) ではオリビンが 10 μm 帯は似ているが 20 μm 領域で 互いに相違することを示す。 Day 1979, 1981 曲線は、 FeSiO3 を 除き、20 μm 付近の屈曲振動のピーク波長が他の実験物質や観測値より長い。 一般に、パイロキシンの 10 μm 帯はオリビンより短波長側にある。 Mg シリケイト吸収帯は幅広で観測に合う 表2には様々な実験室非晶質シリケイトの吸収率の特徴を示す。 Fe2SiO4 サンプルと照射オリビンは他の実験室サンプル や観測から得られたパラメタ―と合わない。表1を見よ。観測からはかなり 幅広の 10 μm 帯が要求される。この性質はブロンザイトサンプル、 MgSiO3, Mg2SiO4で最もよく 満たされる。これらのシリケイトは Cabs(10)/V = 0.75 - 1.0 μm-1, b = 0.3 - 0.5, Cabs(100)/Cabs(10) = 0.01 - 0.03 を示す。 |
|
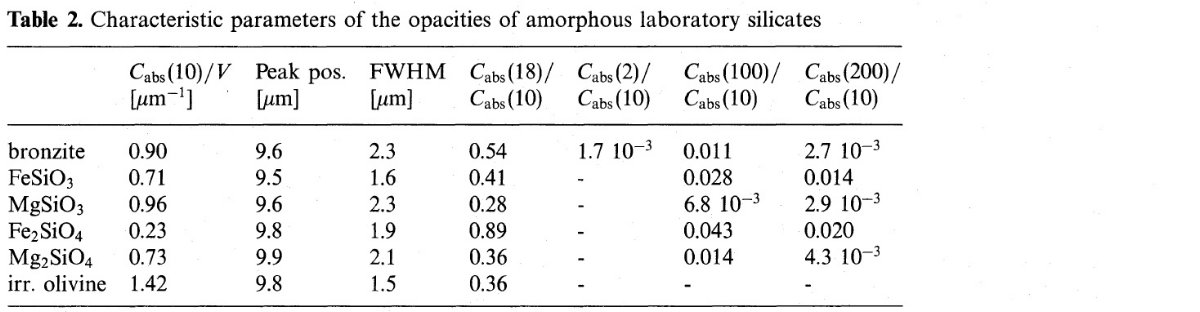
計算法 含有物の体積比率が 5 % 以下の場合はマクスウェル・ガーネット則を、 5 - 20 % の場合にはブラゲマン (Bruggeman) 則を適用 (Ossenkopf 1991) する。有効媒質理論(effective-medium theory)を短波長側にも適用する ため、含有物は波長に比べて十分小さいが、巨視的光学定数を適用できる ほどには大きいと仮定した。そのような非一様物質グレインにレイリー 近似を応用した。使用した光学定数の出典は表3に示す。 図5=ブロンザイトに色々な粒子 図5にはブロンザイトに Al2O3, MgO, MgS 含有物を 入れた効果を示す。10 % 例は Onaka et al 1989 から採った。含有物が近赤外 と遠赤外で効果を示さないことが判る。 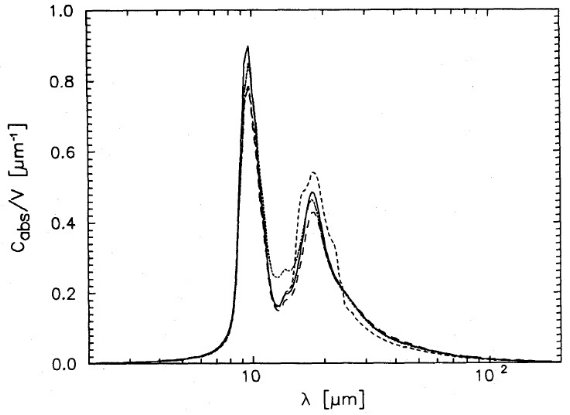 図5.レイリーグレインの吸収率。実線=ブロンザイト。点線=アルミナ含有物 を 10 % 含むブロンザイト。短破線= MgO 含有物を 10 % 含むブロンザ イト。長破線= MgS を 10 % 含むブロンザイト。 |
Al2O3 は 10
μm 吸収バンドを 9.7 μm に移し、巾を 2.7 μm に広げた。MgO はバン
ド比 b を 0.68 に上げた。MgS は変化を生じなかった。
図6=鉄系含有物 図6では鉄系含有物の効果を比べた。体積比率は鉄原子の数が同じになる ように選んだ。 図6は近赤外における劇的な吸収率の増加を示す一方、吸収帯には殆ど影響が ないことが特徴である。マグネタイト含有物は最も近赤外吸収増加が大きい。 Cabs(2)/Cabs(10) = 0.04 (Fe), = 0.08 (Fe2 O3), = 0.22 (Fe3O4) である。対応する k(2) = 0.009(Fe), = 0.014 (Fe2O3), = 0.05 (Fe3O4) である。FIR では吸収増加は起こらない。 Fe2O3 のみが b = 0.64 と増大効果を示す。n は全て の場合で,2 μm で 0.08, 200 μm で 0.20 の系統的増加を示した。 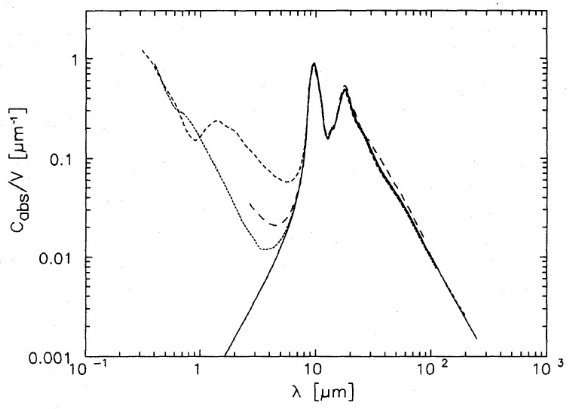 図6.レイリーグレインの吸収率。実線=ブロンザイト。点線=固体鉄含有物 を 3 % 含むブロンザイト。短破線=マグネタイト含有物を 6 % 含むブロンザ イト。長破線=ヘマタイト(赤鉄鉱)を 6 % 含むブロンザイト。 |
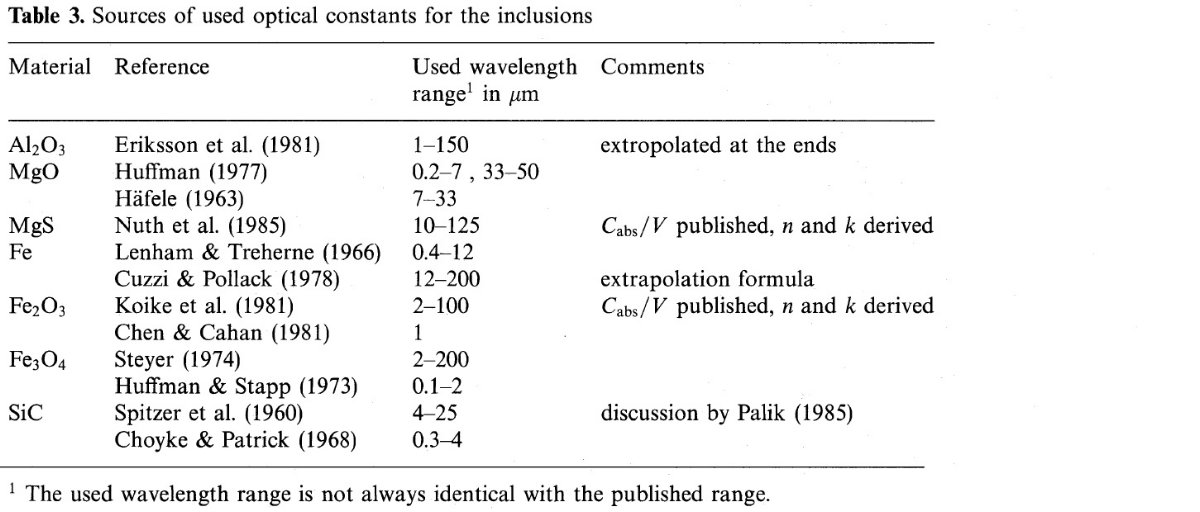
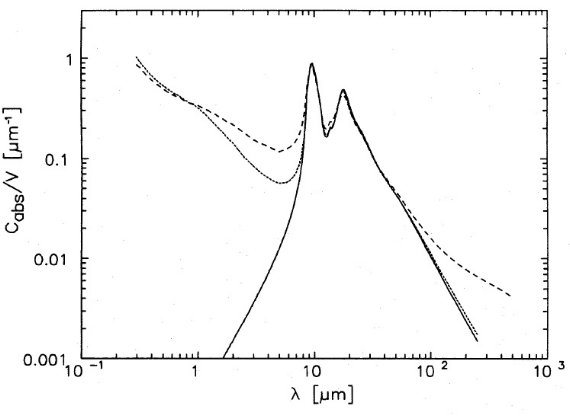 図7.レイリーグレインの吸収率。実線=ブロンザイト。点線=非晶質炭素含有物 を 5 % 含むブロンザイト。破線=同体積の非晶質炭素マントルで覆われたブロンザ イト。 図7=非晶質炭素含有物 図7は、ブロンザイトへの非晶質炭素の含有物の効果、マントルになった時 の効果を示す。非晶質炭素の光学定数は Edoh 1983 から採った。炭素は近赤外 において、鉄系含有物と同様の吸収増加を引き起こす。 Cabs(2)/Cabs(10) = 0.17 (炭素含有物)、 = 0.27 (炭素マントル)である。遠赤外ではマントルは含有物よりも効果が大きく、 Cabs(200)/Cabs(10) = 0.003 (炭素含有物)、 = 0.10 (炭素マントル)である。ただし、非晶質炭素の光学定数は不確かで、 Rouleau, Martin 1991 の値では含有物とマントルの効果の差は小さい。 図8=SiC SiC バンドは 含有物比が 10 % を越えないと、シリケイト帯に隠されている ことが図8から分かる。SiC は 11.2 μm 帯で Re[ε(λ)] が 強い負値となる。これはグラファイトが 0.22 μm でそうなるのと同じである。 このような粒子では表面モードの強い共鳴が起きるが、その位置や形は粒子の 形に影響される。しかし、図9に見るように、計算の結果では含有体に関して は形状効果は小さい。 |
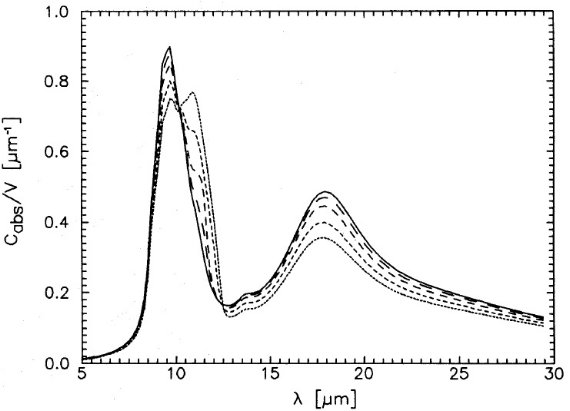 図8.レイリーグレインの吸収率。実線=ブロンザイト。点線=シリコンカー バイド含有物を 2 % 含むブロンザイト。短破線=シリコンカーバイド含有物 を 5 % 含むブロンザイト。長破線=シリコンカーバイド含有物を 10 % 含む ブロンザイト。うんと長い破線= 15 %. 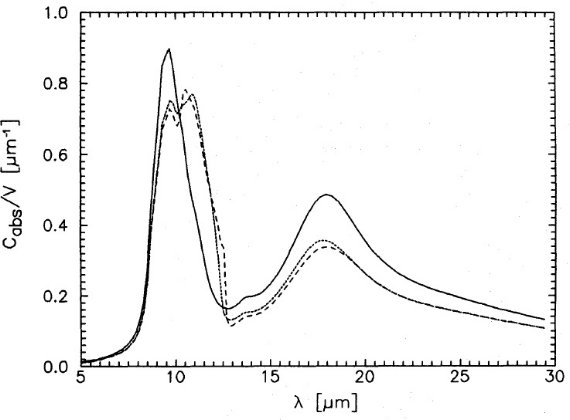 図9.レイリーグレインの吸収率。実線=ブロンザイト。点線=球形のシリコ ンカーバイド含有物を 15 % 含むブロンザイト。破線= CDE のシリコンカー バイド含有物を 15 % 含むブロンザイト。 |
|
星周シリケイト(1) やや酸素欠乏で非化学当量性のシリケイトが暖かい星周ダスト候補として Nuth, Hecht 1990 により提案された。その吸収率の代表として Volk, Kwok 1988 を選んだ。彼らが非常に注意深くデータ処理を行っており、データが 幅広い星から選ばれているからである。近赤外データが不足しているので、 観測的に導かれた吸収率は 2 - 7.5 μm が欠落している。したがって、 その部分を鉄と鉄酸化物の含有体を含む実験室シリケイトから計算した。 この波長帯での有効光学定数はシリケイトのタイプにあまり依らず、非常に 小さい k とほぼ一定の n で特徴づけられる。含有体の体積比は Cabs(2)/V が Volk, Kwok 1988 と同じになるように選んだ。 こうして、二つの吸収率は 7 - 8 μm で滑らかに接続された。バンド 比 b = 0.41 はシリケイト、従って鉄が部分的にしか酸化されていないこと を示す。それで、金属鉄と磁鉄鉱の鉄原子の割合を等量にした。もし、 ダストシェルの冷却速度が Volk, kwok サンプルよりさらに短い、または ダスト温度がより高ければ、b はさらに小さくなり、 鉄は金属鉄として 現れるだろう。 星周シリケイト(2) 我々の鉄、磁鉄鉱含有体を含むシリケイトの静誘電率は 3.2.節で述べ た純粋シリケイトの値とは異なるであろう。ε0 を変える と Cabs(10)/V の規格化を変えることとなる。従って付録に述べた 逐次近似により、[Cabs(2)/Cabs(10)], Cabs(10)/V, ε0 が整合するように調整する 必要がある。その結果は、 Fe3O4 6.3 %, Fe 3.1 %, Cabs(10)/V = 0.64 μm-1, ε0 = ε0(pure silicate) となった。吸収率は κ(10) = Cabs(10)/ρV = 2.0 103 cm2 g-1 である。 星周シリケイト(3) これら非一様グレインにクラマース・クロニッヒ関係が適用可能であろうか? Bruggeman miving は クラマース・クロニッヒ不変性を保存しない。しかし、 テスト計算の結果、Bruggeman miving によるクラマース・クロニッヒ関係 からの逸脱は小さいことが判った。結果は表10に示す。 星間空間シリケイト 冷たい酸素過多シリケイト吸収率の直接観測はない。我々は、Volk, Kwok 1988 の吸収係数を、Nuth, Hecht 1990 に従い、酸化が進んだら予期される方向に 人為的に二つの変更を加える。一つはシリケイトの酸素量を化学当量となるように 増やすことである。これは、ピーク吸収強度を増加させ、バンド強度比 b を増大 させる。含有体の酸素への影響も考慮した。その結果、ピーク強度は Cabs(10)/V = 0.75 μm-1, κ(10) = 2.5 10 3 cm2g-1 へと増大する。バンド比は b = 0.6 となる。長波長側で Volk, Kwok 1988 曲線になるように滑らかな遷移を 25 - 35 μm に施した。こうして決めた光学定数を図10に示す。 Si はシリケイト内 星風で星間空間に吹き飛ばされたダストはその後化学・物理的に強い変成 を受ける。もし、ダストの半分が炭素星起源とすると、 Si, Fe, その他の 元素の半分は当初カーバイドの中に存在するか、少なくともシリケイトとは 共存していない。しかし、ほぼ全ての Si がシリケイト中にないと H-原子 当たりのシリケイト帯強度を説明できない。この点は Tielens, Allamandola 1987 が強調した。 |
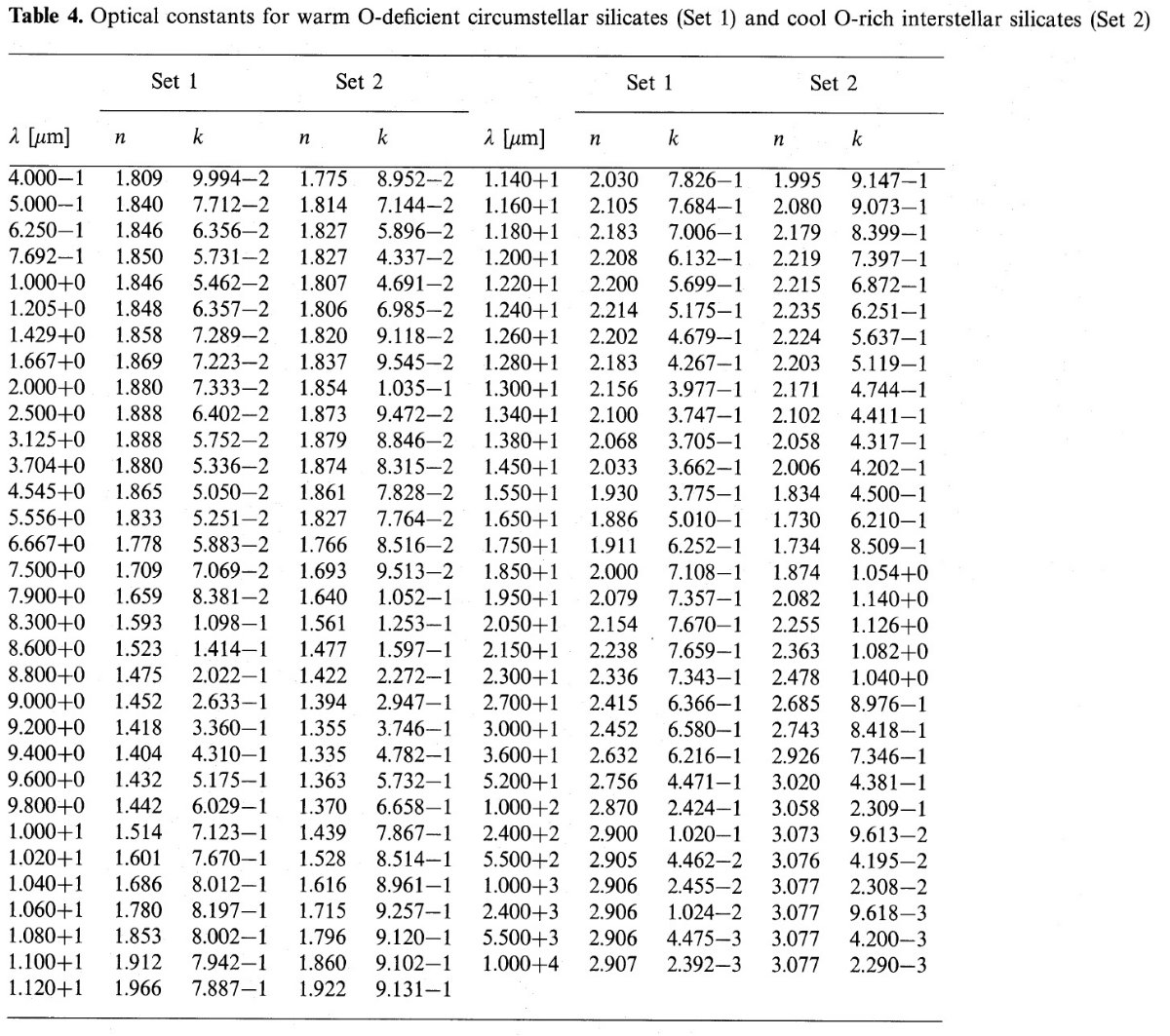
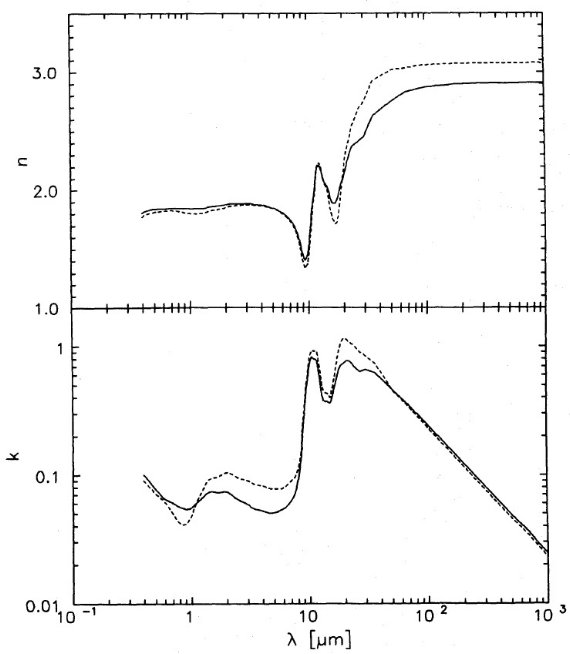 図10.実線=暖かい酸素欠乏星周シリケイトの光学定数。 破線=冷たい酸素過多星間シリケイトの光学定数。OH/IR 星も含む。 シリケイト内 Si 原子の量 我々の光学定数で、Av/τ(9.7) = 40 を説明するのに必要な Si/H を計算 した。観測的には E(B-V)/N(H) = 1.7 10-22 mag cm2 H-1 (Bohlin et al 1978), Av/E(B-V) = 3.1, それに、我々の (吸収 断面積/Si 原子) = [Cabs/V]μ/ρ である。 ここに μ = シリケイト分子の平均質量で大体 110 - 120 質量単位である。こうして、
を得る。これは Si の全存在比である。こうして、 9.7 μm 吸収を説明す るには、Si, Fe, その他の元素を炭素星起源の分も含め全て酸化して、 シリケイトに投入する必要がある。この酸化が星間空間に金属鉄が存在しない 理由であろう。 |
|
含有体 赤外観測から、天体シリケイトとして実験データに基づいた意味のある光学 定数を導くことが出来る。実験室データに基づいて、計算した非一様な構造の グレインの光学的性質から、光学定数を決めた。こうして以下の結論を導いた。 1.ダーティシリケイトは含有体が原因 星周ダストの吸収率観測は相対吸収率 Cabs(λ)/ Cabs(10) を与える。近赤外において、星間ダストの放射率は M 型星の星周ダストのそれと同じか、それ以上である。シリケイトの近赤外 におけるこの汚れは、鉄に関連する含有体で説明可能である。 |
2.星間空間での変成 吹き飛ばされた星周シリケイトは星間空間で変成作用を受ける。星周シリケ イトと星間シリケイトの光学的性質は比較的似ている。星間ダストに対する バンド強度比 b = 0.6 は星周ダストにおける値 b = 0.40 - 0.45 より高い。 3.SiCの量 我々は星間ダスト中のシリコンカーバイドの上限を 10 % に定めた。 |