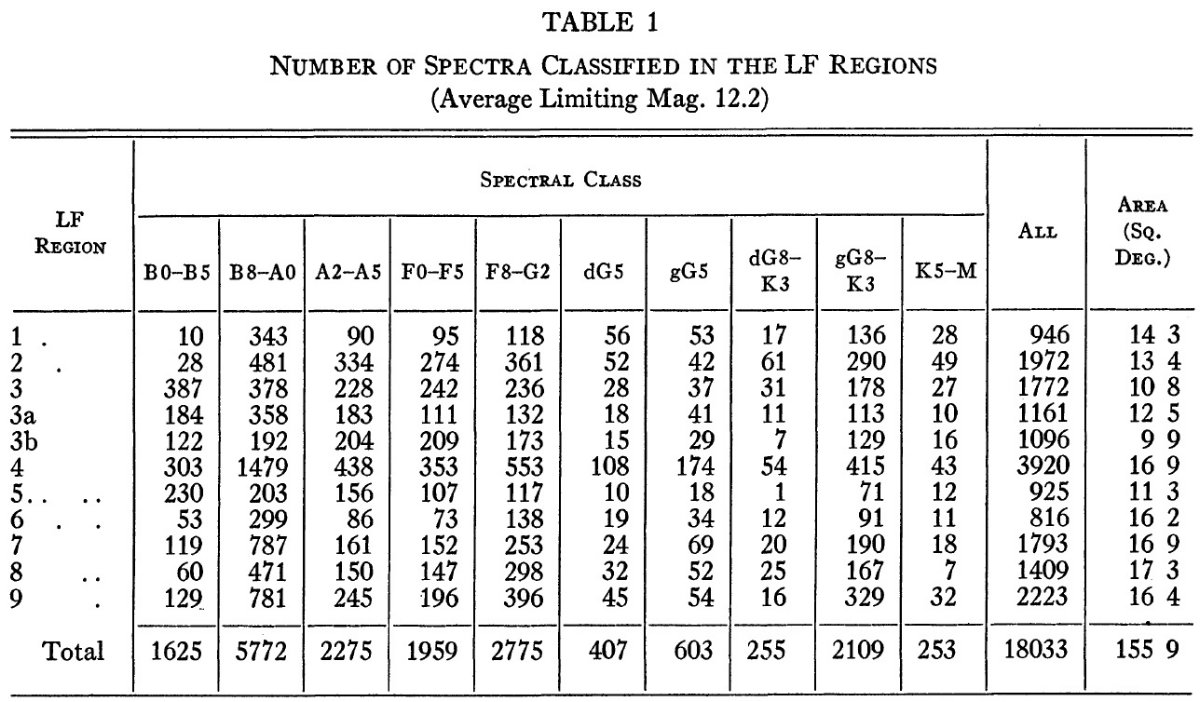
| 銀河系選択領域でのスペクトル型と写真等級を集めた 過去 10 年間の観測データをまとめた。太陽から 1 kpc 以内の銀河系構造 を表と図で表した。 | B8 - A0 と B5 星については 2.5 kpc まで構造を調べた。星間物質の分布は 2.5 kpc まで調べた。光度関数の揺らぎは log φ(M) で 0.6 まで 上がる。銀経と距離に対する揺らぎの平均は van Rhijn と一致する。 |

|
11 領域の観測 1945 年 ワーナースワゼイ天文台は銀河系 11 領域を選択して、銀河系の 構造と一般光度関数の場所による変化の研究を開始した。これまでの8論文 で、18,000 星の写真等級とスペクトル型が調べられた。本論文ではこれまでの 結果をまとめる。 選択領域 シグナス領域は B 型星が多く星間吸収もマダラであるが、その他の領域は 星の分布が不規則なところを避けている。それらの中心方向は計画の 最初 McCuskey, Seyfert 1947 に述べられている。 スペクトル型分布 表1には観測された星の数を示す。図1には領域毎の スペクトル型分布を図示した。 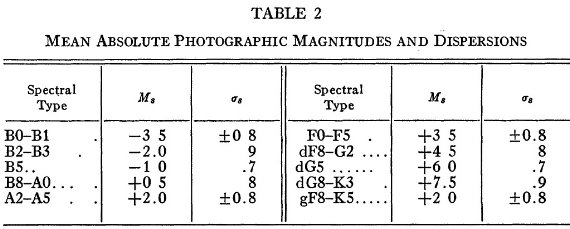 表2.平均絶対等級 |
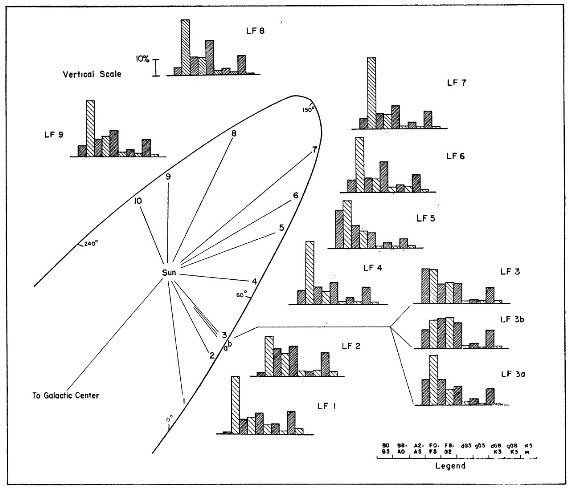 図1 LF 領域におけるスペクトル型の分布。写真等級の平均 限界等級は 12.2 である。. |
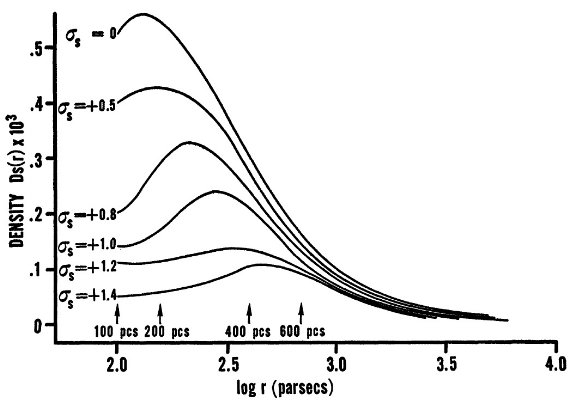 図2.LF4 領域、B8 - A0 星の密度関数 D(r)。仮定した σ による変化 に注意。 分散が密度分布に及ぼす影響 表2にはスペクトル型に対する絶対等級とその分散を示した。図2には LF4 領域、B8 - A0 星の密度関数 D(r)。仮定した σ を 0.0 から 1.4 まで変えた時の変化に注意。 σ が変わると、密度極大の 距離が大きく動く。実際の σ は 0.2 より大きくはないだろう。 |
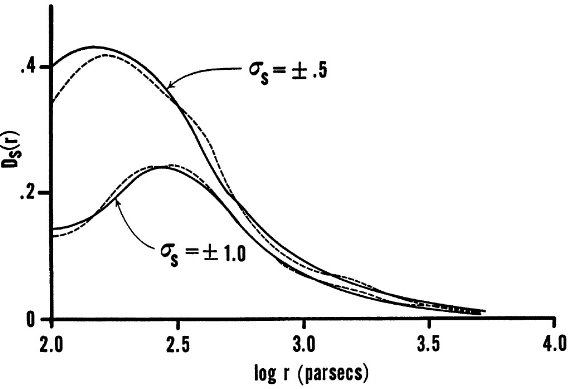 図3.二つの計算機によって計算された密度関数。縦軸は 103 pc3 当たりの星数。絶対等級に二種類の σ を使った結果 が描かれている。 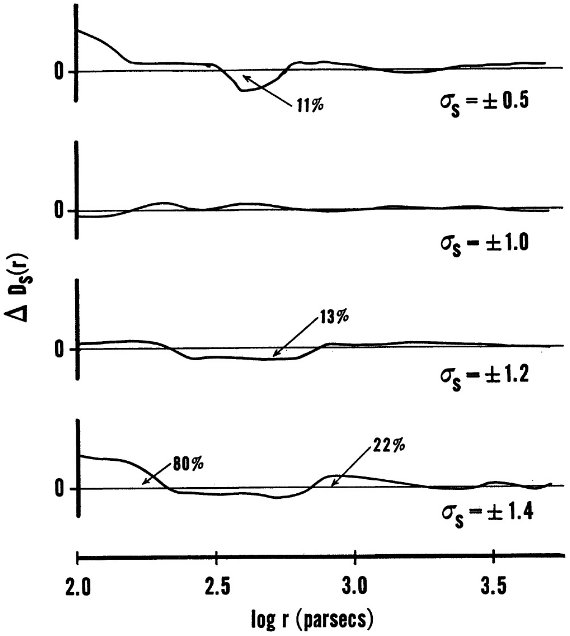 図4.二つの計算機による結果の差。 |
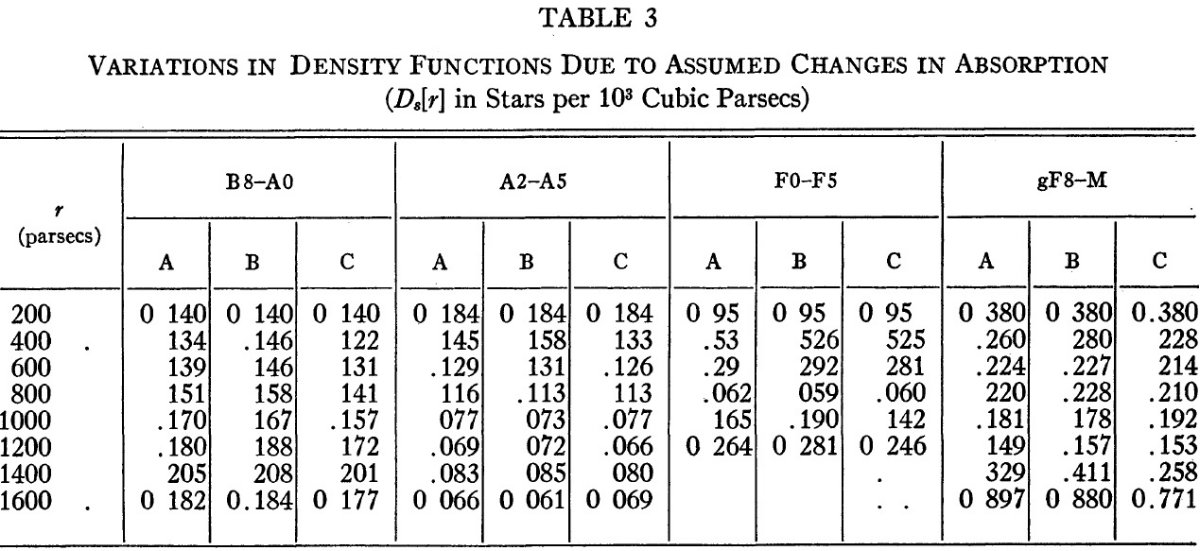
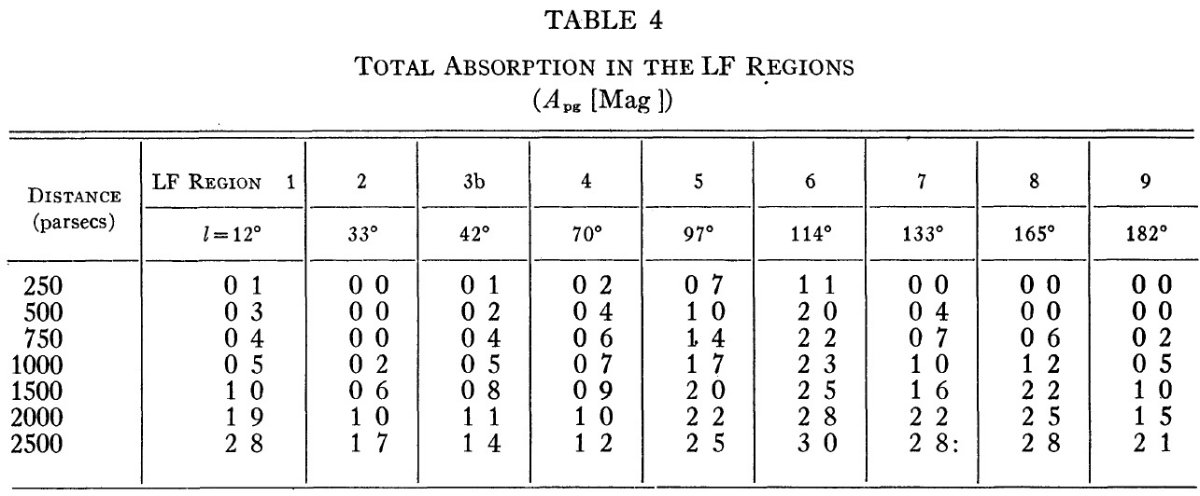
星間吸収の計算には A5 から早期の星の観測カラーを使う。各 LF 領域で
求めた結果は表4に載せた。 Apg/E = 2.6 とした。
図5はその結果を図示したものである。LF 6 領域を除くと、異常な
構造は示さない。
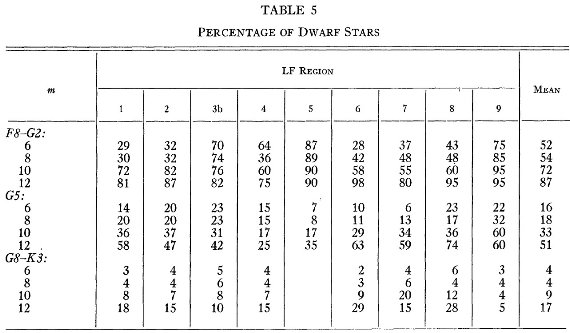 表5.矮星の割合。 |
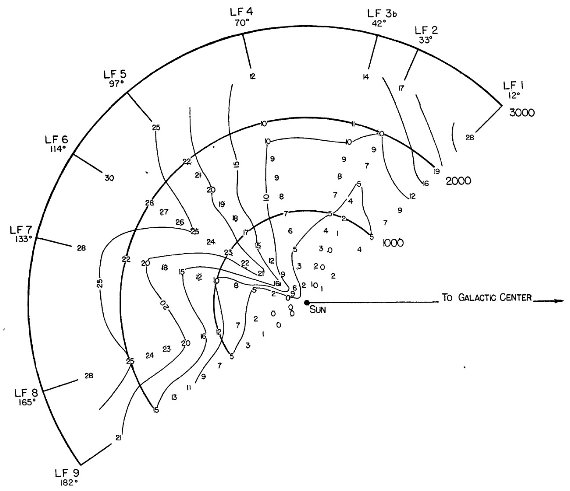 図5.LF 領域の星間吸収の分布。数字は (1/10)等単位の Apg |
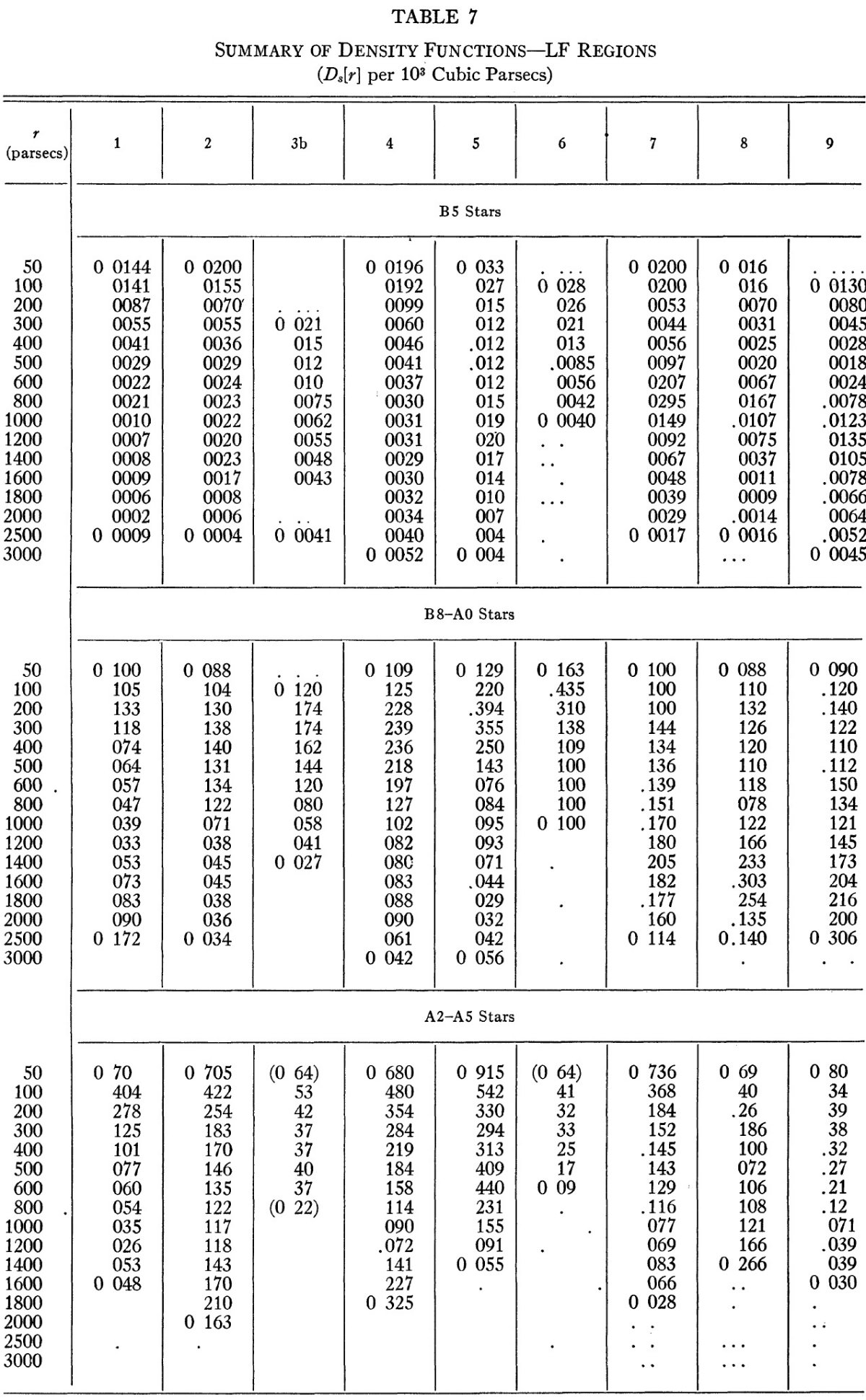
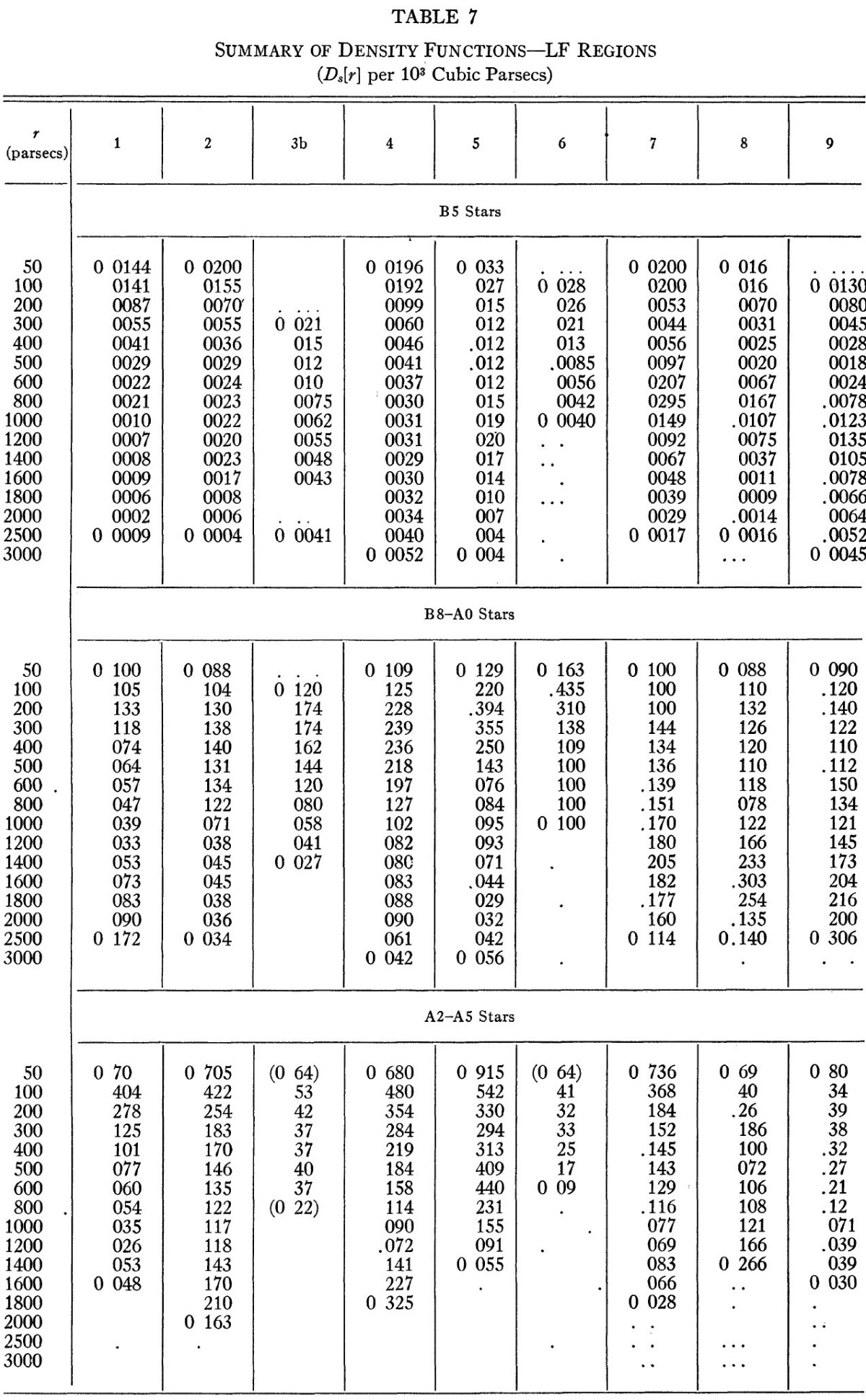
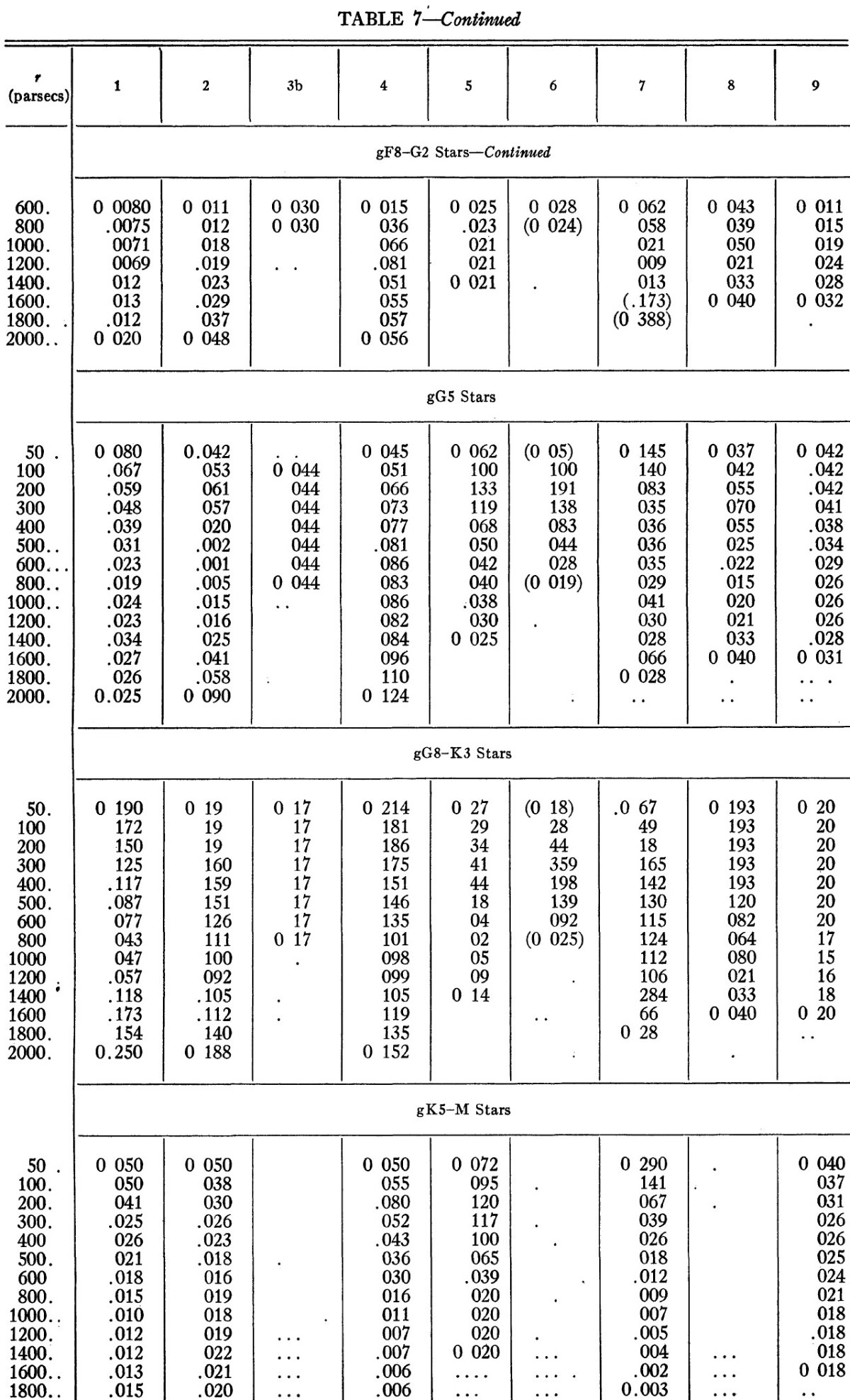
| 表7には、(m, logπ) 解析と星間吸収補正の結果得られた密度関数が 示されている。B5 より早期の星は解析から外された。なぜなら、それらは 数が少なく、また、分布にむらがあるからである。 | D(r) の値は、103pc3 当たりの星数である。括弧 は不確定性を示す。 |
|
図6a-d にはスペクトル型別に太陽から 1 kpc 以内の星の分布を示す。
分布の主な特徴を下に記す。
B8 - A0 星 B8 - A0 星は lI = [60, 120], つまり lII = [93, 153], r < 500 pc に固まっている。 A2 - A5 星 A2 - A5 星は同じ銀経区間に固まるが、もっと遠くまで伸びている。 F0 - F5 星 F0 - F5 星は、ほぼ全ての銀経で急速に減少する。例外は lI = 42, lI = 97、つまり lII = 75 と, 130 である。LF5 で 示された太陽付近での極大と窪みの存在は怪しい。 F8 - K3 星 B8 - A0 星が固まっていた領域で F8 - K3 の黄色巨星が多い。 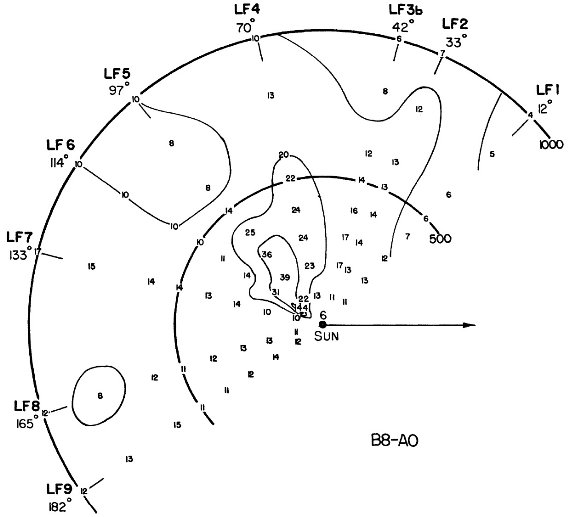 図6a.太陽から 1 kpc 以内の B8 - A0 星の空間密度。数字は 105 pc3 当たりの星数。矢印は lI = 327° 方向 (銀河系中心) 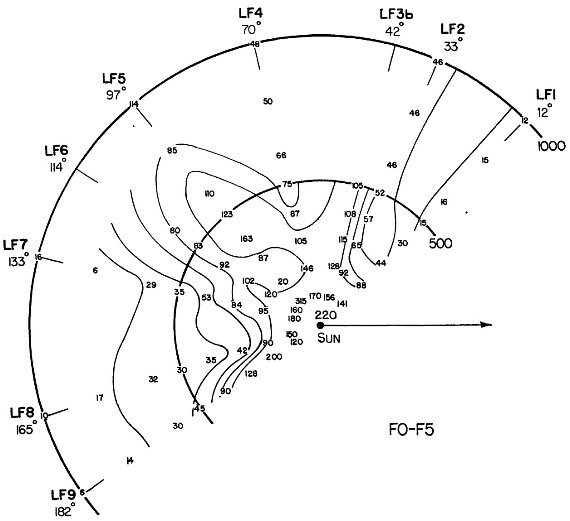 図6c.太陽から 1 kpc 以内の F0 - F5 星の空間密度。 |
Pannekoek 1929 の研究 他の研究と比較する際の問題は、スペクトル型のくくり方が異なることである。 例えば、 Pannekoek 1929 では HD カタログから B8 - A3、K0 - K8 星を選んだ。 距離限界は 300 pc で、大きくはシグナス集団の方向に A 型星の集中が見られた。 彼は A-型星と K-型星の集中に一致を認めなかったが、我々は二つの集団が 大きな空間規模で一致した分布を示すことを見出した。 Malmquist, Hufnagel 1933 HD カタログの A0 - A5 星の分布を調べ、やはりシグナス方向に 図6b にあるような 集中が r = 800 pc まで伸びることを見出した。 牡牛座の集団 牡牛座の A 型星集団は LF 領域から外れているので分布図には現れない。 しかし、McCuskey 1941 はその方向 250 pc に B8 - A3 星の集団を見出している。 注意しておくが、Pannnekoek 1929 も Malmquist, Hufnagel 1933 も星間吸収の補正は 施されていない。 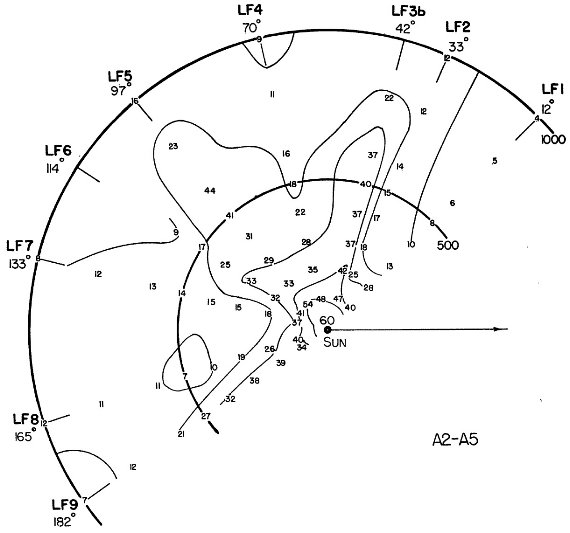 図6b.太陽から 1 kpc 以内の A2 - A5 星の空間密度。 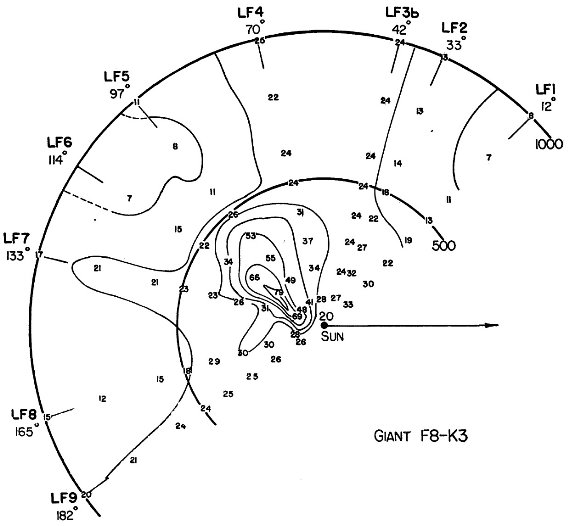 図6d.太陽から 1 kpc 以内の F8 - K3 星の空間密度。 |
|
A, B 型星の分布と渦状構造 図7a, b は B8 - A0 星と B5 星の分布を示す。lI = [130, 180], つまり lII = [163, 213] の区間には r = 1 - 2 kpc のところに 高密度領域がある。そこの星密度は太陽近傍の 4 - 5 倍である。A 型星のこの 集団は Morgan 1955 が示した局所腕とペルセウス雲の分岐点にあたる。この 領域で、 Morgan, Whitford, Code 1953 は青色超巨星の集団が集中していることを発見した。シグナス方向、局所腕に 沿ってはしかしながら A 型星の密度は低く、距離と共に減少していく。 lI = 100, つまり lII = 133 の局所腕とペルセウス腕 の中間領域では早期 A 型星の種族は非常に少ない。この研究では A 型星が渦状腕構造に付随している証拠は明らかではない。 電波観測との比較 A 型星が LF8, LF9 領域 方向で高密度であるのは、van de Hulst, Muller, Oort 1954 による HI 21 cm の観測結果とも一致する。その上 LF4, LF5 方向で r = 1 - 2 kpc に A-型星が少ないことも電波観測と合う。ただし、 r = 2 - 3 kpc に水素は大きな増加が見られるが A 型星に増加は認められなかった。 全体としては 早期 A 型星の分布を全体として述べると、0.05 星 10-3 pc3 の一様な密度の上に、反中心方向に 2 - 3 倍の密度超過が 乗っている。H-ガスに示される渦状腕、O-アソシエイション、早期 B-型星 の分布との相関ははっきりしなかった。 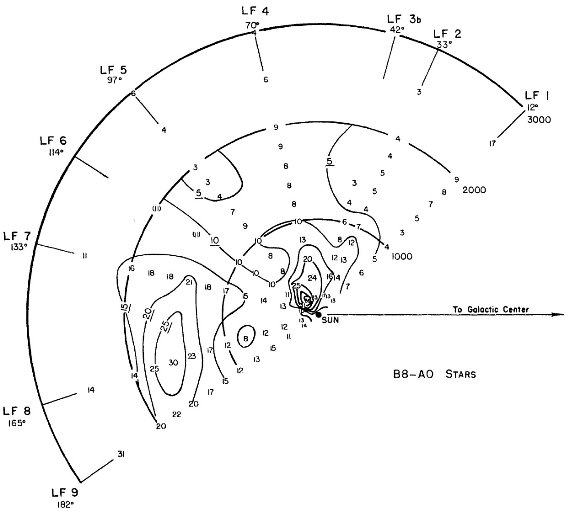 図7a.B8 - A0 星の大規模分布。密度の高い箇所と低い箇所が区別できる。 数字は、105pc3 当たりの星数。 |
B5 星分布の特徴 図7b に示されるように、 B5 型星は LF5 と LF7 領域で多い。 lI = 97、lII = 130 の密度超過は r = 2 kpc まで 伸びている。一方、lI = 133、lII = 166 の密度超過は r = 1 kpc までである。 Weaver 1953 によると、この論文で B5 星の集合が発見された辺り、 lI = [70, 100], lII = [103, 133], 方向で 早期 B-型星の集合がある。しかし、LF 7 方向の近距離に見つかった B5 星の 集合は Weaver 1953 の早期 B-型星分布では窪みに当たる。早期 B-型星が LF 1, LF 2 方向で 欠乏していることは注目に値する。これは表1にはっきり出ているし、 B5 星に対しては図7b に明らかである。Nassau, Morgan 1951 が研究した 高光度の OB-星もこの方向では数が少ない。この 2 領域の方向, lII = 45, 66 は Morgan, Whitford, Code 1953 が示したように、二つの渦状腕の中間にあたる。 一般光度関数 φ(M) 表7の密度関数を使って、各 LF 方向、距離 100, 200, 400, 600 pc における 一般光度関数を作った。Ds(r) = 距離 r におけるスペクトル型 s の密度、φ(M) = 絶対等級 [M-0.5, M+0.5] 区間にある星の数/pc3 とすると、
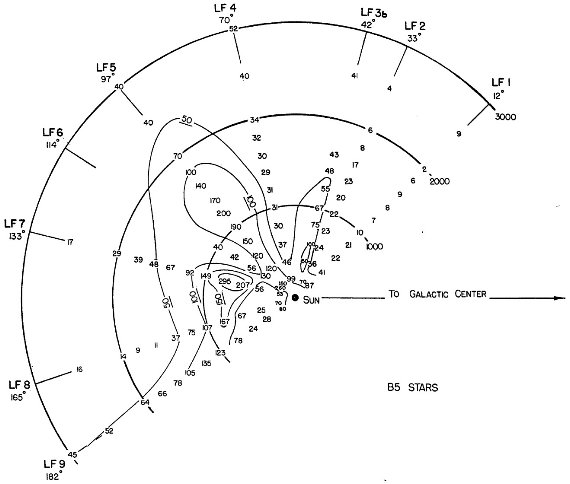 図7b.B5 星の大規模分布。数字は、107pc3 当たりの星数。 |
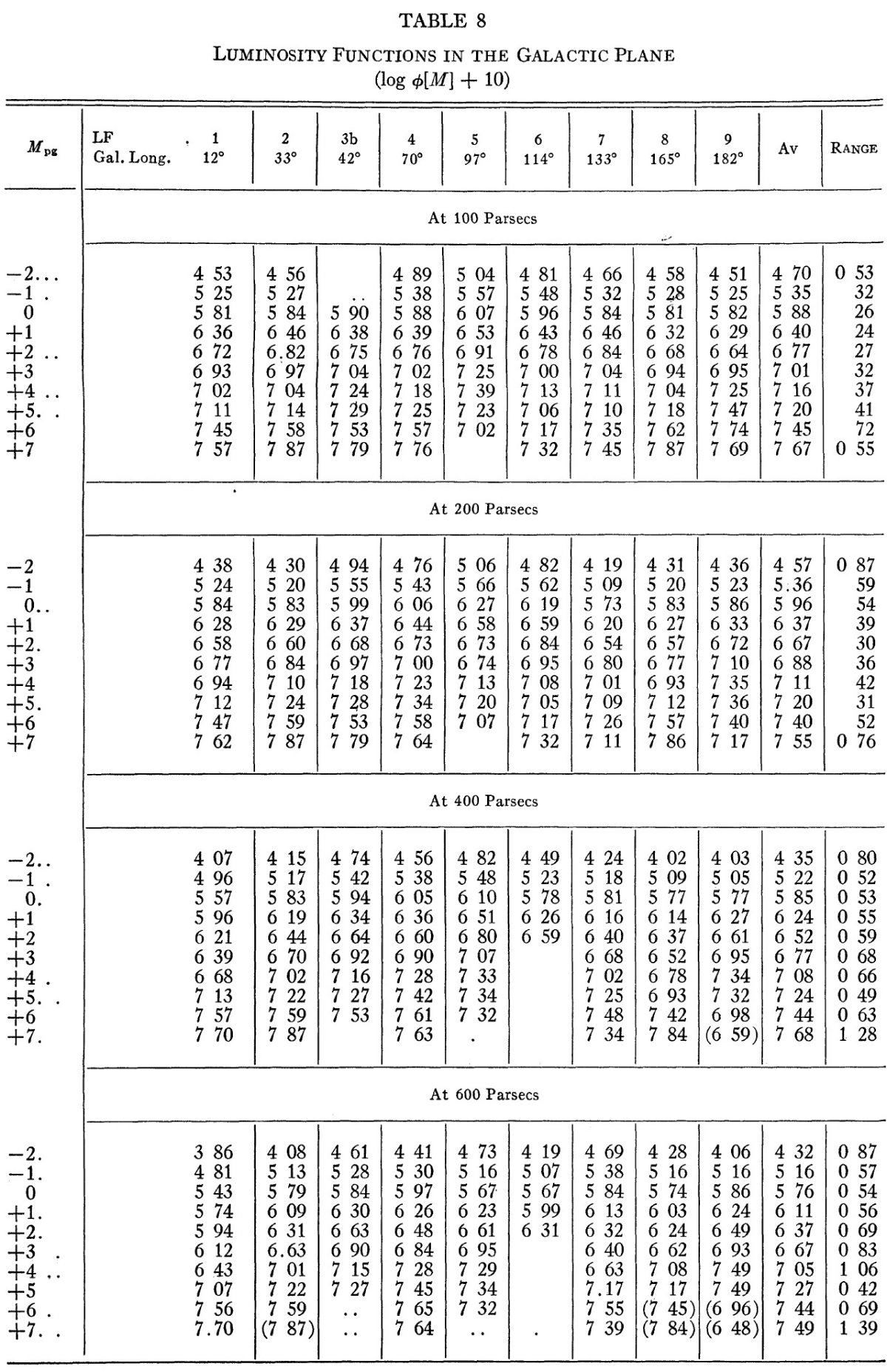
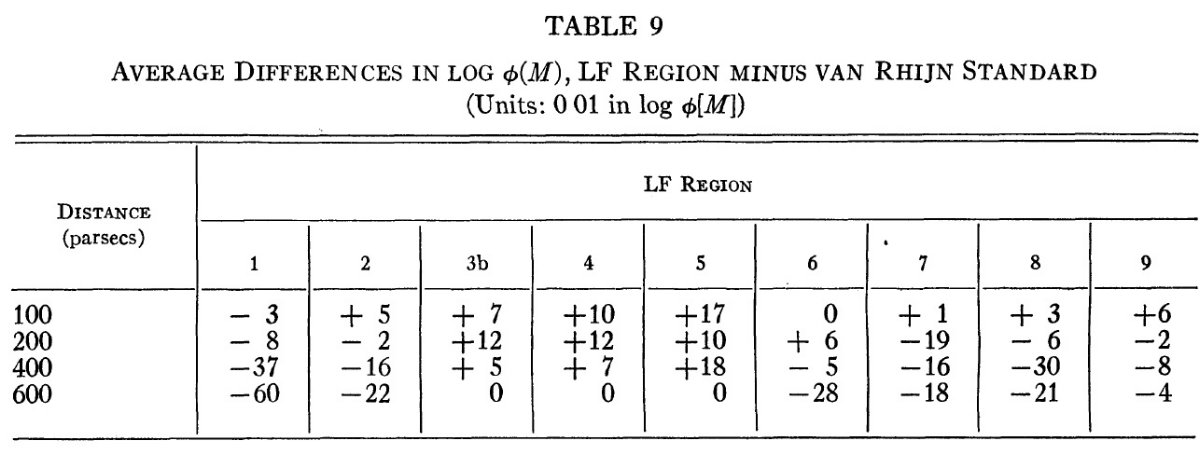
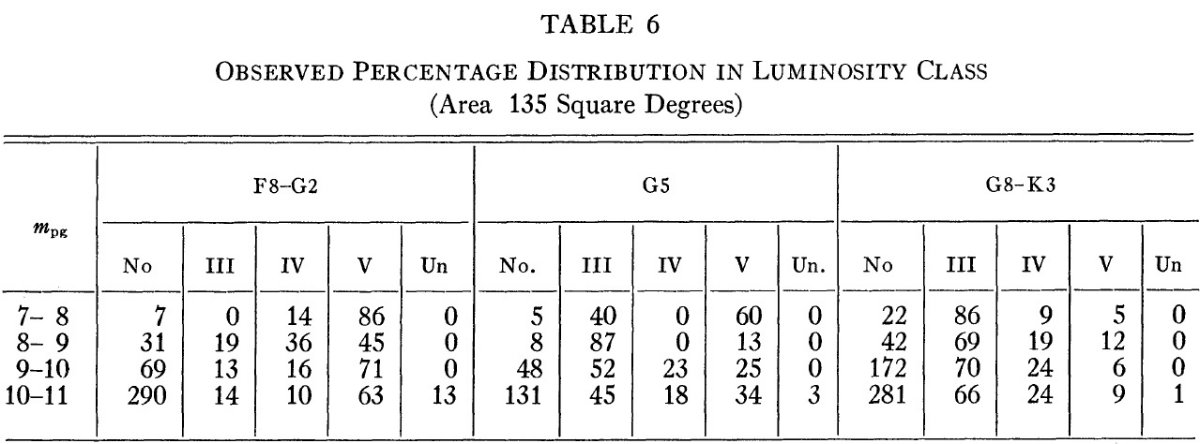
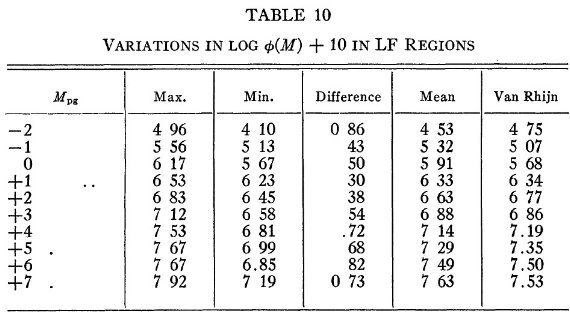 表10.LF 領域における log φ(M)+10 の変動 表8:観測光度関数 表8には log φ(M) の値を示す。計算のために、 r = 400, 600 pc では 矮星の数は外挿値を使用したので値が不確定なため、括弧に 入れた。表最後の2列は、方向全体の平均値とその変動幅を示した。 表9:観測光度関数と標準関数との差 表9には、観測光度関数と van Rhijn 標準関数との差を示した。 表10:光度関数の最大、最小値 表10には log φ(M) の最大、最小値とその巾、を載せた。 第5、第6列は、最終の平均光度関数と標準 Rhijn 関数である。 図8:光度関数の比較 図8には以上の結果をまとめて図示した。図の上の方の曲線は、4つの方向 の平均 "reduced functions" である。全 LF 方向の平均曲線は 下の方に、 van Rhijn 曲線と並べて示した。 log φ(M) の変動 500 pc 以内では log φ(M) の変動は 0.6 である。これは与えられた 等級での星の相対比がファクター4くらい変動することを意味する。図8が 示すように、 M > +3 で変動が最も大きい。 van Rhijn 関数との比較 平均光度関数と van Rhijn 関数との差は小さい。van Rhijn 関数と較べると LF 領域では、M = [-1, +1] が超過している。 この研究では等級とカラーの精度、スペクトル型分類の整合性に注意した。 したがって、Ds(r) が方向と距離で変化したのは、実際に銀河の 中で相対比が変わっているためと思われる。 |
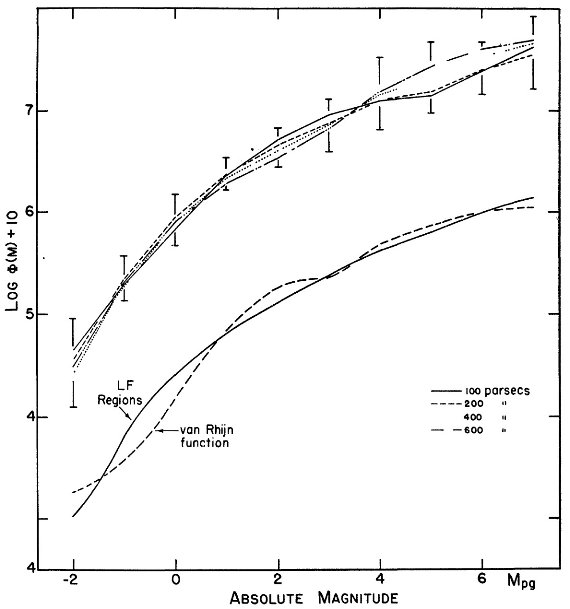 図8.log φ(M) + 10 の変化。上図は r = 100, 200, 400, 600 pc での平均光度関数。縦線は log φ(M) の巾。 下図は全領域の平均カーブと van Rhijn 関数を示す。 したがって、 結論 (1)van Rhijn 関数は太陽から 500 pc 以内の平均としては良い表現である。 (2)log φ(M) には最大で 0.6 に達する揺らぎがある。 (3)太陽近傍研究には表8に与えた数値の方が平均値よりも有用であろう。 |