Asymptotic Giant Branch Evolution at Varying Surface C/O Ratio;
Effects of Changes in Molecular Opacities

　アブストラクト　

　１．イントロ　

　２．オパシティの計算　　

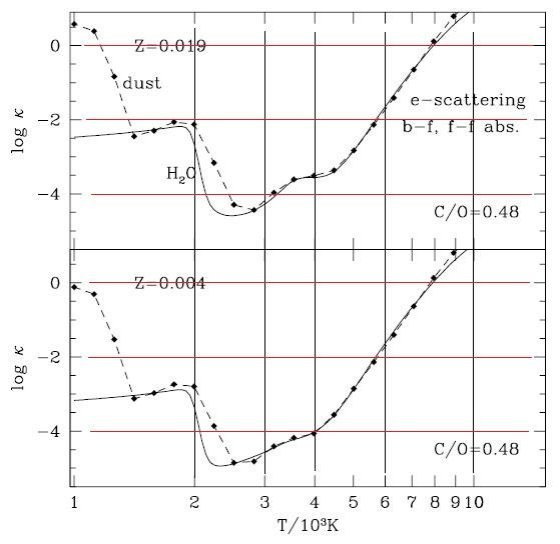
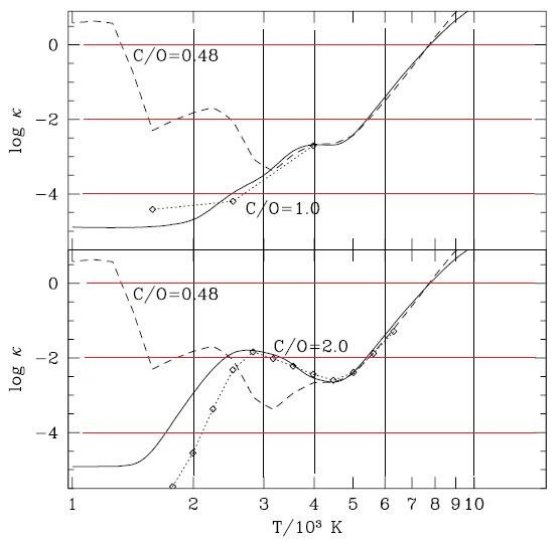
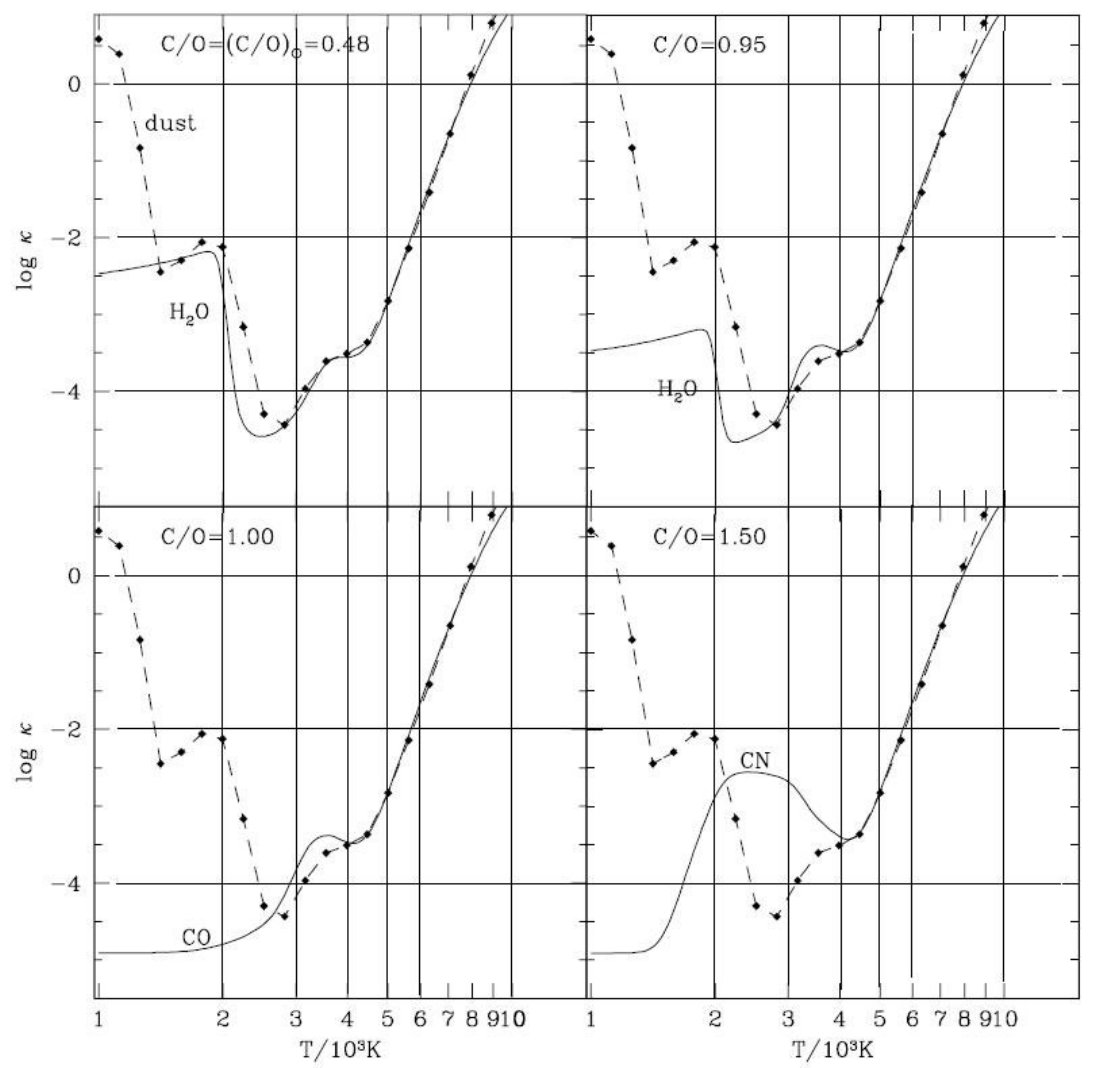
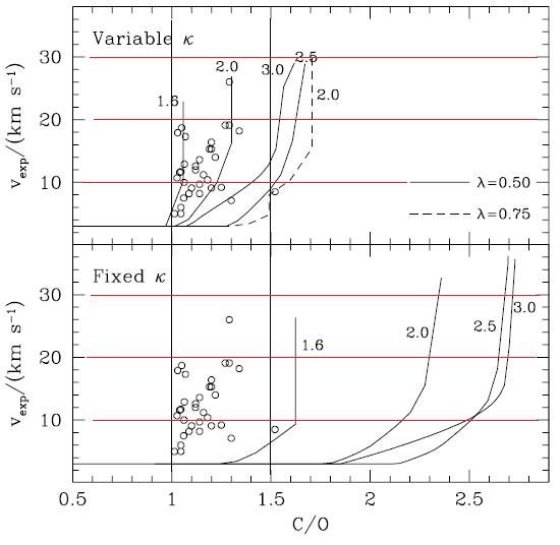
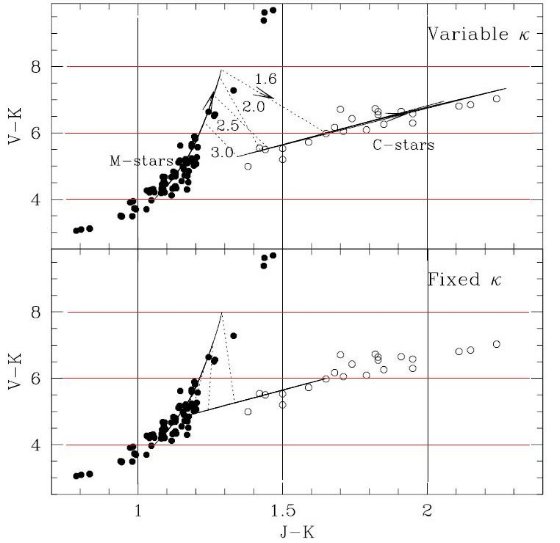
計算の概略　 　質量吸収係数 κ(cm2grsup>-1) は Keeley 1970 による、ガス密度、温度、元素組成でパラメター化された解析的関係を使う。 このフィッティング式は原子と分子の寄与を考慮している。考えられている 分子は H2, H2O, OH, CO である。元々の H2O 項は最近の研究結果に合うよう改められた。これに Scalo, Ulrich 1975 の CN 多項式フィットを加えた。最後に C2 の寄与を CN と大体同じくらいと して加えた。（Querci et al 1971） 　ロスランド平均　 　総ロスランド平均 κ を求める式は以下の通りである。 　　　　　κ = κC + ΣXiκ i 　　（１） ここに、 κC は連続吸収、 κi は i-種分子 の単位質量当たりロスランド平均オパシティである。ロスランド平均は調和平均 なので、この式は本当は正確でない。しかし、実際の場合はどれか一つが独占的 なので、誤差は大きくならない。 　２．１．分子密度　 　化学平衡の定数　　 　与えられた密度、温度、元素組成の下での原子、分子の割合は化学平衡の 式を連立させて求められる。方法は辻 1966 を見よ。 電子は H, He, C, N, O と他の主なメタルの電離を考慮して求められる。 原子の分配関数は Irwin 1981, Sauval, Tatum 1984 から取った。解離 平衡定数は Rossi, Maciel 1983 の解析的表現の助けを借りて評価した。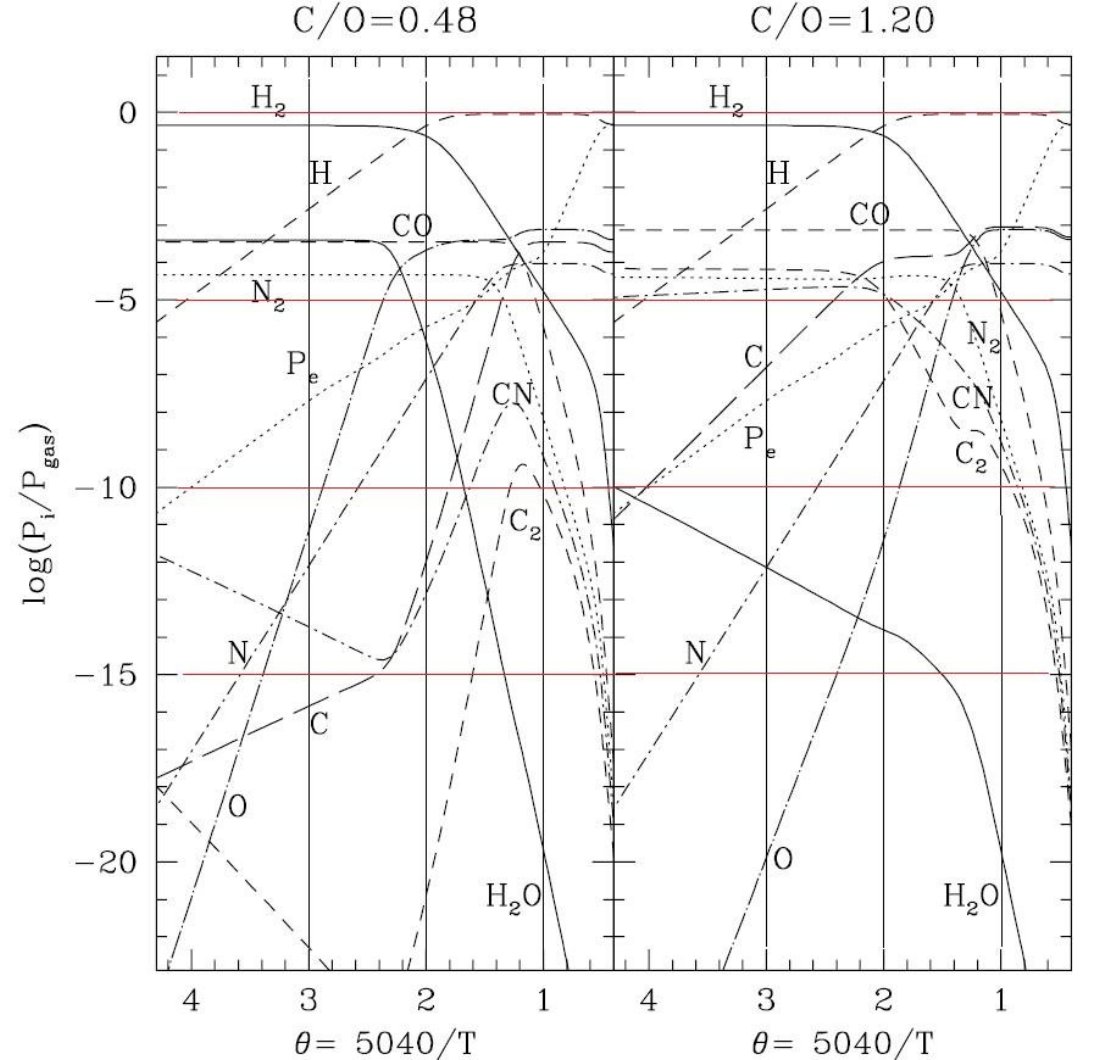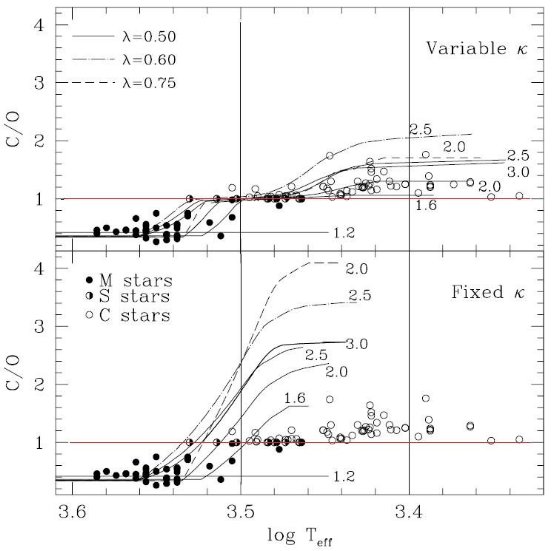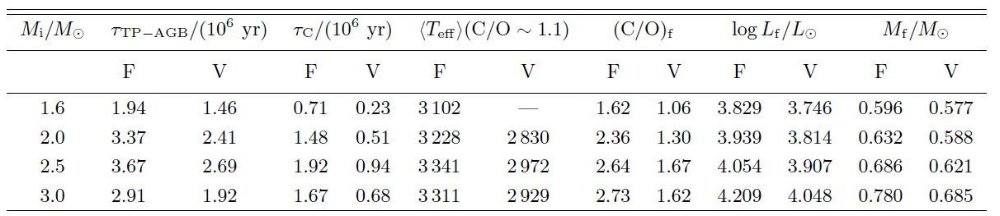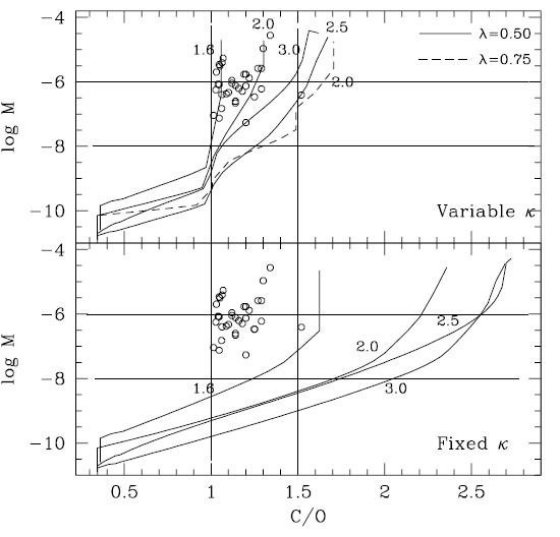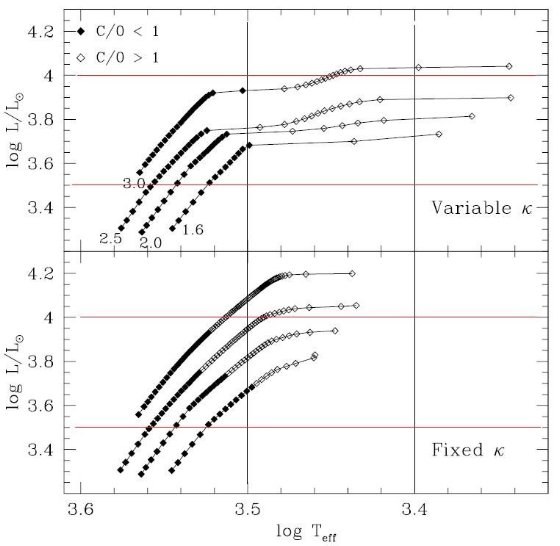 　解離平衡　　 　CO の結合エネルギーは強いため、CO を作った残りの原子から他の分子が 作られる。これは Russell 1934 が指摘した特徴である。図１を見ると、 C/O が 1 を越えた途端に CN と C2 が増加し、 H2O が減少する。同じ効果は図２にもはっきり表れている。また、 2000 K 以下 では H 原子が減り、H2 分子が支配的になることも注意したい。

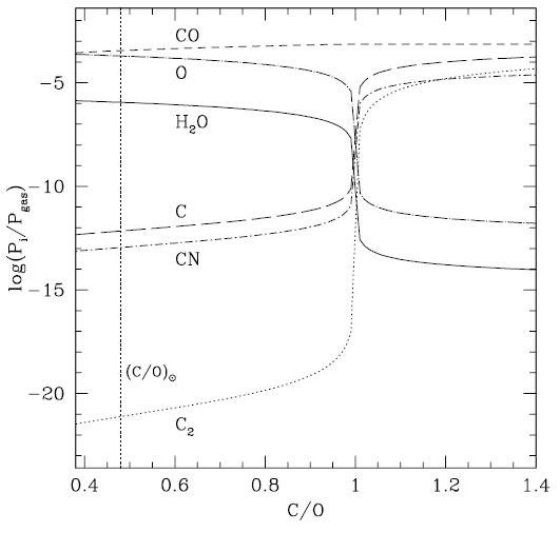
図１．Pgas = 103dyne cm-2, T = 2500 K での 分圧と C/O 比との関係。縦線は太陽組成 C/O = 0.48 を表わす。

２．２．他のオパシティデータとの比較　 　C/O = 0.48 (スケール太陽組成) での比較　　 　図３では、良く引用されている ALexander,Ferguson 1994 の結果と比較した。 そこでは、C/O = 0.48 が固定されたすけーる太陽組成が採用されている。図では 二つの例、[Y=0.273, Z=0.019] と [Y=0.240, Z=0.004]、が示されている。どちらも 付随する密度は log R = log ρ + 3(6-log T) = -3 で与えられている。ここで R はオパシティテーブルの内挿が滑らかに進むよう良く使われる量である。 　本論文と ALexander,Ferguson 1994 との一致は良い。特に、 T ≤ 2500 K に 現れる水蒸気によるオパシティのこぶがうまく表現されている。 ALexander,Ferguson 1994 ではこの論文には含まれていない TiO による寄与も示されている。 とにかく、 Keeley 1970 の式では水蒸気のオパシティが小さく見積もられ過ぎている。 我々はこの項を修正した。T ≤ 1500 K の第２のこぶはダストによるもので、我々の 計算には入っていない。 図３．Z = 0.019, 0.004 で C/O = 0.48 のロスランド平均オパシティ温度変化。 　　　各温度に対応する密度は、log R = log ρ + 3(6 - log T) = -3 で決定。 　　　実線＝この論文。破線= Alexanderm Ferguson 1994

C/O = 1, 2 での比較　　　 　図４は C/O = 1 Alexander et al 1983、C/O = 2 Lucy et al 1986 との比較である。 O-組成は太陽とした。どちらも、T < 4500 K でスケール太陽(C/O=0.48) から ずれていく。この原因は C/O = 1 では水蒸気がなくなることであり、C/O = 2 では CN が出現するためである。我々のカーブもいくらかの差はあるがこの基本的な 特徴は再現している。 　我々の方法の有用性　 　このように、我々の方法は C/O が変化する場合に一貫して使用可能なオパシティ を与えることが判った。 TiO は効かないのか？　κC はどう与える？ 図４．幾つかの C/O 比で、オパシティの温度変化。log ρ = -9 仮定。 　　　上：C/O = 1.0 実線=この論文。点線=Alexander et al 1983. 　　　下：C/O = 2.0 実線=この論文。点線=Lucy et al 1986. 　　　比較のため C/O=0.48 Alexander,Ferguson 1994 破線。

　４．M-型星とC-型星の有効温度　

M-型星とC-型星の有効温度　 　星のモデル計算から、光度 L が与えられている時にオパシティが大きくなると 半径も大きくなることが判る。これは、Teff = 2000 - 4000 K で C-リッチ大気が CN コブの極大、 O-リッチ大気がオパシティ極小になり、C-リッチモデルが低温 になることを説明する。ちょっと循環論法ぽいな。 　観測有効温度　 　この予言は C/O 比と有効温度の相関を上手く説明する。この傾向は図６に示さ れている。サンプル炭素星の有効温度のほとんどは、干渉計または月の掩蔽による 視角測定に基づいており、現在最も信頼できるデータと言える。データの収集に 関しては Bergeat et al 2001 を参照。M-型、S-型の有効温度はスペクトル解析に 基づいている。図６を見ると次の点が明らかになる： （１）O-リッチ星と C-リッチ星の有効温度が完全に分離する。 （２）C/O 比が <2 で案外小さい。 　F-合成モデルと観測との比較　　　 　図６下を見るとスケール太陽モデルが観測と不一致なことが判る。F-モデルは 有効温度が高く、C/O 比が大きい領域にいて、観測点に達しない。また、 表面 C/O 比が増加するにつれ log Teff の減少はほぼ直線状に変化して行き、 ある点からはより激しく低下する特徴を示している。F-モデルでは C/O 比が 1 を越す際にも Teff の変化率に変化は見られない。これはF-モデルではそこで 分子オパシティに大きなジャンプが生じないので当然である。最後に温度低下 が急になるのは超星風で外層質量が急減することに付随している。 　V-合成モデルと観測との比較　 　V-モデルは観測とモデルの一致が良い。F-モデルと違い、V-モデルは C/O 比 が 1 を越すや否や有効温度が大きく低下する。これは、CN と C2 の出現が原因である。そして、大気の温度低下はマスロス率の増加をもたらし、 超星風の発生に導いた。 　F-、V-モデルの差　 　図６の温度低下曲線の平坦部分は F-型と V-型とで理由が異なる。F-型では 平坦化は外層マスの低下が原因である。そしてその発生は炭素星への転化が 済み、超星風が起きた時である。一方、モデル V ではM-リッチ星からC-リッチ 星への転化に伴う分子オパシティの大きな増加が平坦化の原因である。この 特徴は TP-AGB 進化を図７の HR-図で見ると良く分かる。モデルFに較べると、 モデルVの低温度化は低光度で起き、より低温側に伸びている。 　もう少し詳しく見ると、炭素星への転化に伴う大きな温度低下の後は温度 低下スピードが緩やかになり、最後に超星風開始に伴い再び大きな温度低下 が見られる。

図６．銀河系巨星の C/O に対する有効温度の関係。組成と有効温度は Smith, Lambert 1985, 1986, 1990 (M-型星), Ohnaka,Tsuji 1996 (S-型星), Lambert et al 1986、Ohnaka et al 2000 (C-型星)。ただし、炭素星に関しては Bergeat et al 2001 の表を採用した。 なぜだ？ 曲線はモデル。上＝その場計算オパシティ。下＝スケール太陽オパシティ。 　Vモデルの総括　 　C/O < 1　では Teff の領域はせまい。C/O ∼ 1 では　Teff の巾は大きくなり、 C/O > 1 になると、Teff はさらに低下する。Teff は星の色々なパラメター が効いてくるので、C/O が大きくなると同じ C/O でも　Teff の分散は大きくなる。

　５．他の進化及び観測的効果　

種々の観測量　 　第４章で述べた有効温度以外にも V-モデルは他の観測量をも上手く説明する。 まず表１を見ると、V-オパシティは炭素星寿命を 1/2 - 1/3 に切り下げること が判る。既に述べた通り、これはC-リッチになった途端に低温化し、それが超星風の 発生を速めたことに起因する。 　この他に AGB 終端光度と終端質量も影響を受けた。図７を見ると、同じ質量で 較べた時、V-モデルでの光度範囲はモデルFよりずっと狭い。その結果、Lf, Mf は 低くなった。図７を見ると、炭素星光度と初期質量の関係が良く決まることに 気付く。その上、初期質量 - 終端質量関係は平坦化する。しかし、この点を 調べる前に他のパラメター λ などが再較正される必要がある。基本的な 較正量はマゼラン雲の炭素星光度関数と白色矮星質量関数である。 　質量放出率　 　図８を見ると、炭素星の質量放出率と C/O の関係が良く再現されていることが わかる。同様な関係が vexp にも成り立つことが図９から判る。 これは、Vassiliadis, Wood 1993 の処方で周期から導かれるが、この周期が 表面温度、しいては C/O と関係するのである。 　炭素星と M-型星との比　 　炭素星寿命の減少は炭素星と M-型星との比 N(C)/N(M) にも影響する。表１の 結果に基づくと、τC/(τTP-AGB - τC) を Mi の関数として表わすと、それは星団の N(C)/N(M) の目安となる。 　この論文の計算によると、この比は F-モデルでは 0.58 - 1.35 になるが、V- モデルでは 0.19 - 0.55 となる。その上、炭素原子の生産率が低下するので 惑星状星雲で見られるかなり低い C/H, C/O (Pottasch 2000;ISO)を説明するのに 都合が良い。実際、恒星が作る炭素量が低いことは銀河の化学進化からも 要請（Portinari et al 1998）されている。 　 図８．AGB 星質量放出率の C/O による変化。白丸＝観測。Loup et al 1993, Wannier et al 1990 が -(dM/dt), Lambert et al 1986, Ohnaka et al 2000 が C/O 比。実線＝モデル。F-モデルは観測と一致しない。

図７．Z = 0.19 TP-AGB モデルの HR 図上進化。ドレッジアップ効率λ=0.5 　　　四角＝各熱パルスサイクル末の前フラッシュ光度 L 　　　上＝その場計算オパシティ。下＝スケール太陽オパシティ。 図９．AGB 星シェル膨張速度の C/O による変化。白丸＝観測　Loup et al 1993.

近赤外カラー　 　分子オパシティの改良は AGB 星の近赤外カラーをよく記述するのにも役立つ。 より詳細な検討は後に残すが、O-リッチ星と C-リッチ星の間での J-K 対 V-K 二色図の二分化について簡単に述べよう。 　図１０に見られるように、M-型星と C-型星は異なる二本の枝を形成している。 モデルはその場オパシティとスケール太陽の双方を示した。温度からカラーへの 変換には Fluks et al 1994 (M-型星）と Bergeat et al 2001 (C-型星) を用いた。 　炭素星　 　炭素星の枝に関して、その場オパシティのモデルは観測される J-K の領域、1.3 - 2.3, を完全に通過する。一方、スケール太陽モデルは青いまく　J-K < 1.7 に 留まる。　 　将来の方向　 　観測とのより詳細な比較が必要であることは明らかである。そのためにはドレッジ アップ効率とのパラメターの再較正が必要である。いずれにせよ、この試験的な 計算だけでも、新しいその場オパシティが正しい方向を目指していることは 明らかである

図１０．太陽近傍の M-型星と C-型星の近赤外２色図。黒丸＝M-型星データは Fluks et al 1994、白丸＝C-型星データは Bergeat et al 2001 より。実線＝ その場計算オパシティ（上図）とスケール太陽オパシティ（下図）モデル。

　６．結論