Keck II 搭載の DEIMOS 多天体ファイバー分光器による速度データ(CaT使用)
を用いて、M 31 厚い円盤の特性を初めて示す。M31 南西部 21 領域で
薄い円盤に対して厚い円盤成分が遅れていることを見出した。また、速度
分散、メタル量、スケール長にも差があった。速度差 ⟨ Δv
⟩ = 46.0 ±3.9 km s-1 であった。
メタルは、[Fe/H]=-2.66+0.42[∑Ca+0.64(VRGB-VHB)]
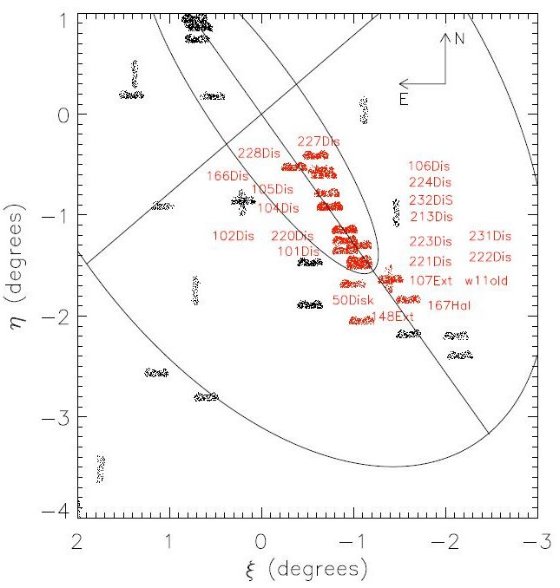
図1.観測領域。赤=今回使用。外楕円= 55 kpc 円を c/a = 0.6 で投影。 内楕円= 2° = 27 kpc 円の投影。
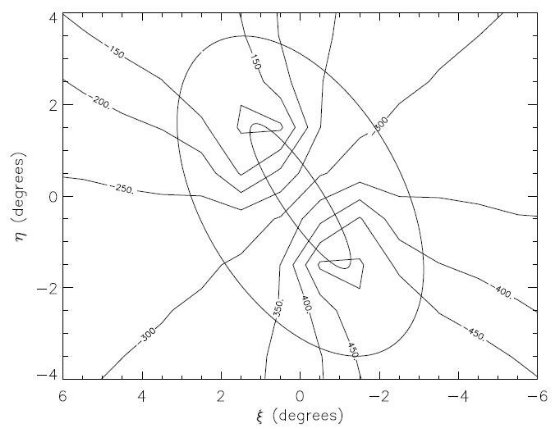
図4.円盤回転曲線から期待される視線速度分布。
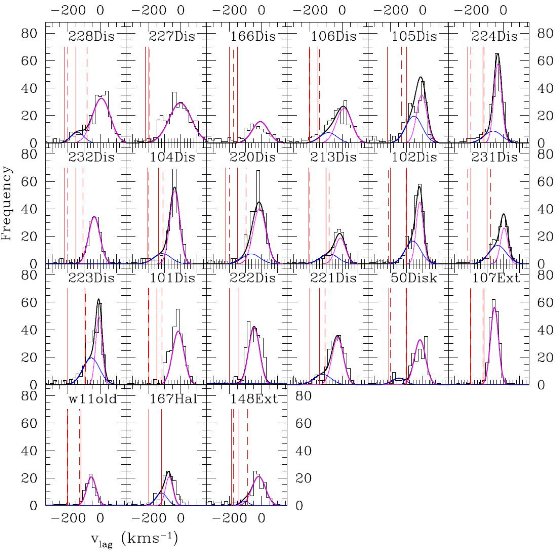
図6.フレームは中心距離の順。マゼンタ=円盤、青=厚い円盤へのガウシャン フィット。厚い円盤星の選択区間は、破線=薄い円盤の 2 σ の先を 厚い円盤としてカット、実線=ガウシャンカットで、ほぼ重なっている。
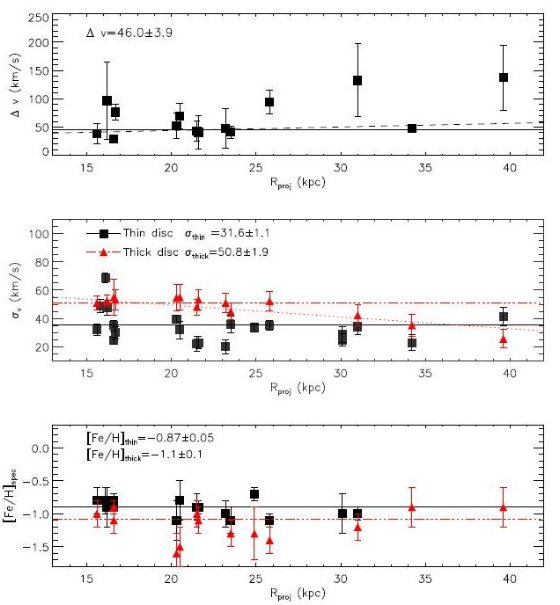
図8.(上)薄い円盤と厚い円盤との速度差 Δv の投影距離による変化が ほぼ一定の 46.0±3.9 km s-1 である。。 (中)黒四角=薄い円盤の速度分散。赤三角=厚い円盤の速度分散。 (下)黒四角=薄い円盤のメタル量。赤三角=厚い円盤のメタル量。勾配は 認められない。
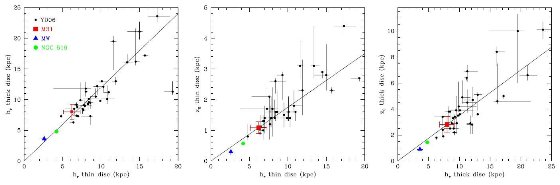
図10.(左)薄い円盤と厚い円盤のスケール長の比較。 (中)薄い円盤のスケール長とスケール高の比較。 (下)厚い円盤のスケール長とスケール高の比較。
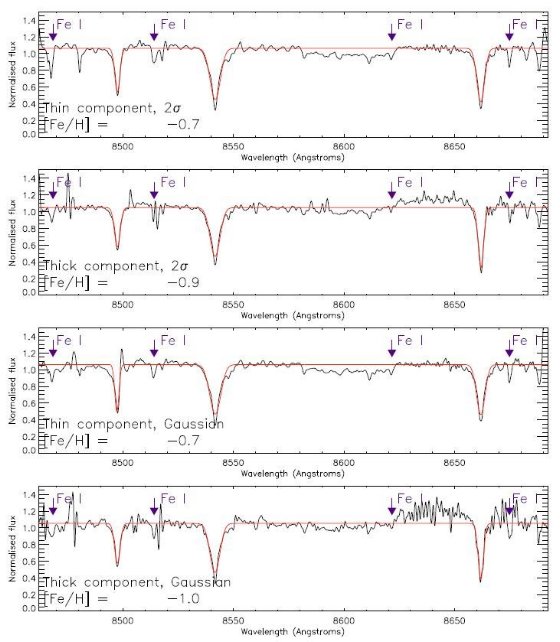
図12.2σカット(上)とガウシャンカット(下)で選別した 厚い円盤星と薄い円盤星夫々のスペクトル (S/N ≥ 3.0) の合成。 薄い円盤の平均メタル量が 0.2 - 0.3 dex 多い。
厚い円盤の速度分散は σthick = 50.8±1.9 km s-1 で、薄い円盤の σthin = 35.7 ±1.0 km s-1 より大きい。メタル量は [Fe/H]thick = -1.0±0.1 で [Fe/H]thin = -0.7±0.05 より低い。スケール長は Lthick = 8.0±1.2 kpc, Lthin = 7.3±1.0 kpc であった。ここから、スケール高 Hthick = 2.8±0.6 kpc, Hthin = 1.1±0.2 kpc を導いた。どちらも銀河系の 2 - 3 倍厚い。厚い円盤の総質量は 2.4 × 1010 Mo < Mthick < 4.1 × 1010 Mo で、 厚い円盤の形成メカニズムはこれだけの質量を「加熱」する必要がある。

図3.HI 回転曲線、
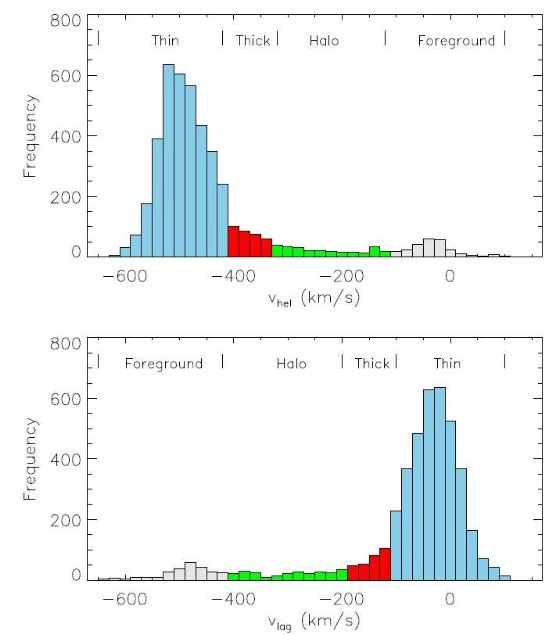
図5.全21領域星の、(上)太陽中心速度。(下)円盤遅れ速度。 青=円盤星、赤=厚い円盤、緑=ハロー、灰=銀河系星が占めていると 看做す。
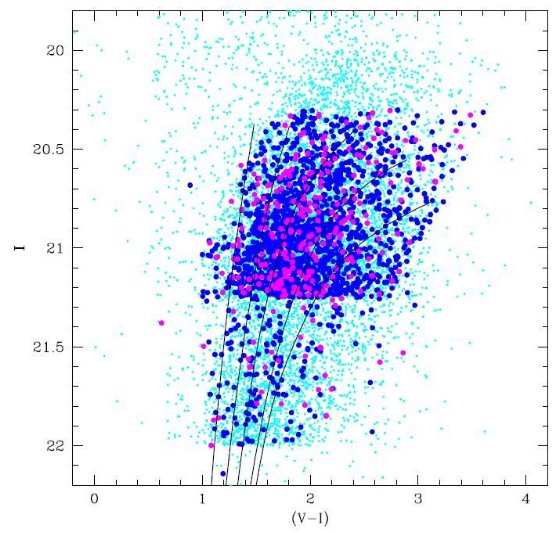
図7.青点=円盤。マゼンタ=厚い円盤。薄青=それ以外の星。 の色等級図。[α/Fe]=0.2, t = 8 Gyr, [Fe/H] = -1.5, -1.0, -0.5, -0.4 の等時線。
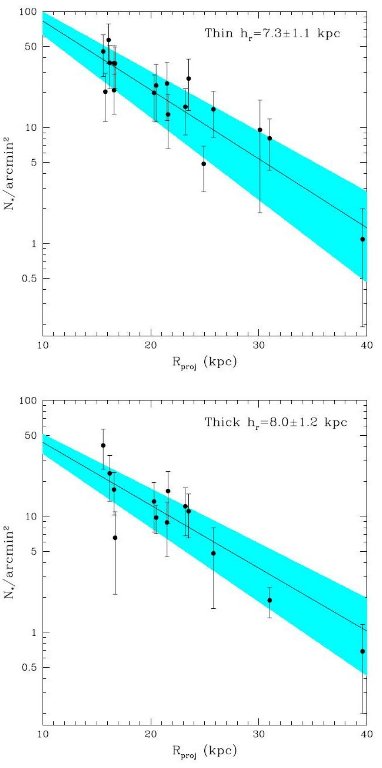
図9.(うえ)薄い円盤星のコラム数密度(N∗ arcmin 2) の中心投影距離による変化。v
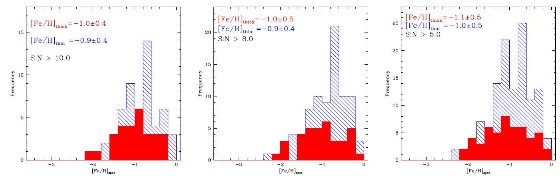
図11.青斜線=薄い円盤+厚い円盤星の分光メタル量分布。S/N 比の違い。
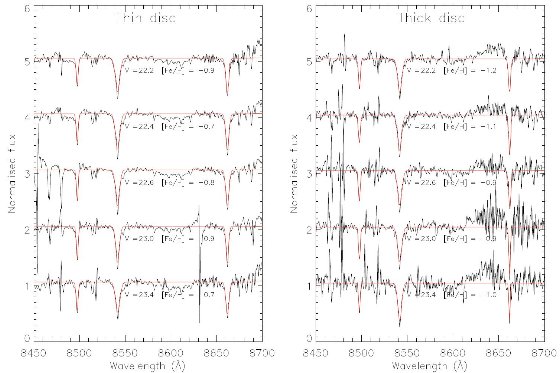
図13.(左)薄い円盤、(右)厚い円盤、のスペクトル。厚い円盤が 低メタルであることが判る。
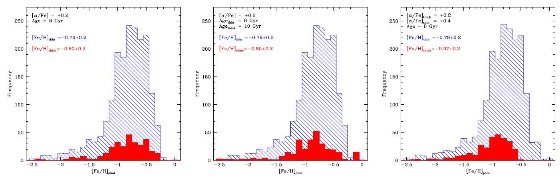
図14.等時線(図7)から求めた薄い円盤(青斜線)と厚い円盤(赤) のメタル量分布。(左)[α/Fe]=+0.2, t = 8 Gyr 等時線。(中央) )[α/Fe]=+0.2, t = 10 Gyr (右)厚い円盤の[α/Fe]=+0.4