自己整合性の円盤銀河の力学平衡モデルを作った。成分は指数関数円盤、Hernquist モデルバルジ(Hernquist 1990)、 NFW ハロー(Navarro et al 1996)、中心ブラック ホールである。モデルの各成分は密度関数 で表わされる。多数のパラメターにより現実の銀河が再現された。
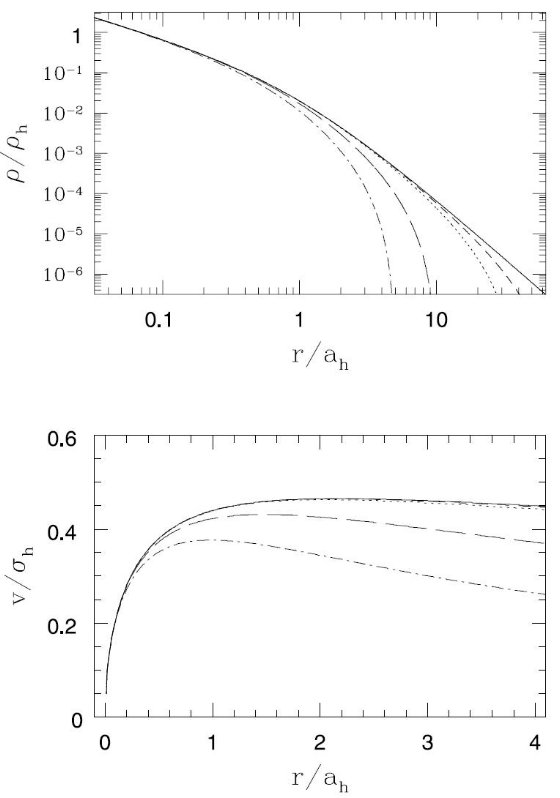
図1.ハローモデル ah = σh = 1, Ε h は rt = 5, 10, 40, 80 に対する値を取る。 (上)密度プロファイル。(下)回転曲線。
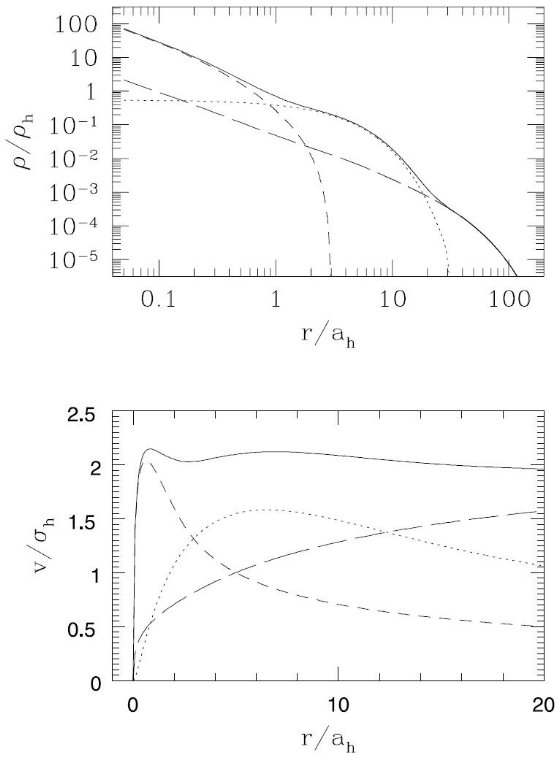
図3.モデル MWa に対する(上)密度プロファイルと(下)回転曲線。
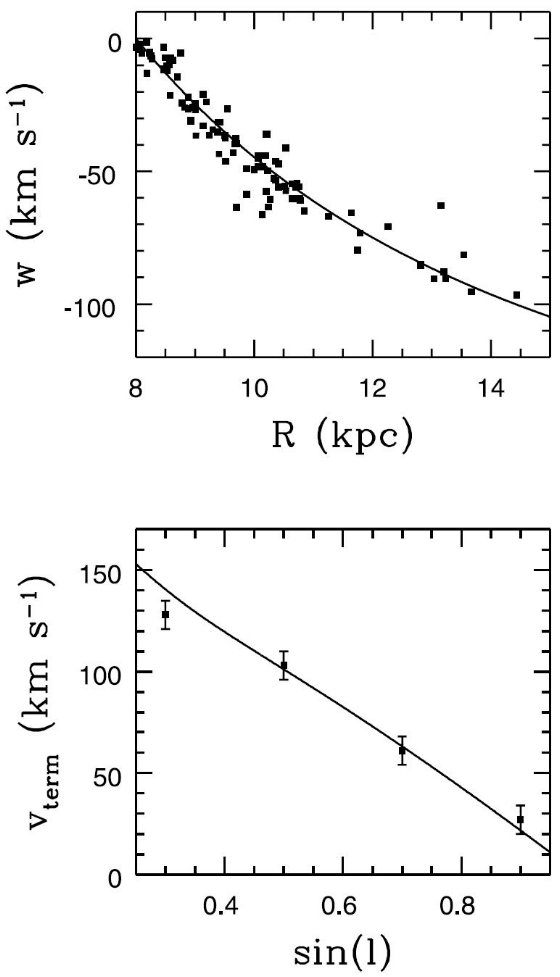
図5.MW モデルと観測値 W (上)と vterm の比較。
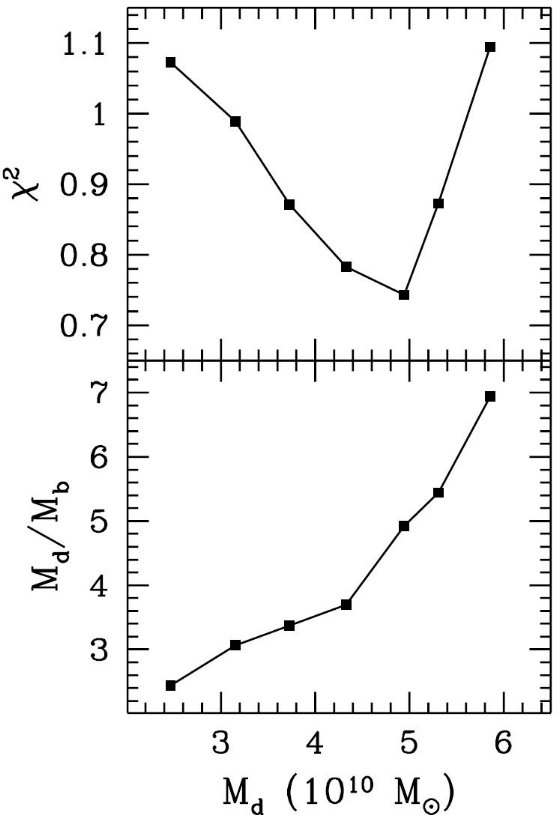
図7.Mdによる χ2 とそこでのベストフィット Mb の変化。
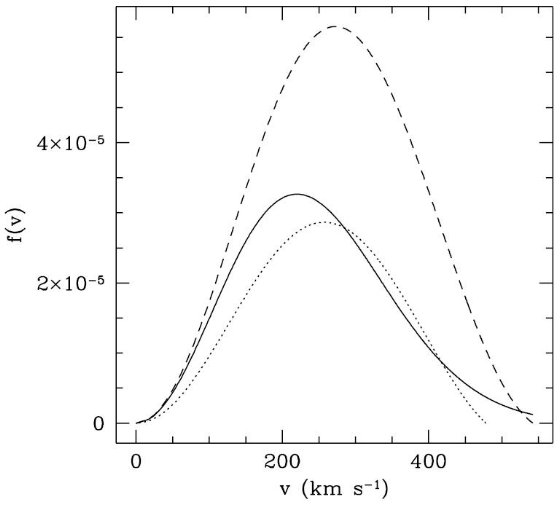
図9.M31a と M31b モデルでの太陽位置での速度分布。
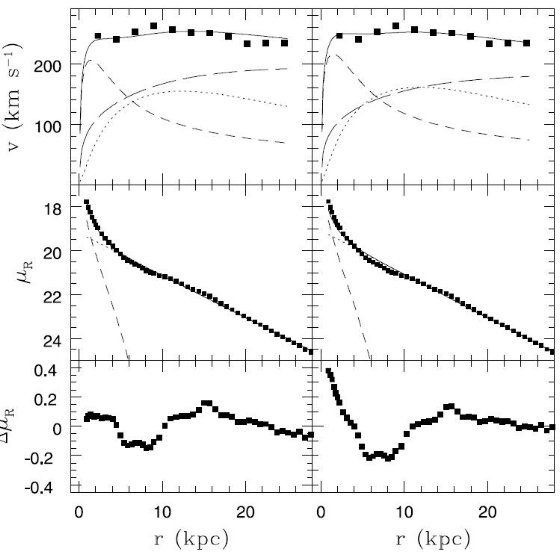
図11.(上)回転曲線、(中)R-バンド表面輝度、(下)表面輝度 残差、の(左) M31a と(右)M31b モデルでの予言と観測の比較。
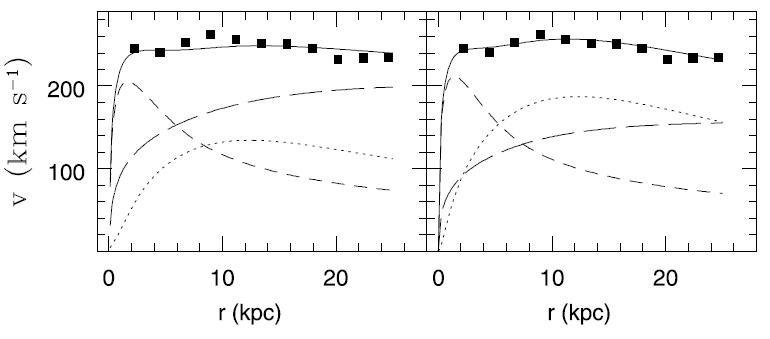
図13.M31c (左)と M31d(右)の回転曲線。
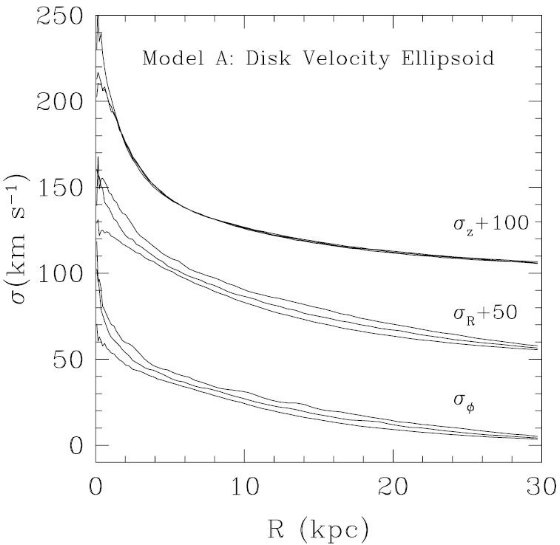
図15.10 Gyr 間の速度楕円の進化。t = 0, 2.4, 4.8 Gyr
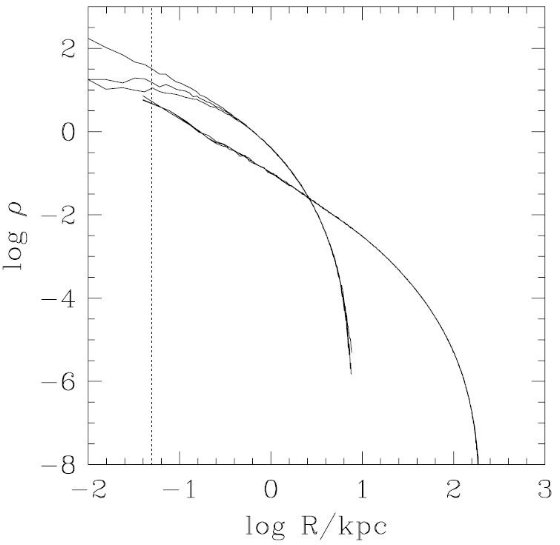
図17.バルジとハローの動径方向密度プロファイルの進化。点線は 軟化長 s = 50 pc
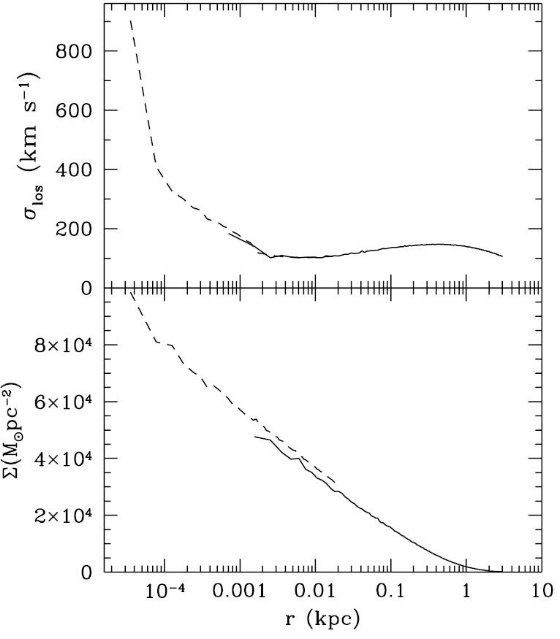
図19.バルジの速度分散(上)と表面輝度(下)。
表面輝度分布、回転曲線、バルジ速度分散などのデータから M31 と天の川銀河の ベストフィットモデルが求められた。N 体シミュレーションによりバー形成に対する 安定性が調べられた。
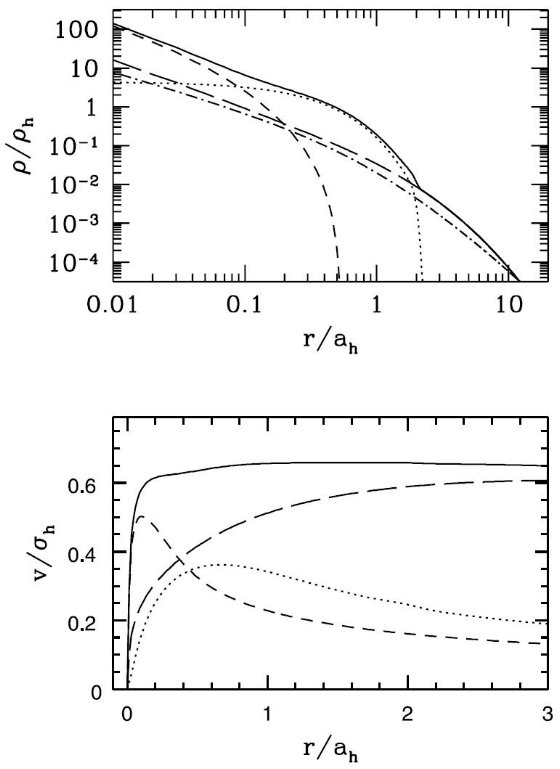
図2.本文中の円盤+バルジ+ハローモデルに対する、(上)密度プロファイル と(下)回転曲線。点線=円盤、破線=バルジ、長鎖線=ハロー、実線 =総計。一点鎖線=ハローだけの時。
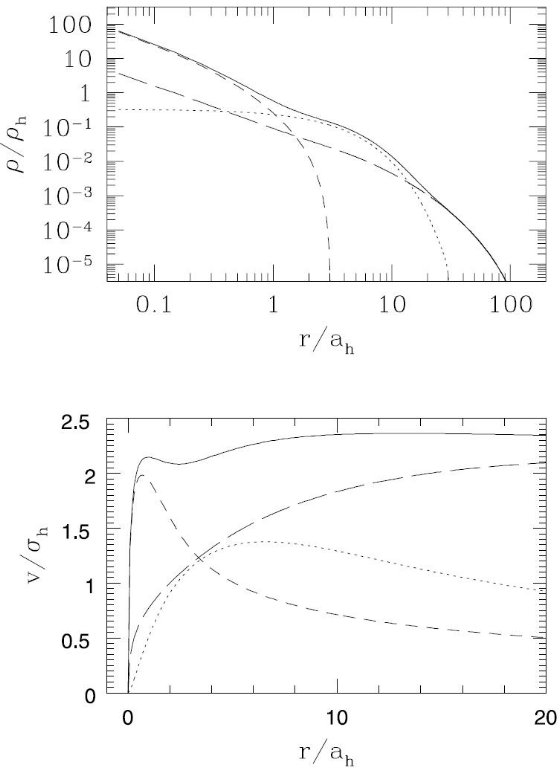
図4.モデル MWb に対する(上)密度プロファイルと(下)回転曲線。
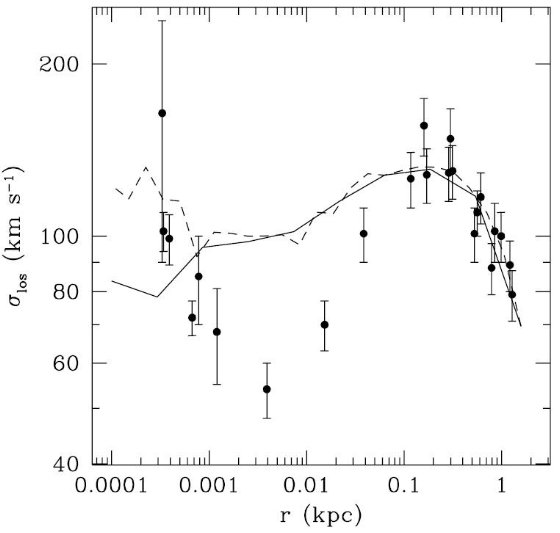
図6.バルジ方向の視線速度分散。データは Tremaine et al 2002 のデータ 収集。
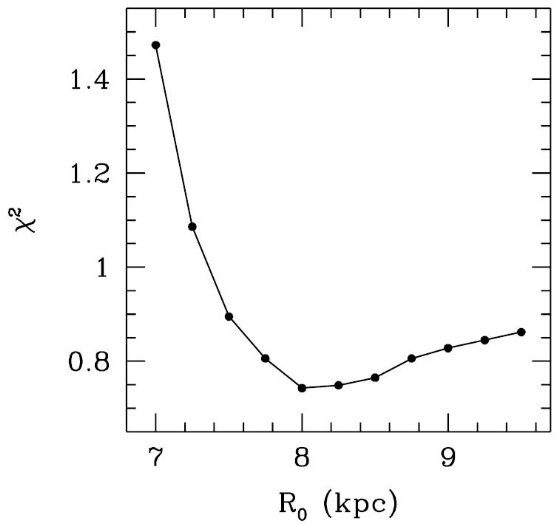
図8.銀河中心までの距離 Ro に対する χ2 。
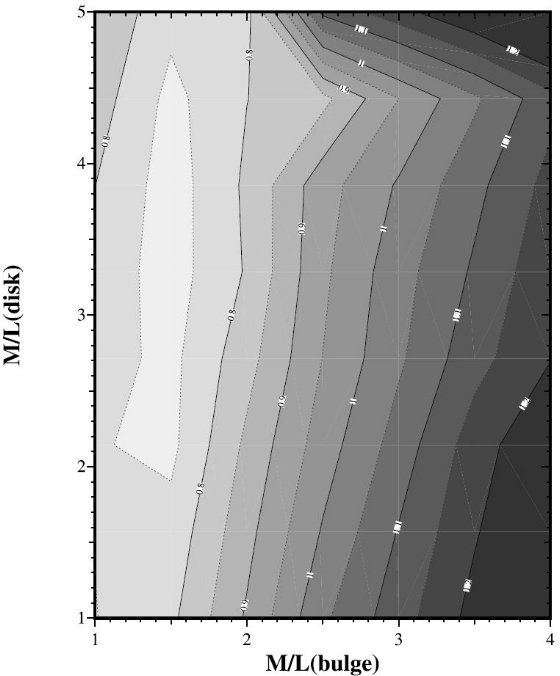
図10. χ2 等高線。
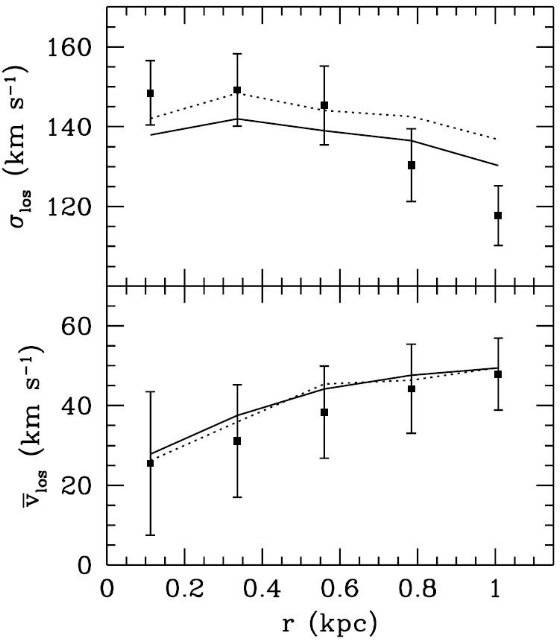
図12.バルジ速度分散と回転速度。実線= M31a, 点線= M31b, 点=観測。
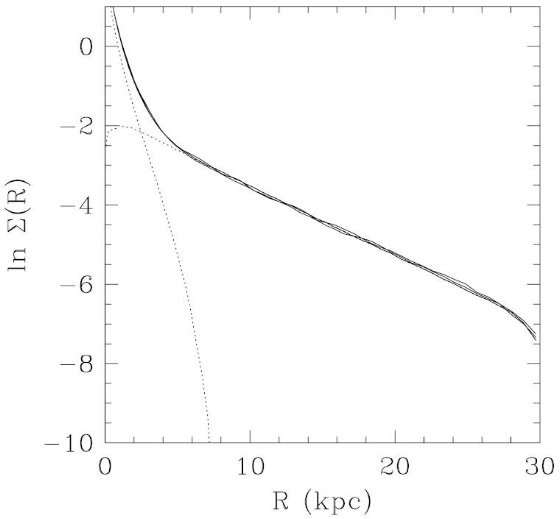
図14.4.8 Gyr に渡る表面輝度の進化。
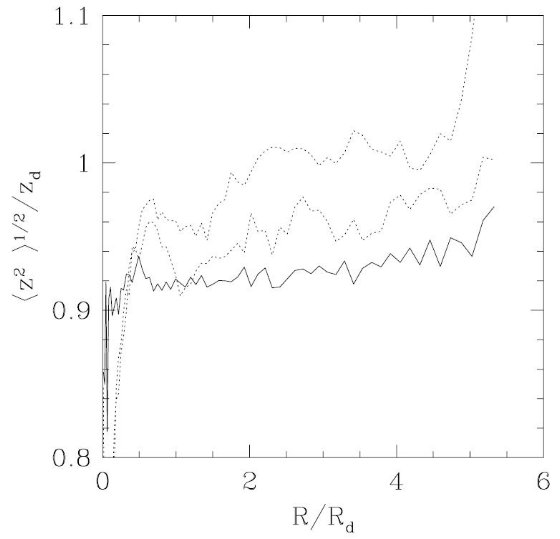
図16.円盤スケール高の進化。実線は t = 0, 点線は t = 2.4, 4.8 Gyr
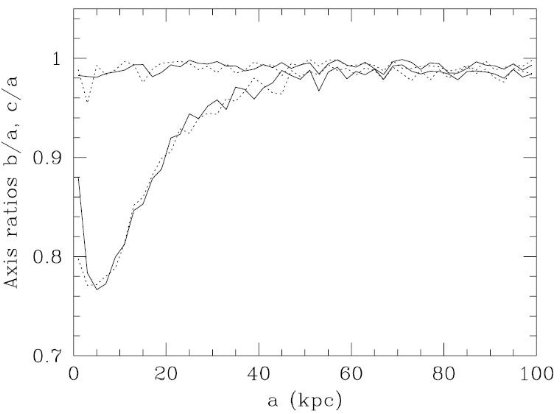
図18.ハロー軸比の進化。実線=最初。点線=4.8 Gyr。
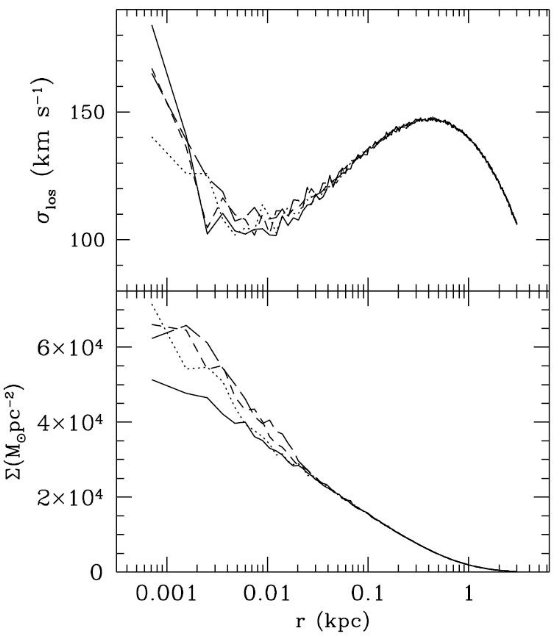
図20.ブラックホール周囲の速度分散と表面輝度の進化。