A Possible Four-Arm Spiral Pattern in the Galaxy

　アブストラクト　

　１．イントロダクション　

密度波理論が観測とモデルの比較に不可欠　 　 Yuan (1969), Burton (1971) は、観測とモデルの比較では、密度波理論が予想するストリーム運動と密度 超過の双方を考慮する必要があることを示した。この論文では、その比較に ６か所を用いる。 　可視の２方向　 　ペルセウス、カリーナ領域の可視データは、アソシエイション、星団、HIIRs で Humphreys 1972, 1976 から採った。データは l = 120 方向でペルセウス腕 までの距離を 2.5 kpc とした。カリーナ腕は同様に l = 290 で r = 3 kpc と なる。この論文では、 3.5 kpc とした。その理由は接点円が l = 290 方向で 3.5 kpc 点を横切るからである。 　腕の接点　 　渦状腕がない場合には、終端速度の点は全て接点円の上にある。ストリー ミングはデータに波状の摂動を加える。その結果、渦状腕が端点円と交差する 付近で dV/dl &som; 0 となる。接点円を空間で固定すると、この dV/dl = 0 の方向が渦状構造の位置を直接に定める。 図１．大きい破線＝太陽周円。小さい破線＝接点円。 太陽の右上＝ペルセウス腕のアソシエイションと星団。 太陽の左下＝カリーナ腕のアソシエイションと星団。 黒太線＝４つの接点領域。実線＝ここで使用した腕。 密度波とストリーミングはサイン関数的を仮定した。

　終端速度曲線のうねり　

図３a． l = [0, 90] の接点速度。黒点＝一番外側のピークから半分下がった 所の速度。実線＝モデル II (対称 4 本腕)

図３b． l = [270, 360] の接点速度。

　２．渦状構造モデル　

モデルに用いた運動学は、 (i) 対数螺旋を仮定。ピッチ角は固定。 (ii) ストリーミング速度はサイン関数。銀河中心に対して 　　　　VR = -ARcos(χ(R,θ)) 　　　　VT = Aθsin(χ(R,θ)) ここに、χ(R,θ) = mΘ - Φ(R) ＝腕重力ポテンシャルの位相。 m = 腕の本数、Φ(R) ＝動径位相関数。 モデルデータの作成は Simonson (1976) に倣った。彼は二本腕を仮定したが、 この論文では、腕が事前に選んだ６か所を通過することを強制し、腕本数と ピッチ角はフリーパラメタ―にしたところが異なる。速度振幅は、 AR = Aθ = 8 km/s を仮定した。腕と腕間での 密度比は 3 : 1 とした。 　A. ４本腕の基礎　 　最初は２本腕モデルをあつかったが、６か所を通るモデルは作れなかった。 ピッチ角を倍にして、４本腕モデルを使えば６か所を通るようにできる。 パラメタ―を調整していきベストフィットとして、ピッチ角 13° の ４本腕モデルを得た。 　密度波の形成は共鳴領域で制限されるので、４本腕モードは２本腕に 比べ狭い領域に存在する。Lin et al 1969 によると、 (a) もしシュミット回転曲線を採用し、 (b) 渦状構造が内側リンドブラッド共鳴半径と共回転半径の間に存在、 とするなら、４本腕の存在領域は非常に狭くなる。この問題に対応 するため以下のモデルを考えた。 　B. モデル I. 腕なし　 　腕なし　 　 Burton (1971) は HI ラインプロファイルの特徴の幾つかは、ストリーミングに 頼らずに生み出せることを示した。それらは水素の空間分布と、 視線に沿った速度効果から出現するのである。例えば、図２の l = [70, 80] V = 5 km/s の強いピークは視線効果であり、ストリーミングとは関係ない。 真の効果と見かけの効果を区別するため、モデル I では、腕なしとした。

図４．モデル　I の l-v 図。腕無し。見える構造は接点効果による 稜線のみである。 　HI の存在域　 　以降のでモデルでは HI の存在域を R = [4, 16] kpc に限る。そこでの 密度は n(R) ∝ (0.21R3-0.81R2+9.0R-22.5) と表す。この場合、極大密度は R = 8.2 kpc に現れる。R < 4 kpc に対応して、l < 23° は扱わない。 　V から n(HI) へ　 　Δr = 10 pc で視線方向の距離を区切り、通常のシュミット回転曲線 を用いて距離 r から視線速度 V へと変換した。得られた視線方向の速度 プロファイルを半値幅 8 km/s の三角関数で平滑化する。最後に柱密度を 光学的深さに直す。 　モデル I の特徴　 　図４にモデル I の結果を示す。l = [70, 80] の接点効果による強い ピーク以外に目立った特徴はない。したがって、以降現れる構造は全て、 腕に付随すると考える。

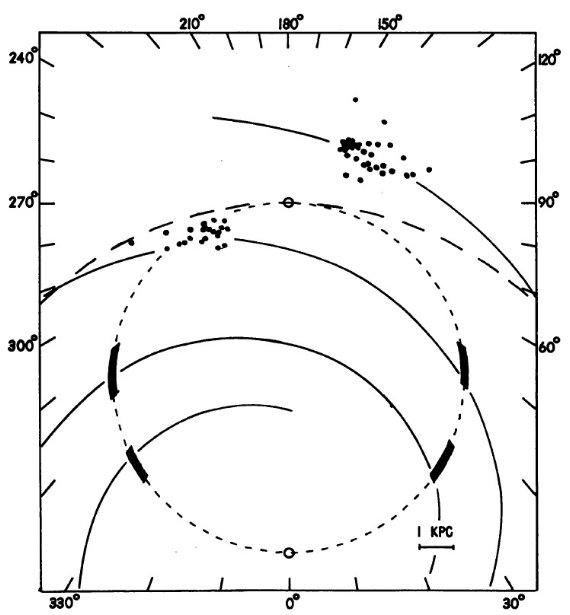
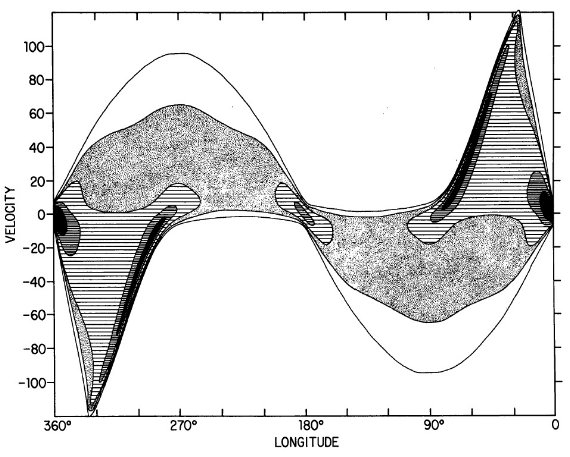
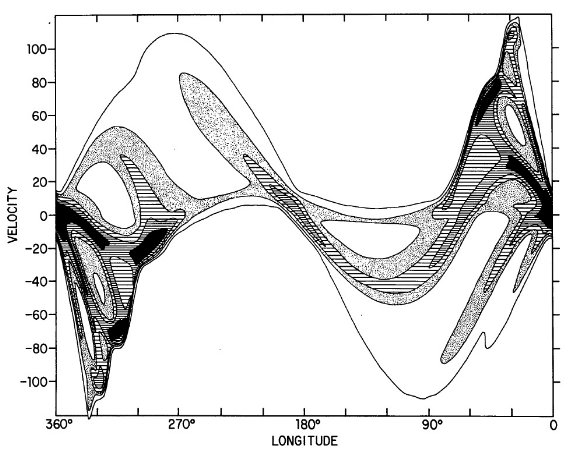
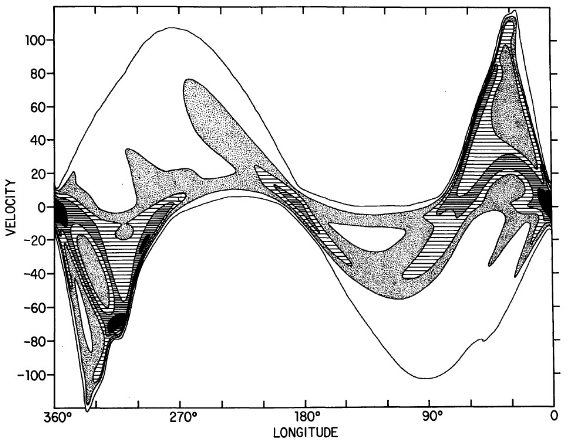
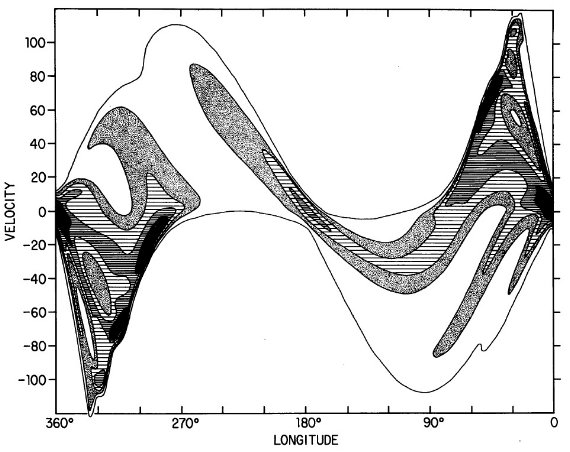
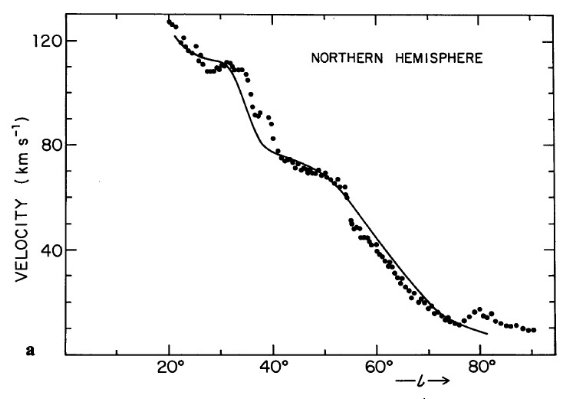
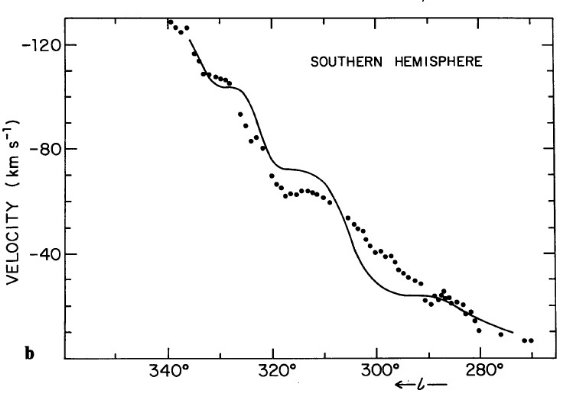
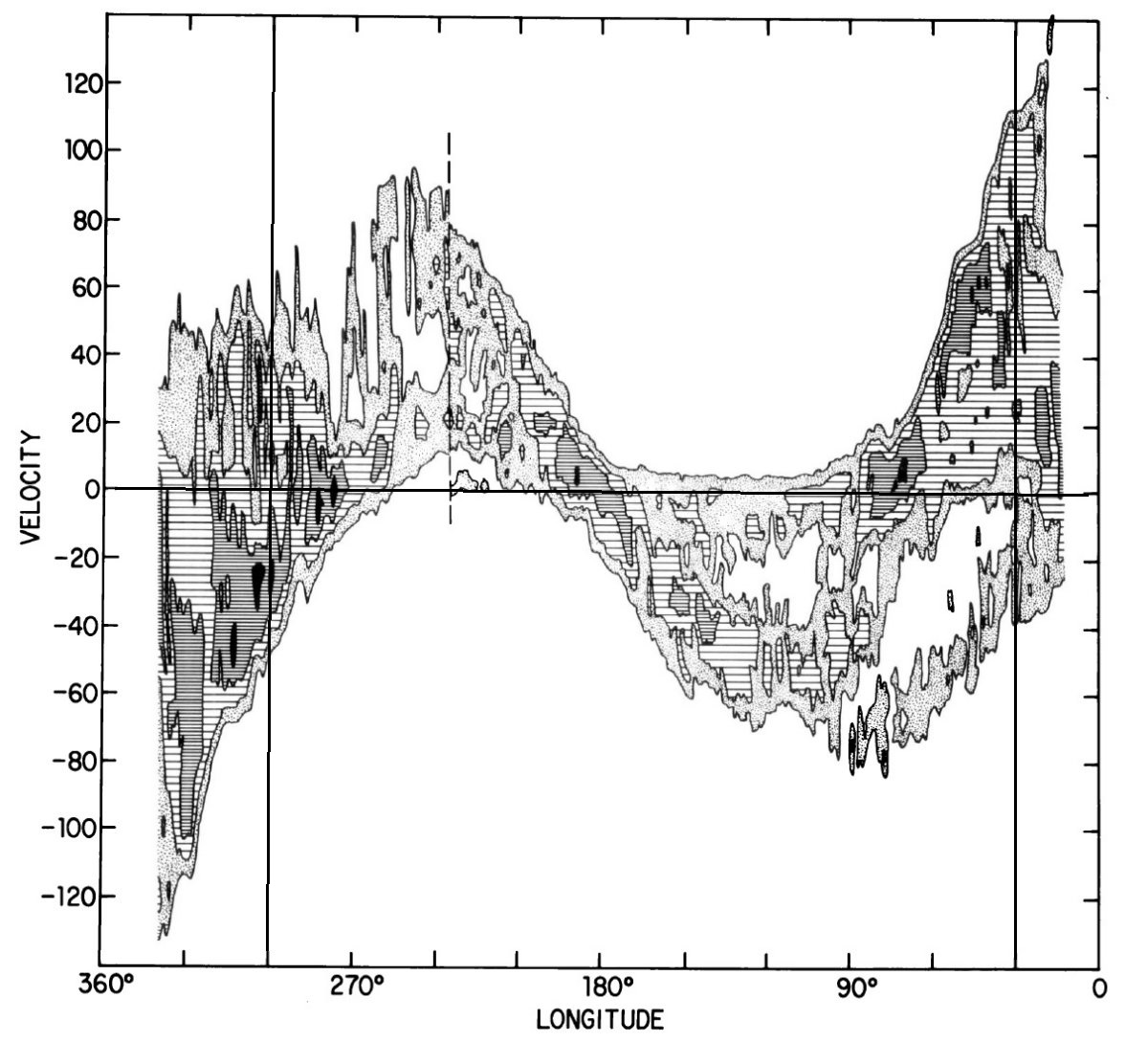
図５．モデル II = ４本対数螺旋腕。図２の全体パターンを再現する。 R > 10 kpc 、つまり V ≤ 0 (l = [0,180]), V &l\ge; 0 (l = [180,360]) での一致に注目。 R < 10 kpc では それほど良く合わない。 　C. モデル II. ４本対数螺旋腕　 　フィットパラメタ―　 　４本腕、ピッチ角 13°、太陽領域の位相 160°、ストリーミング 振幅 7 km/s のモデルが一番良く合う。最終的に決まった接点速度 VT の銀経変化は図３に示した。シュミット回転曲線を使ったので、北銀河の方が 南銀河より観測に良く合う。それにも拘らず、図３で電波４接点の銀経はよく 再現されている。ただし、可視データから決めた l = 290 の辺りは一致が悪い。 　カリーナループ　 　図５にモデル l-v 図を示す。図中カリーナ腕は l = 300° で V = 200 km/s まで伸びるループを形成する。このループは図２（観測）にもはっきり 見える。したがって、図３の接点速度データはこの構造を隠しているが、図２ に構造が現れたということである。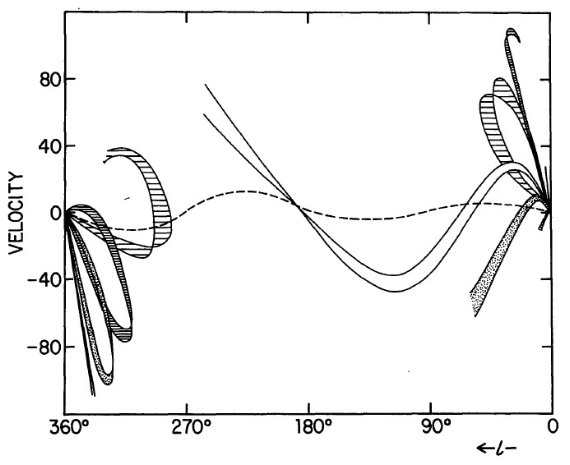 　図６で理解せよ　 　外側銀河系、つまり V ≤ 0 (l = [0,180]), V &l\ge; 0 (l = [180,360]) では４本腕モデルは観測を良く再現している。その理解を助ける目的で図６を 作った。カリーナ腕が作る l = 300 付近のループと l = 240 - 270 で 何の構造も見えないことに注意して欲しい。

図６．モデル II l-v 図の解説図。この図は Weaver et al (1969) が 広めた手法で腕の位置を追跡 　カリーナ腕の対応腕が l = 20 　 　カリーナループは図２にはっきり見える。これは、腕が太陽周円を l = 290 で交差していることを示す。簡単な幾何学から、銀河系の向こう側 l = 20 でカリーナ腕と対称な腕が太陽周円と交差する。これも図２に見える。 データには l = 65 から発生する別の腕が見える。 (どれのことか分からない。 ) 外側銀河系では２本腕が成り立たないことは明らかである。図５に示すように 他の構造も４本腕と合う。面白いのは、主に内側銀河系の観測特徴を説明する ために導入した４本腕モデルが却って外側銀河系を上手く説明している。 　モデル II の失敗　 　内側銀河系はそれほどはっきりしない。実際二つの領域が再現されていない。 (a) l = 70 の構造。モデル I には見えていた。モデル II ではストリーミン グが消し去っている。 (b) l = 300, V = -25 km/s の非常に強いピークも図５にはない。 　局所リング？　 　図２には l = [90, 180] での V = -10 km/s, l = [180, 270] で V = 20 km/s の尾根が見える。我々はこれは近傍水素の判断した。なぜならこの 極大は b = 30° を越えても見えるからである。Burton, Bania 1974 は 銀河円盤の上下に見える特徴が局所ストリームで説明できることを示した。 しかし、我々は円盤内の構造を扱っており、太陽が大きな水素密度の中に いることを要求する。我々は半径 300 pc, 厚さ 100 pc のリング内に 太陽が存在するとした。

図７．モデル III = ２本腕 + 弱い４本腕。４本の内２本は二本腕 に重なる。このモデルは観測の図２に対し、モデル II ほどよくフィット しない。特に R > 10 kpc でそうである。 　D. モデル III. 非対称４本対数螺旋腕　　 　モデル III は二本の強い腕＋２本の弱い腕である。図３a, b を見ると、 l = 30 のストリーミングは l = 330 のより強く、また l = 310 の ストリーミングは l = 50 より 強い。これが非対称腕の正当性の根拠である。 この現象をストリーミング速度を以下のようにして表現する。 　　　VR = -A cos(χ) - B cos(2χ) 　　　VT = A sin(χ) + B cos(2χ) モデル III では A = B とした。密度変化はストリーミングに追随して 変化する。モデル II での密度は (2 + cosχ)の形で変化したので 密度の変動は 3 : 1 になった。モデル III では密度変化は [2+(1/2)(cosχ+cos2χ)] なので、強い腕では密度比 3 : 1 だが、弱い腕＝サジタリウス・カリーナ腕では僅かな変動しか得られない。 A = B の仮定は、４本腕モードをかなり保存することになるが、それでも 外部銀河系における等高線はモデル II に比べると不鮮明になる。 モデル II で問題となった l = 70, 300 の領域はやや改善された。しかし、 全体としては、モデル II の方がましに見える。しかし、この判断は 外側のフィットに重みが掛かっている。内側銀河系で二本腕が卓越し、 外側に行くにつれ４本腕モードに移行する可能性もある。

図８．モデル IV = ４本腕。共回転半径＝ 9 kpc. 多くの点で、 図５と似る。違いは (a) V = 0 km/s 付近でストリーミング運動が消える。 外側銀河で構造が少しずれる。 　E. モデル IV. 共回転半径が内側　　 　ここまでのモデルはパターン速度がガス回転速度より小さいと仮定していた。 そこでは、共回転が起きるのは、水素が観測できる境界の外側になる。 以前に、４本腕モードの範囲は狭いと述べた。したがって、もしそのような モードを存在させるためには、共回転は外側の縁より十分内側になければ ならない。 (ここんとこ不明 ) 　Lin, Yuan, Shu (1969) はシュミット回転曲線を用いると、４本腕モード の存在域が破壊的に小さくなることを示した。データを満足させる別の回転 曲線が可能でなければならないし、実際そうである。 (a) 内側のシュミット曲線は北銀河データに基づいている。南銀河データにも 合うように曲線を下げると、４本腕モードの許容域が内側に伸びる。 (b) シュミット曲線は、速度 Θ = ωR が単調に減少すると 仮定している。しかし、 M 31 では距離大で速度は殆ど変らない。 我々の銀河系でも、 R > 11.5 kpc で回転速度がシュミット曲線より 大きいことが Humphreys 1970 (超巨星)や Balona, Feast 1974 (OB 星), Georgelin 1975 （HIIRs）により示されている。 　それでも許容範囲は狭い。もし、R = 4 kpc を内側共鳴半径とすると、 ４本腕モードの共回転半径は多分 R = 8 - 12 kpc 程度である。この理由で モデル IV でも共回転半径をその範囲内の 9 kpc にした。 その内側では、 AR, Aθ は前と同じである。 それらは共回転半径でゼロになり、その先では符号を変える。 それを表現するのに振幅がサイン関数的に変化し、 R = 9 kpc で AR が符号を変え、Aθ は同じ符号になるようにした。 ただし、シュミット曲線はそのままとする。 その結果、図８を得た。モデル IV は外側銀河系でモデル II と差が出るが、 内側銀河系では l = 70, 300 でモデル I と似る。これはストリーミングが 弱くなったからである。

　３．結論