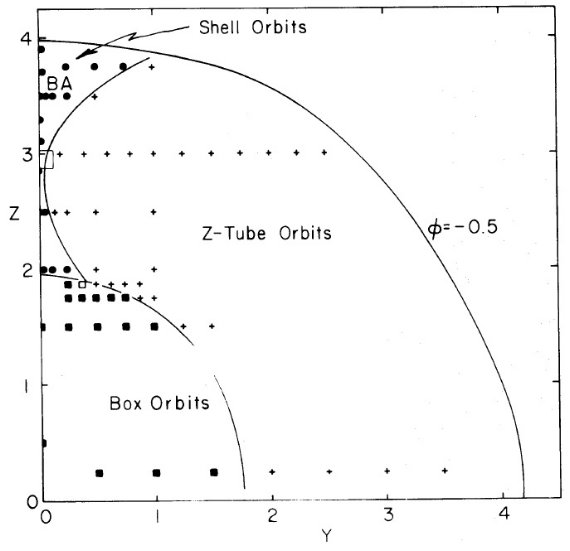
図1.E = -0.5 に対する (Y, Z) 出発平面。各シンボルは軌道の出発点を表す。 十字=Z-チューブ軌道。四角=ボックス軌道。点=シェル軌道。Z = 3 近くの 小さな区画は図2で拡大される。
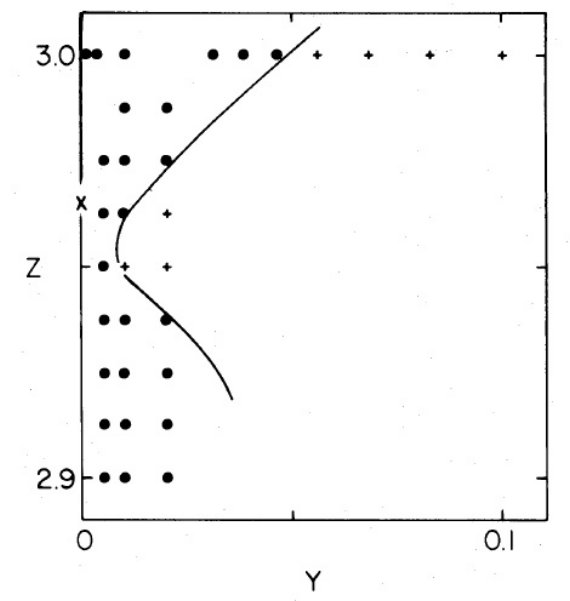
図2.E = -0.5 に対する (Y, Z) 出発平面の一部を拡大。各シンボルは 図1と同じ意味。軌道の出発点を表す。 バツ=(X, Z) 面上の共鳴閉軌道の(Y, Z)出発点。
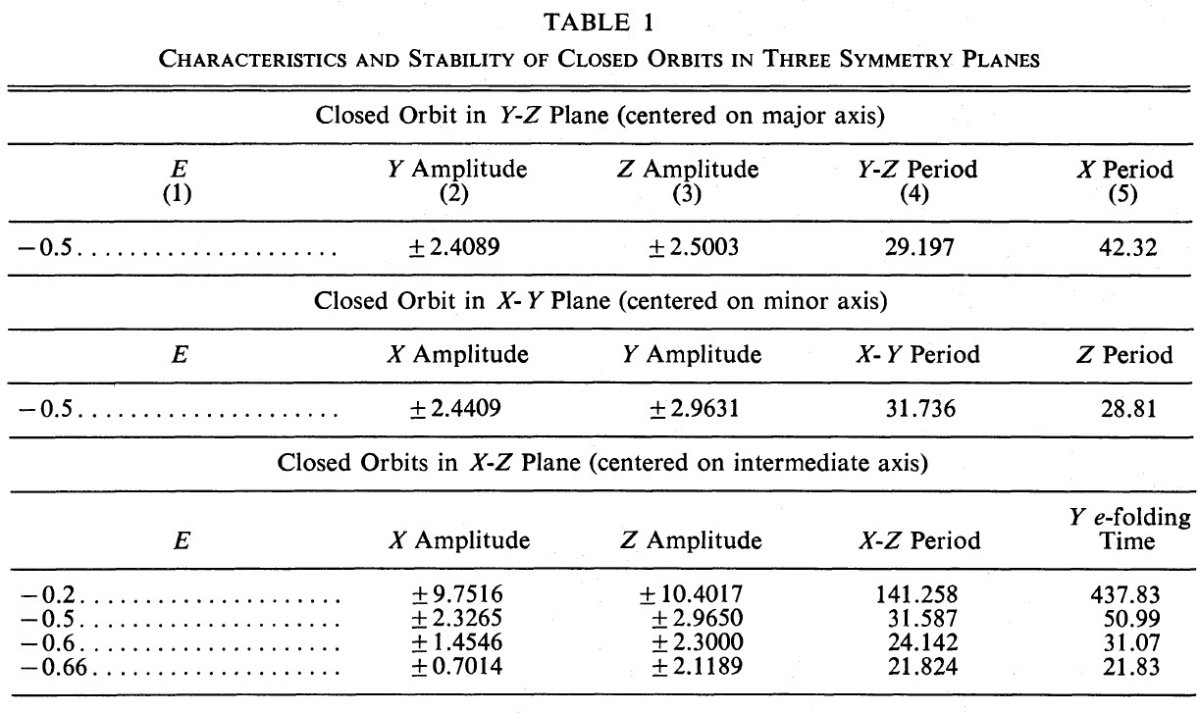
| 前論文では三軸不等モデル銀河の一つを数値的な方法で調べた。最長軸(X) を回るチューブ軌道と最短軸(Z)を巡るチューブ軌道が発見されたが、中間軸 (Y)を巡るチューブ軌道は見つからなかった。 | 今回やはり数値的手段で、調べたモデルにはほぼ確実に Y-軸を回るチューブ 軌道は存在しないことを示した。その代りに新しいシェル軌道族が見つかった。 X-, Z- チューブ軌道の存在と、 Y-チューブ軌道がシェル軌道で交換されることは 三つの対称平面上での2次元共鳴閉軌道の安定性と不安定性を数値的に決定する ことから理解された。 |
|
|
|
 図1.E = -0.5 に対する (Y, Z) 出発平面。各シンボルは軌道の出発点を表す。 十字=Z-チューブ軌道。四角=ボックス軌道。点=シェル軌道。Z = 3 近くの 小さな区画は図2で拡大される。 |
 図2.E = -0.5 に対する (Y, Z) 出発平面の一部を拡大。各シンボルは 図1と同じ意味。軌道の出発点を表す。 バツ=(X, Z) 面上の共鳴閉軌道の(Y, Z)出発点。 |
|
|
|
|
|
|
|
|
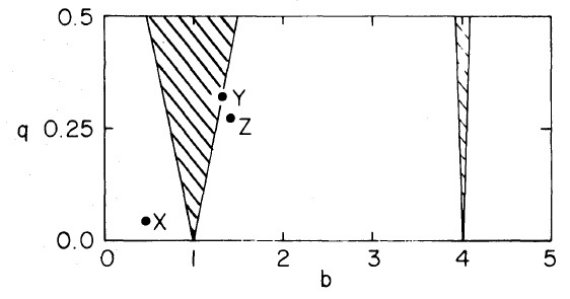 図3.影部=Mathieu 方程式の解の不安定領域。 X, Y, Z の3点はここで 調べた3つの共鳴閉軌道を示す。 |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
