レッドクランプ Ks 絶対等級
Grocholski, Sarajedini (2002)
は銀河系 14 散開星団の 2MASS JKs データと各星団の年齢、メタル量、
ターンオフ距離を用いて、レッドクランプ Ks 絶対等級
MKsRCを年齢とメタル量の関数として定めた。彼らの
研究によると、若い RC (t ≤ 3 Gyr) では MKsRC
に 1 mag に達する変動がある。従って RC を標準光源として使おうとする時
には年齢とメタル量の知識が必要である。
LMC 距離と Ho
Ho を決める HST キープロジェクトは LMC 距離に (m-M)o = 18.5±0.1
(madore, Freedman 1991) を採用して、LMC セファイドの PLR を定めた。
Freedman et al 2001 はこの関係を利用して多数の銀河距離を求めた。それらは
タイプ Ia 超新星その他の第2標準光源の較正に用いられた。
| |
Ho = 72±8
km/s/Mpc の 9 % エラー中、6.5 % は LMC 距離のエラーが原因である。
しかし、彼らが採用した距離は文献中の距離の平均値であり、その基礎となる
個々の値は互いに大きく矛盾している。一般に LMC 距離は「大きな距離」18.5
- 18.7 mag と「小さな距離」18.3 mag に分かれる。「大きな距離」は主に
種族I天体、「小さな距離」は RR Lyr から求められている。Clementini et al
2003 は距離決定手法を詳細に検討し、「大きな距離」と「小さな距離」は測光
の精度と赤化補正の改良で収束可能であるとした。彼は平均値として、
(m-M)o = 18.515±0.085 としたが、この値は Freedman et al 2001 の
18.5 と一致する。
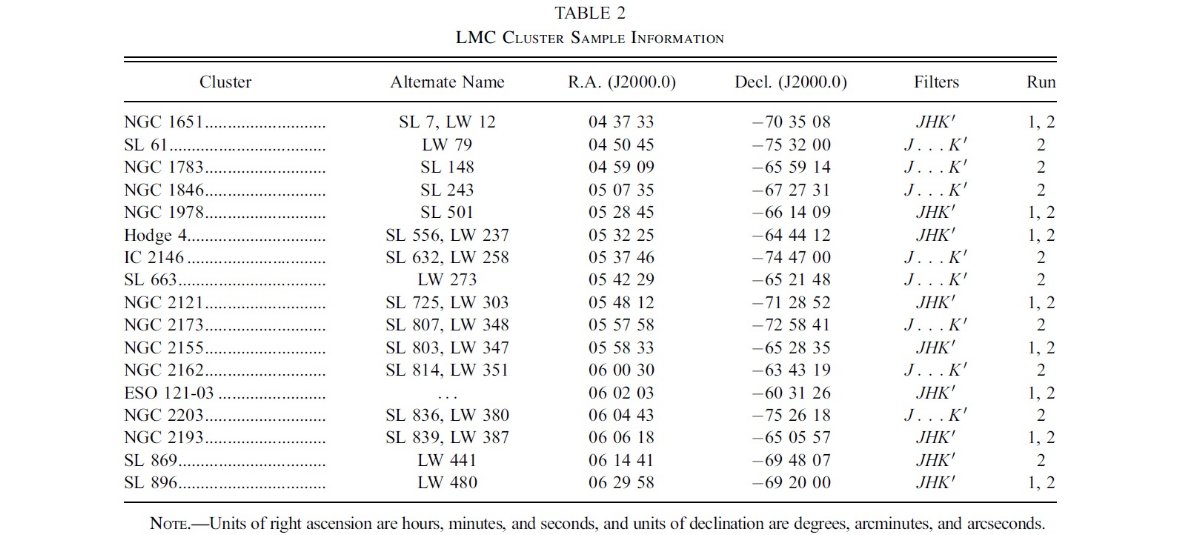
星団距離
LMC 星団システムの空間分布を求めるために、
Grocholski, Sarajedini (2002)
の手法を用いて 17 星団の距離を決定する。さらにそれらから LMC 中心までの
距離を決定する。
|