アブストラクト銀河系楕円体の最近の結果を解析し、非常に平坦な成分の存在を確認した。 この成分は太陽近傍で 2 % を占める。しかし、高速度星とは一致しない。そ れらの星は軸比 1;4 の楕円体か、スケール高 1.5 kpc の | 指数関数円盤としてか の形で分布する。 z = 1.5 kpc で密度分布が急変することで測光的には銀河系 古い円盤、スケール高= 300 pc とは、明確に区別される。この種族は従って、 円盤ではなく楕円体種族である。しかしその運動学的特性は高速度星のそれとは 違う。系外銀河の内側楕円体は運動学的にはスムーズに楕円体から円盤へと移行 する。そのモデルはスターカウントデータとよく合う。 |
|
銀河系の二成分モデル 良く議論される銀河系モデルは薄いはっきりした回転円盤が大きな非回転球形成分 に埋まっているという姿を描いている。円盤は近似的にはスケール長 3.5 kpc、 スケール高 0.3 kpc の二重指数関数形を持つ。回転速度 V は速度分散 σ に較 べると大きく、V/ σ ∼ 4 である。円盤のて典型的メタル量は太陽の ファクター数分の1以内に収まる。楕円体成分は回転速度が小さく、速度分散が大きい。 メタル量は低く [Fe/H] ∼ -1.5 である。このモデルには中間種族は存在しない。 このタイプのモデルは Bahcall,Soneira 1980 により広範に調べられた。 第3成分の存在 星計数データ解析からは全く異なる結論が導かれた。Becker 1980, Brooks 1979, 1981, Chiu 1980 , Gilmore,Reid 1983 は全て楕円体が著しく平坦であることを示した。 その上、Brooks, Chiu, Gilmoire/Reid は内部楕円体の星のかなりが空間分布も運動 学的性質も円盤と外側楕円体の中間の成分に属する証拠を上げた。系外銀河の測光 及び運動学観測は類似の成分を見出している。 |
Bahcall, Soneira モデルのパラメターからの結論 Bahcall, Soneira モデルのパラメターからは次の結論が導かれる。 (1)最近の星計数は誤っている。(第2章) (2)銀河系は他の銀河と似ていない。(第3章) (3)中間運動種族の、z 運動と z 密度分布に関連が無い。(第4章) 両モデルの比較 我々は「厚い円盤」を含むモデルを提示する。星計数データの解釈では二成分モデル も厚い円盤モデルも同じようによいフィットを示し、星計数のみでどちらが正しいかは 決められないことを示す。化学組成や運動学的特性と星計数データを結合し、系外銀河 の観測と合わせて解釈した時に「厚い円盤」モデルがより良いことが判る。 |
Gilmore,Reid 1983
で、内部楕円体は軸比 1 : 4 の扁平な形で、太陽近傍星の 2 % がそれに
属すると結論した。我々は他の著者による研究もそれと一致することを注意した。
一方、 Bahcall, Schmidt, Soneira 1983 はそれらのデータを再解析して、平坦な
成分は存在せず、軸比は 1 : 1.2 以上にはなり得ず、規格値も 0.1 % と小さい
と主張した。この矛盾を解くため、最近の結果を調べる。
2.1.バーゼル測光サーベイこの測光は GRU システムで測光視差を決めている。紫外超過パラメターが統計 的なハローと円盤の分離に用いられ、|b| > 10° 8領域の密度則が導かれた。 銀極方向は Frankart 1969, Frankart,Schaltenbrand 1977 が調べた。ハロー 密度分布は 1 < z < 5 kpc の範囲でスケール高 0.5 kpc の指数関数で 表現される。しかし、 Bahcall, Schmidt, Soneira 1983 が指摘したように、スケ ール高がこんなに小さいことは円盤成分の混入がハロー成分にあったことを 示唆する。彼らの密度則を詳細に調べると、明るく遠い 4 < MG < 5 の分布は他の星より平坦な分布を持つことが判る。そのスケール高は 1 kpc である。密度則を調べると、この等級の星への円盤からの混入は z > 1 kpc で10 % 以下である。スケール高は 0 < z < 4 kpc では 1kpc, 5kpc < z < 8 kpc では 8 kpc である。この密度則が楕円体成分を表わしていると考えると、 5 < z < 8 kpc で決めた密度則を内側に延長すると、z < 5 kpc では かなりの密度超過が存在することになる。2.2.ストレームグレン測光サーベイ極端種族II と 中間所属II の F 型星ストレームグレンは高銀緯 F 型星の観測を進めている。最近の予備的結果は Crawford,Mavridis, Stromgren 1979 を見よ。このサーベイは星を極端種族 II , δ(u-b)0.6 > 0.16; [Fe/H] < -0.75, と 中間種族 II 0.16 > δ(u-b)0.6 > 0.08; -0.75 < [Fe/H] < -0.4 に分類する。この定義によると、太陽近傍では中間種族IIは古い円盤の 6 %、 極端種族IIは (6.6±2.6) 10-2 を占めている。北銀極方向の テストサーベイによると、z = 1 kpc の高さでこの数字は中間種族 II で 1/3, 極端種族II で 1/100 に低下する。その結果、そこでは、つまり Mv = 4.5 - 5.5 の 星に対して V = 14 - 16 の領域で、二つの種族の密度は同じくらいになる。 二つの種族の密度低下量 中間種族II がそのメタル量から予想されるように古い円盤種族の矮星であると 考えれば、その密度低下が急であることは容易に理解できる。極端種族 I の星の 場合、 z = 1 kpc で密度が 1/3 になったことはスケール高 1 kpc に対応する。 この低下量はドボークルー則に従った場合の 1/1.4 より遥かに急である。 極端種族II のスケール高 以上の結果から、適度に低メタルから極端に低メタルの星に至る種族は z = 1 kpc までの密度低下を見るとスケール高 1 kpc の分布則を持っているようだ。 |
2.3.バークレイ運動学及び測光サーベイ2 成分では不十分Chiu 1980a は 3 領域、合計 0.6 deg2 での運動学・測光サーベイを V = 20 まで実施した。その結果、円盤と楕円体に対して光度関数を導き、空間 密度と運動学的密度を求めた。彼の解析によると、単純な 2 成分モデルではデータ を上手く説明できない。そこで、彼は二つの修正モデルを調べた。第1モデルは 軸比 1:3 - 1:4 の扁平楕円の追加で、第2モデルでは球形の楕円体を保持し、 軸比 1:3 - 1:4、運動特性が円盤と楕円体の中間の中間成分を加えた。Chiu のデータ からは、はっきり分離した中間種族が存在するか、円盤から楕円体へ運動特性が 滑らかに移行しているのかはっきりしない。しかし、いずれにせよどちらも含まな いモデルは否定される。 Brooks の解析 Brooks 1981 は Chiu のデータを解析し、楕円体のパラメターとして以下の組み 合わせが許されることを見出した。 1:3 R-3 3.5 % 1:4 R-3 0.6 % 彼女は古典的な楕円体パラメター、1:2 と 0.12 % ( Schmidt 1975, Bahcall,Schmidt, Soneira 1983) が観測結果と合うためには上述の第3成分が存在する場合のみである ことを示した。 2.4.深い測光サーベイパラメターを一意に決めるのは困難12 の各領域 0.4 deg Kron 1980 の星計数データ Bahcall,Soneira 1981 は Kron 1980 の星計数データを二成分モデルで解析した。 彼らは規格値 0.125 % が合うことを見出した。ただし軸比は 1:1.1 となった。 Bahcall, Schmidt,Soneira 1983 はスケール高 1 - 2 kpc の中間種族の上限として 円盤密度の 1 - 15 % とした。 等級で z 範囲が変わる 浅い測光サーベイが平坦な中間種族の存在を与え、深い測光がその上限を与える だけなのはそれぞれが探る典型的深さの差によるものとして理解できる。深い測光は 高銀緯の狭い領域に限られ、解の重みは V = 20 - 22 に集中する。これらの星は Mv ∼ +5 で z = 10 - 20 kpc の楕円体準矮星か、Mv ∼ +12 で z < 1 kpc の円盤赤色矮星である。z = 1 - 5 kpc 領域の星は十分には採取されない。この 領域の星は V = 15 - 20 でよく採取される。 |
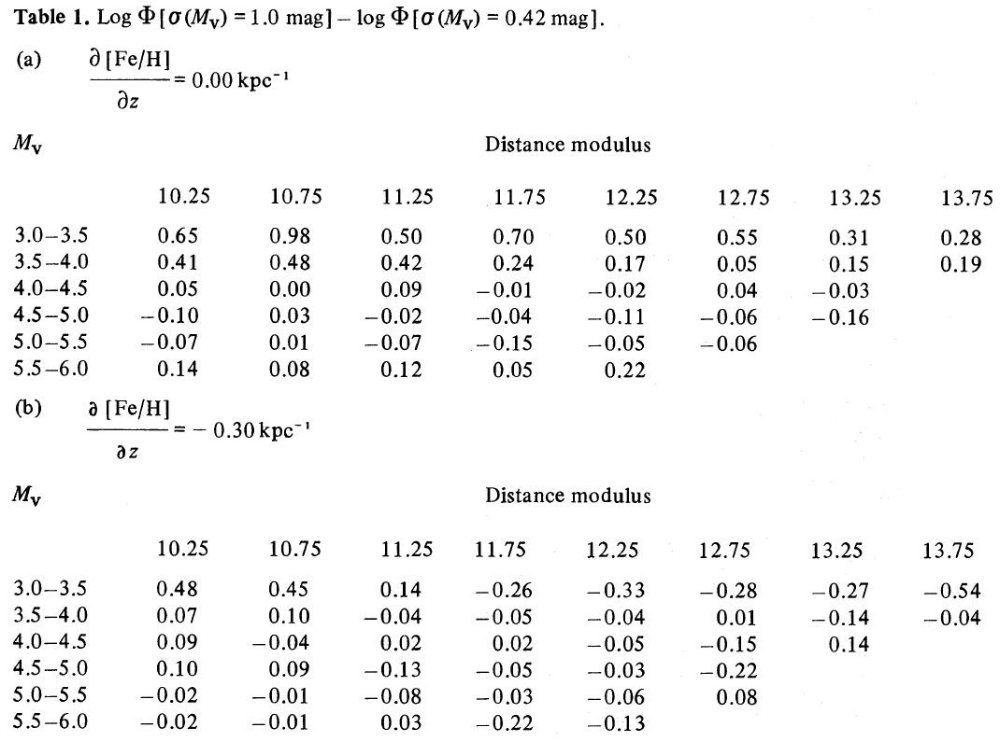
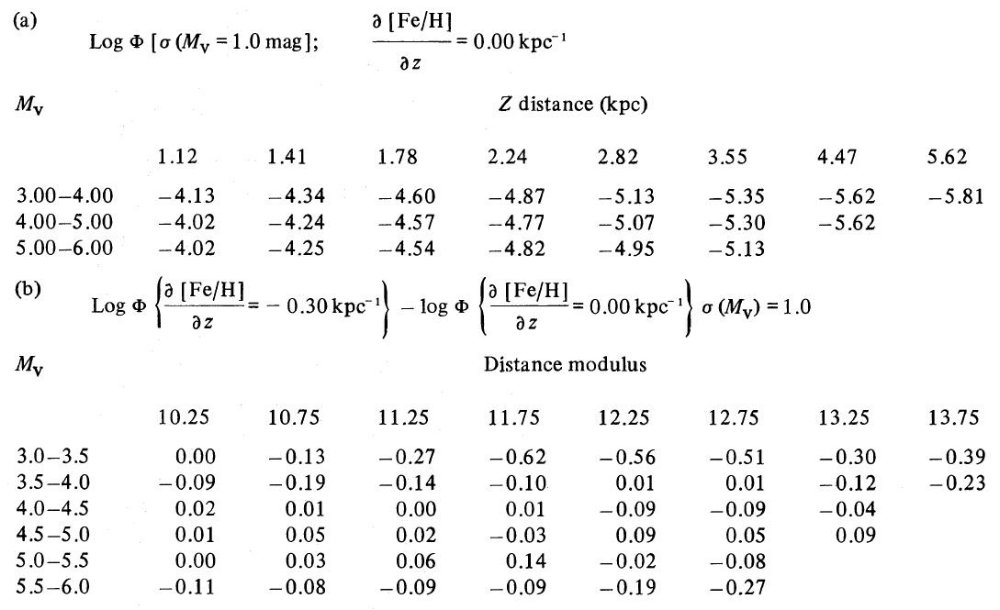
2.5.UK シュミット測光サーベイBahcall の批判Reid,Gilmore 1982b と Gilmore, Reid 1983 は中深度 V = 15 - 20 での広範な探査である。その結果、以前の研究で 存在するのではないかと疑われていた中間種族が軸比 1:4 の楕円体でも スケール高 1.5 kpc の円盤でも同じようにうまく表現されることが明らかに された。この種族は Bahcall et al 1983 により、不適切な絶対等級ーカラー 関係を使用したための虚構の産物とされた。 Gilmore, Reid 1983 の結果は他の研究結果とよく合っているので、もしこの批判が正しければ、それら の研究も誤りということになる。したがって、この矛盾の起源をはっきり させることは非常に重要である。 批判への反論 通常エラーの原因となる、測光較正と赤化の扱いは今回は問題にならない。メタル量 分散と光度クラスの問題は相互に関連し、適切なる等級・カラー関係の選択と 等値である。低メタル主系列星は太陽メタル主系列の下に並ぶ。この効果を取り入れ るため、 Gilmore, Reid 1983 では、(1)z = 0 - 5 kpc で ∂[Fe/H]/∂z = -0.30 kpc-1, その先平坦という場合と、(2)メタル勾配なし、の二つの場合を考えた。メタル勾配 を考えた(1)では z ≈ 5 kpc では同じカラーに対し Mv で 0.85 mag. 暗い ことになる。(2)のゼロ勾配は物理的には低メタル種族星がゼロ年主系列から 0.85 mag. 離れた進化効果と同等であり、その理由で考慮されたのである。だから、これは 全ての星が進化していないという仮定とは異なる。導かれた星密度は 0.6 ≤ B-V ≤ 0.8 のカラーに対しては以上の仮説に影響されにくいことが判った。これは我々が 採用した色・等級関係と、K 型星を考察から除いた事が適切な結果に導くことを 保証する。 ターンオフ付近 可能な批判として、ターンオフカラー B - V ∼ 0.4 付近の星に対しては Mv で 1.5 mag の巾が測光不定性として対応するというものである。平均 Mv で 0.85 mag のズレが適切としてもその値の周りで分散が 1 mag となる。準巨星に対し計算した マルムキスト補正の値は大きなまちがいとなる。そこで、我々はメタル勾配=ゼロ、 分散= 1 mag を仮定してマルムキスト補正を再計算した。この仮定は物理的には ターンオフカラーを持つ全ての星が ZAMS から 0.85 等上がった準巨星であると することに等しい。この値は平均距離準巨星が球状星団色等級図のターンオフカラー での主系列の上にいることと一致している。この再計算の効果は表1と表2に載せた。 全ての星が準巨星という仮定と全ての星が矮星という仮定との差は 4.0 < Mv < 6.0 で 15 % 以下である。この等級帯は Gilmore,Reid 1983 が使った箇所 である。この効果はもっと明るい星ではより大きくなり、Mv = +3.5 付近の光度 関数の形に影響を及ぼす。 |
準巨星の扱い方 B - V = 0.6 付近の星に対して導かれたパラメターの信頼性は Trefzger, Pet, Blaauw 1983 の仕事からも支持される。彼らは Walraven 測光を南銀極方向 1 deg 2 内の V ≤ 14.5 の F, G 型星に対して行った。全ての星の表面 重力はそれらが未進化の主系列矮星であることを実証した。Mv > +6 の主系列星 が混同されるのは Mv < +2 の真の巨星とである。この光度の巨星は分光的に 矮星から区別され、それらの表面密度には制限がある。 Chiu 1980 は完全サンプルの 光度クラスを決定しようと試み、 楕円体星 15 < V < 17 の 30 % は進化した 準巨星、巨星であるとした。17 < V では巨星の割合は無視できる。 同様の結果は Weistrop 1972 の銀河モデルでも得られた。 Ratnatunga 1982 は現在 (l、b) =(270°, -45°) 20 deg2 内、13.5 ≤ V ≤ 16.25, B - V ≥ 1.0 の巨星を探すサーベイを行い、1.0 ≤ B - V ≤ 1.2、13.5 ≤ V ≤ 15.0 では 24 % が 47 Tuc 的な巨星、15 % が M 92 的な 巨星、60 % が矮星という結果を得た。15.0 ≤ V ≤ 16.25 ではその数字が 13, 2, 85 % となる。これらの結果は、z = 10 kpc 地点では [Fe/H] ≈ -0.75 の星が -2.0 の星より多いことと、V ≤ 15 では進化した星の割合が 少ない(∼ 40 % )ことを示す。 読み違いでなければ 40 % を "significant minority " と呼んでいる 巨星を見落としていたが結果は大丈夫 したがって、星の光度クラスの分類に注意が不十分であったが、 Gilmore, Reid 1983 の結論への影響は大きくなかった。注意しておくが、巨星という言葉を不正確 に使用すると大きな混乱が生じる。赤い巨星は主系列から遠く離れているが、 青い場合(準巨星)は主系列からそんなに離れていない。ターンオフ近くの カラーでは星の絶対等級は主系列星とその1等上との間に分布する。これは 大雑把に言えば主系列の巾の倍程度である。その後、急速に赤い方へ進化し、 光度関数の急落を導く。星が赤色巨星枝に辿りつくとその寿命は再び長く なり、主系列の5−6等上に位置するようになる。真の赤色巨星は 測光距離を使う議論からは外すべきである。いっぽう、ターンオフ付近の 準巨星は上に述べた扱いが適当である。 |

|
銀河バルジの運動 銀河系と似たタイプの銀河のバルジに対する運動学の研究が進み、中心部から 10 kpc までのバルジの運動学が判ってきた。我々の銀河の太陽軌道内のバルジ に関し、Kormendy, Illingworth 1982 や Davis, Illingworth 1983 の系外銀河 の知見を参考にまとめると、 (1)最大回転速度は系全体の速度分散と同程度である。 (2)回転速度は光度 z と共に滑らかに減少する。回転速度にバルジと円盤の 境界を示す特徴は見られない。 (3)バルジ内で速度分散は一定である。 (4)副軸回転はない。 銀河の3成分 Tsikoudi 1979, Burstein 1979, Jensen, Thuan 1982, 特に van der Kruit, Searle 1982 の銀河表面測光によると、円盤に垂直な輝度プロファイルは3成分モデルと 合致する。それらは、 (1)古くて薄い円盤。スケール高 < 500 pc |
(2)41/4 則の楕円体。軸比 ∼ 1:2 ただし、Tsikoudi 1979,
Jensen, Thuan 1982 は指数関数則でも可としている。 (3)厚い円盤。スケール長は薄い円盤と同じ。スケール高は中心からの動径 距離によらない。 カラーと表面輝度の分布から van der Kruit, Searle 1982 は厚い円盤を銀河楕円の 等温成分とし、その平坦化は薄い円盤の重力効果が原因とした。一方、運動学的 研究からは、平坦化には回転と速度分散の非等方性が必要である。 銀河の観測結果 Monet,Richstone,Schecter 1981 は Bahcall, Soneira が仮定した球形の 楕円体は銀河として非常に珍しいと指摘した。Freeman 1983 は M 31 の高メタル 球状星団は回転する平坦な系を、低メタル星団はより広がった回転しない 分布を成すことを見出した。Zinn 1982 は我々の銀河系も類似の2成分球状星団系 を持つことを示した。Kormendy 1982 は測光的に区別されるバルジと円盤が銀河の 輝度分布に良く合うことを示した。 銀河系への類推 銀河との類推から、銀河系の楕円体も測光的に円盤から区別され、適度に平坦で あると考えられる。運動学的には回転速度は高度と共に低下して行く。高速回転の 円盤と回るとしても遅い楕円体との間に鋭い区別は存在しない。 |
|
太陽近傍の中間種族 Mihalas,Binney 1981 Chap7 は太陽近傍の運動特性を色々な年齢と運動学からなる 円盤とそれに楕円体成分として解釈した。彼らのモデルは楕円体内部に中間種族 が存在することや、内側楕円体がかなりの回転速度を持つことを許さない。 しかしかれらのまとめによると、運動学特性は 楕円体: 低メタル RR Lyr ΔS > 5 ⟨θ⟩ - θo ∼ 220 km/s, ⟨Π2⟩1/2 ∼ 210 km/s, ⟨z2⟩1/2 ∼ 90 km/s 中間種族: LPV 150 < P < 200 d, ⟨θ⟩ - θo ∼ -105 km/s, ⟨Π2⟩1/2 ∼ 95 km/s, ⟨z2⟩1/2 ∼ 60 km/s 弱い線の FG 星 ⟨θ⟩ - θo ∼ -120 km/s, σ ∼ 90 km/s G タイプ球状星団 ⟨Π2⟩1/2 ∼ 120 km/s, σ ∼ 100 km/s 低メタル巨星 ⟨z2⟩1/2 ∼ 44 km/s 古い円盤: 高メタル RR Lyr ΔS < 5 ⟨θ⟩ - θo ∼ -50 km/s, ⟨Π 2⟩1/2 ∼ 60 km/s, ⟨z2⟩1/2 ∼ 30 km/s 中間種族と G 型球状星団 Mihalas, Binney は上の中間種族、球状星団は除くが、を全て古い円盤の高速 テールの成分とした。しかし、彼ら自身のまとめにあるように、Wielen 1977 の解析 では巨大分子雲による散乱効果で古い円盤の星が到達する最大分散は、 ⟨θ⟩ - θo ∼ 40 km/s, σ ∼ 80 km/s である。 密度波による散乱も似た程度の値しか与えない。もう一つ注意すると、G 型球状星団 の運動特性が中間種族星と一致しているのが偶然でないとするなら、それらの星は 円盤から散乱されたものではないことになる。球状星団をその高さまで散乱させる 天体は存在しないからである。 低メタル RR Lyr 星 太陽近傍 (d < 3 kpc) の低メタル RR Lyr は非等方性の高い速度分布を示す。 Woolley 1978 によると、R2 : &Phi:2 : θ2 ∼ 3 : 2 : 1 で、この星の系が平坦なのは、回転効果に加え、速度分布が非等方 なためである。 Oort 1965 は 「RR Lyr は真に中間種族であり、ハロー種族と円盤種族の混合物では ない」 と述べた。我々は、さらに ⟨z2⟩1/2 ∼ 50 - 80 km/s で、規格値が約 1 % の種族の存在は銀河系 Kz 則からの一般的な結論であることを 注意する。 |
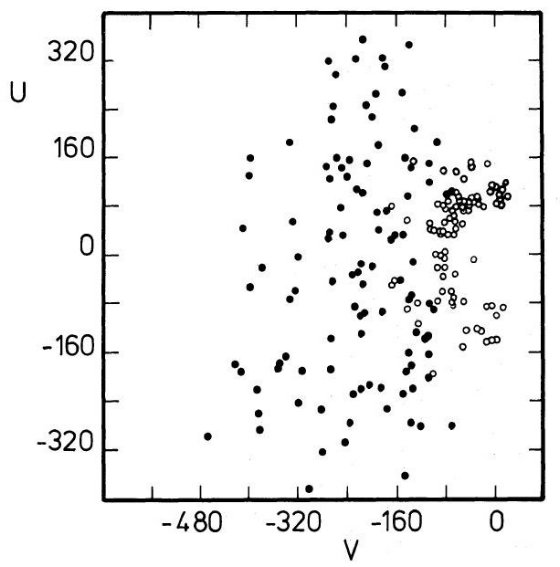 図1.高速度星の UV 分布(Eggen 1964)。白丸=[Fe/H]≥-0.8, 黒点=低メタル星。円盤星は原点付近の空白域を占める。極端準矮星から円盤星への 運動学的性質が連続的につながっていることが判る。 中間種族高速度星の分布 近傍に存在する楕円体成分星の運動学的性質は図1のボットリンガー図に明らかで ある。図には、円盤星と極端準矮星との運動学的な中間位置を適度に低メタルの星が 占めている。これらの星は離心率 e < 0.42 である。より最近、 Eggen 1982 は δ ≤ +30°, V < 15, μ > 0.7 arcsec/yr の完全サンプル 761 星の測光結果を報告した。これらのデータから、楕円体星/円盤星 = 2 % である ことが結論された。この結果は Gilmore, Reid 1983 とよく一致している。この図は Schmidt 1975 による 0.1 % と大きな違いを示して いる。 |
|
星計数だけではパラメターが決まらない これまでの議論で Brooks, Chiu 1980a, と Gilmore, Reid 1983 が各自の星計数から求めた銀河系の構造パラメターが互いに整合し、 銀河の観測とも合致することが示された。それらは Bahcall, Soneira 1981 で与えられたパラメターとは異なる。しかしながら 彼らも星計数データをそのモデルで良く説明されることを示した。 このようなパラドックスの原因は、星計数データのみで銀河系構造を 一意に定めることが出来ないからである。この問題は、 Chiu 1980b, , Brooks 1981, Gilmore 1981, Pritchet 1983 が論じている。そのどれもが強調しているのは 銀河系構造パラメターが相互に合い補い合って、異なるセットが同じ 星計数データを説明することである。したがって、それ以外の要素を考えて 選択する必要がある。 観測とモデルの比較 図2−5では Chiu 1980, Kron 1980 のデータを表3のパラメターでもモデル と比べた。データ数が小さいためカラー区分は広い。それでもカラー分布の 双峰性はモデルで良く表現されている。この点は Bahcall, Schmidt, Soneira 1983 が「厚い円盤」モデルでは双峰性を表現できないとしていたことに 反する。 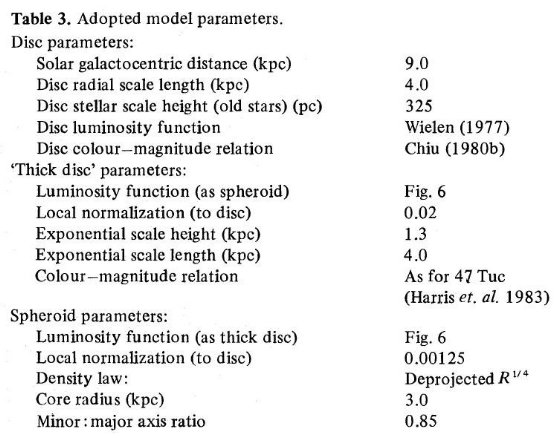 表3.採用したモデルのパラメター |
なぜこのように異なる結論が出てきたかと言うと、モデルの結果が
適用する光度関数の性質に大きく影響されるからである。今回のモデルでは
図6に示す光度関数を用いた。それは基本的には古い円盤種族の光度関数である。
これに対し、 Bahcall, Soneira は若い円盤種族の光度関数を採用し、しかも
それを全ての星種族に適用している。
光度関数依存度が強過ぎる ある点での真の光度関数が何であるかに関係なく、モデルが光度関数に こんなに鋭敏だと、他の構造パラメターを導く事は今のところ困難である。 それはここで示したモデルについても言え、このモデルは単に提案されてきた 色々なモデルが単一に決まらないことを強調するために提出されたので ある。 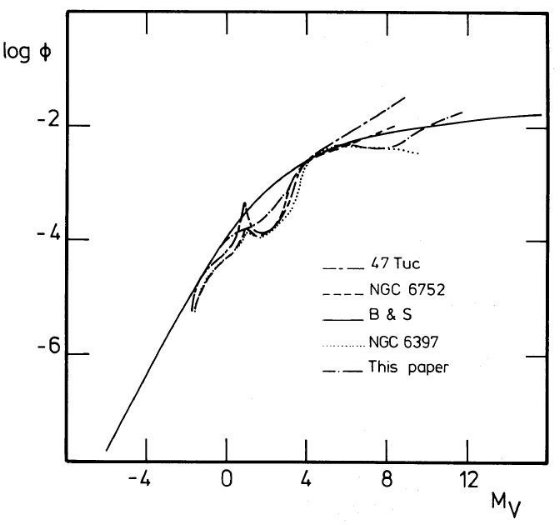 図6.採用した光度関数。他は、Bahcall, Soneira 採用。Da Costa 観測の 球状星団データ。Mv = +4 で規格化してある。 |
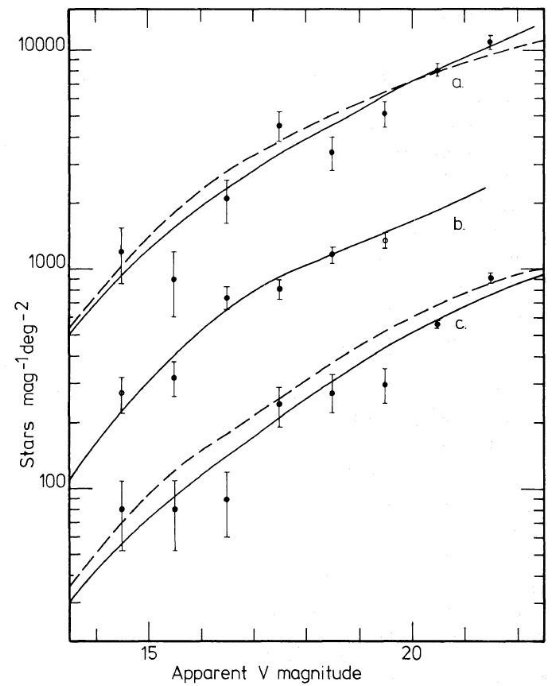 図2.Chiu 1980 V < 20, Kron 1980 V > 20 の星計数。 (a) SA 68 (l,b)=(111,-46) (b) SA 51 (l,b)=(189,21) (c) SA 57 (l,b)=(65,86) 実線は「厚い円盤モデル」、破線は B&S モデル 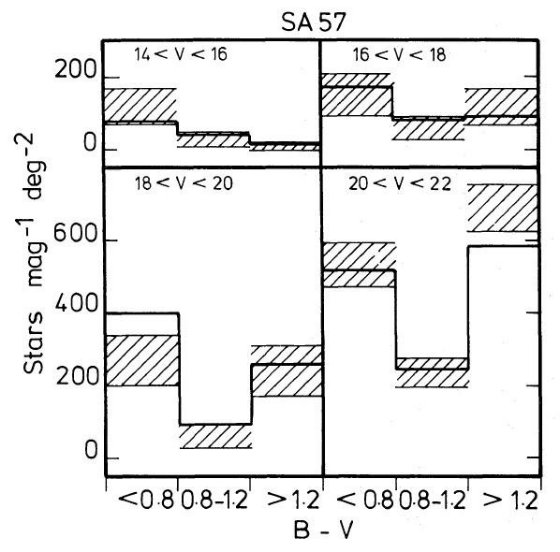 図3.斜線は SA 57 の観測表面密度 ±1σ 値。 Chiu 1980 V < 20, Kron 1980 V > 20 太い実線はモデルフィット。 |
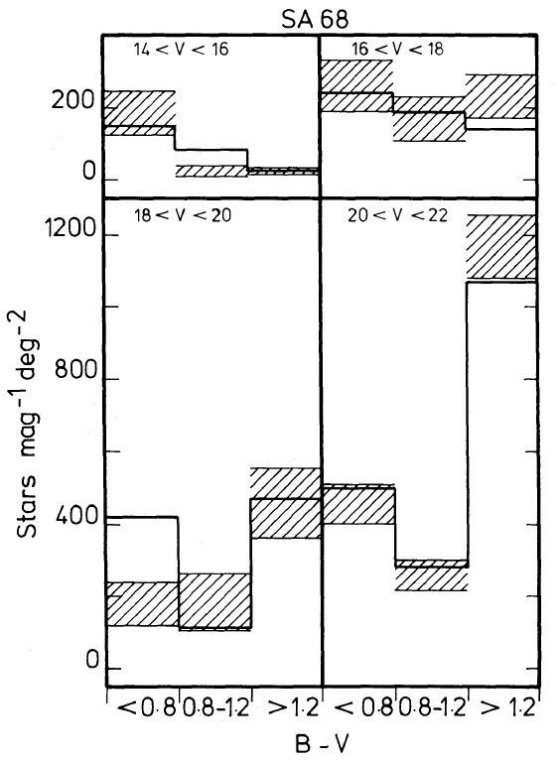 図4.斜線は SA 68 の観測表面密度 ±1σ 値。 Chiu 1980 V < 20, Kron 1980 V > 20 太い実線はモデルフィット。 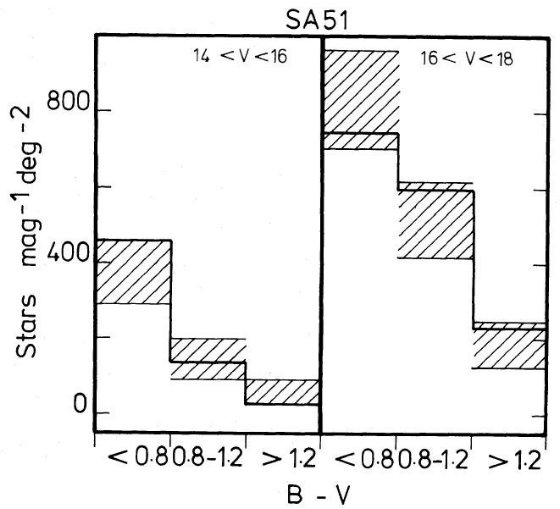 図5.斜線は SA 51 の観測表面密度 ±1σ 値。 Chiu 1980 V < 20. 太い実線はモデルフィット。 |
|
楕円体構造への拘束 これまでの議論から楕円体構造に次のような拘束がかかる。 (1)銀河面近くの楕円体は軸比 1:4 程度に平坦で回転している。 (2)回転速度は銀河面高度と共に滑らかに低下して行く。 (3)銀河中心距離 10 koc より先にメタル量勾配はないか、極めて小さい。 (4)しかし、その内側でメタル勾配はかなり大きい。その原因が単一成分の メタル勾配か、二つのメタル量種族の混じり方か不明である。 (5)楕円体は測光距離で決めた密度勾配でははっきり円盤と区別される。 メタル量もその付近で大きな変化を示す。 二つのモデル この様な観測的拘束に対して、次の二つのモデルが可能である。 (1)単一成分楕円体。内側で組成と運動の勾配がある。 (2)平坦で比較的ゆっくり回転する高メタル楕円体がより広がっていて殆ど 回転しない低メタル楕円体に埋もれている。 |
最近の銀河系形成モデル 主に Jones, Wyse 1986 に従うと、 (1)プロト銀河内はジーンズマス 106 Mo 程度の雲で構成。 (2)雲内で星形成開始。 (3)プロト銀河のコラプスでダークマター、ガス、星がビリアル化。 (4)潮汐力、ショックで雲が破壊される。星形成は抑えられる。 (5)回転軸方向の崩落は続くが、動径方向は各運動量輸送タイムスケール。 (6)ガスの安定形状は圧力支持型に緩めの回転が加わった厚い円盤。 (7)そこで出来た星はその運動と形状を保持する。 (8)残ったガスと放出された高メタルガスは冷えて薄い円盤を作る。 (9)プロト銀河コラプス以前に出来た星は楕円体を作る。 |