Anisotropy of Constituents of Interstellar Grains

　アブストラクト

　１．イントロ　

　２．VI Cyg No.12 の SED　

CVF 観測　 　図１には VI Cyg No.12 と BN の SED を示す。2 - 4 μm データは Mt. Lemmon の 60" 望遠鏡＋ InSb CVF(Δλ/λ=0.01) による。 Cyg No.12 の 8 - 13 μm データはキットピーク 2.1 m + CVF (Δλ/λ=0.02)、 BN 8 - 13 μm データは Gillett, Forrest 1973 から採った。 　VI Cyg No.12 の赤化　 　結果は図２に示す。 VI Cyg No.12 に対しては観測データを 10,000 K 黒体輻射で 割った。2 - 4 μm 帯は F(4μ) = 1 とし、8 - 13 μm 帯は F(13μ) = 1 と規格化した。λ < 4 μm での赤化は明らかである。 　BN の赤化　 　BN の 2 - 4 μm 帯は 675 K 黒体輻射で割って F(4μ) = 1 とし、 8 - 13 μm 帯は 500 K 黒体輻射で割って F(13μ) = 1 とした。 割り算に使った黒体とその温度は単に見易さのためであり、物理的意味は含まれない。 　BN 10 μm 吸収帯モデル　 　星の固有スペクトルを Gillett et al 1975 の黒体(モデル１)と仮定したのと、 シリケイト放射(モデル２)と仮定した例を示す。 VI Cyg No.12 のモデル　 　 VI Cyg No.12 には Soifer 1975 のベストフィット黒体モデルを示す。 最終結果は表１にまとめた。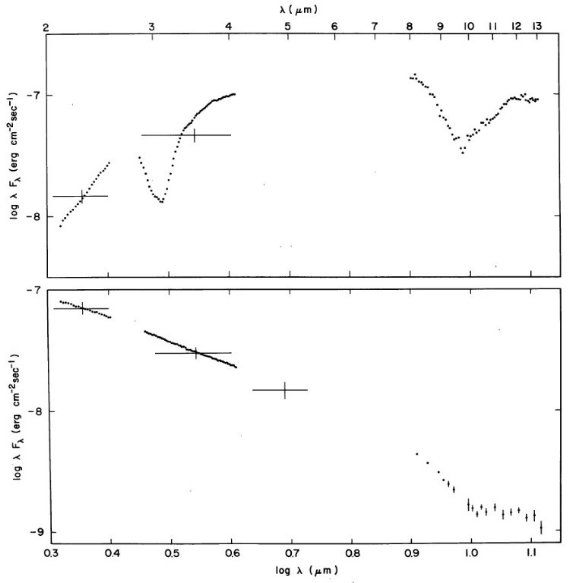 図１．上：BN と 下： VI Cyg No.12 のスペクトルエネルギー分布。

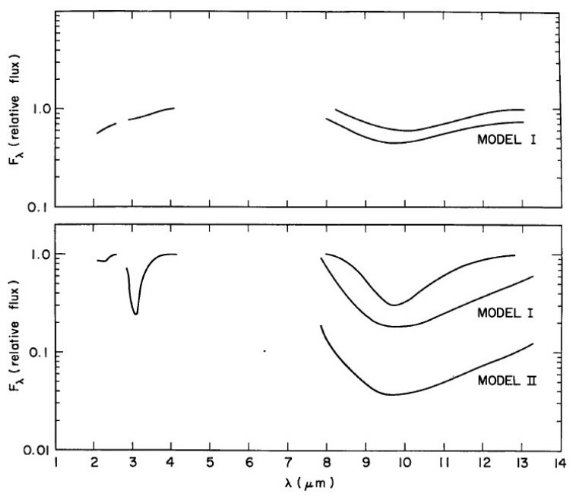
3 μm 帯吸収　 　VI Cyg No.12 の 2 - 4 μm 帯には吸収は見えないが、光学定数の形で 解析すると、減光曲線は 3.4 μm で勾配を変化させる。また τ10μm/τ3μm は 2 - 4 μm 帯と 8 - 13 μm 帯の規格化に依存するが、表１をみると この比は不確定性の範囲内でほぼ１である。 　付着水分　 　VI Cyg No.12 の 2 - 4 μm 帯には幅広のＳＥＤ低下が認められる。 これはダストに付着した水分のせいかも知れない。 表１．VI Cyg No.12 と BN の吸収帯光学的深さ 図２．上：VI Cyg No.12 と 下： BN のスペクトルエネルギー分布の 吸収バンド。観測データを黒体輻射で割り、規格化した。単純なモデルフィット も示す。

　３．議論　　

３．１．氷 - シリケイトの非等方性　　 　VI Cyg No.12 と BN とでは可視減光の強さでは同じくらいなのに VI Cyg No.12 方向に氷吸収は見当たらない。スペクトルフィットから 得られる氷の光学的深さの上限は τ(ice) < 0.02 である。 　定量的に表すと、 τ(氷)/τ(シリケイト)(BN) ≥ 15 τ(氷)/τ(シリケイト)(VI Cug No.12) BN の吸収は主に分子雲により、一方 VI Cug No.12 はより希薄なガス雲に よる吸収が効いている。 　３．２．グレイン成分の質量コラム密度と可視減光　　 　氷の光吸収係数 　3.07 μm での氷粒子による光吸収係数をミー計算で求めた結果は 　1.4 × 104 cm2gm-1 である。 光学定数は Irvine,Pollack 1968 を使った。 　シリケイトの低い光吸収係数 　シリケイトの場合、 10 μm での値は 3000 - 10,000 cm2gm -1 になる。低い 3000 という値は砕いたシリケイトの実験室測定値 と月のシリケイト物質の複素誘電率 Knacke,Thompson 1973 を用いた計算値の二つ である。砕いた粒は大きすぎて飽和効果を引き起こした可能性がある。さらに 月の石の光学定数の測定法には疑問が呈された(Day et al 1974)。 　シリケイトの高い光吸収係数 　 　高い値は純粋なシリケイト光学定数を用いて得たミー計算から得られた。 しかし、吸収プロファイは観測と全く合わない。その上、それらの資料、水晶や フォーステライト、を十分細かく砕いて実験室で測定した吸収率は同じ物質の ミー計算の約半分にしか達しなかった。これらを勘案すると、星間シリケイトの 吸収係数としては 5000 - 10,000 cm2gm-1 とするのが よいであろう。 　様々なシリケイトの混在または非結晶シリケイト　 　様々なシリケイトが混在するとピーク位置が異なるため結果として全体のピーク値は下がる。 また　Day 1974 が作成した非結晶質シリケイトの吸収プロファイルはより観測に合う。しかし その光学定数、または質量吸収係数は得られていない。

コラム密度　 　この論文では氷が 3.1 μm で 1.4 × 104 cm2gm-1, シリケイトは 10 μm で 5×103 - 10×103 cm2gm-1 を使用する。 連続光モデルと κ の選択により値は変わるが、コラム密度は BN で 　　Ssil=(1-7)×10-4gm cm-2, Sice=10-4gm cm-2 Cyg12 で 　Ssil=(7-13)×10-5gm cm-2, Sice≤7×10-7gm cm-2 である。また、可視減光と 10 μm帯ピーク光学的深さの比は 　　Av/τpeak = 14 となる。 この値は Rieke 1974 の求めた Av/τpeak = 24±4 より少し小さい。 　可視減光の評価　 　シリケイトグレインのコラム密度から可視減光を求める際に Huffman,Stapp 1971 の エンスタタイト光学定数を用いてミー計算を行った。計算結果は吸収断面積が粒子半径 a に強く依存することを示している。２種類のサイズ分布を仮定して求めた可視減光量を 表２に示す。これを見ると、シリケイトのコラム密度 Ssil=(7-13)×10-5gm cm-2 に対応する可視減光量は 2.5 - 5 mag 程度である。つまり、シリケイトによる 可視減光は全体の 25 - 50 % しか説明できない。 　クラマース・クロニッヒ関係からも不足が示唆される。　 　Purcell 1969 はクラマース・クロニッヒ関係を適用して、観測減光量を 生み出すのに必要な最低コラム密度 S を導いた。誘電体のグレインに対してはこの値は 　　　 S > 7.7 × 10-6 &rho:gDkpcAv gm cm-2 である。ここに Dkpc は kpc 表示の距離である。 VI Cyg No.12 までの距離を 2.1 kpc とすると、 　　　Ssil > 4.9×10-4gm cm-2 であり、これからも 10 μm 吸収帯強度からはシリケイトは可視減光の 25 % しか 説明できないという結果が再び得られた。 ( K-K 関係からの結論は観測減光量を出すための 最低コラム密度がシリケイトの推定コラム密度の４倍になるということらしい。) 表２．エンスタタイト可視減光のパラメタ―

　４．結論