
| 太陽近傍の非常に明るい M-型巨星 97 個の高品質「固有」スペクトル λ = [380, 900] nm を得た。Case と MK 分類で M-型のサブタイプ 全てが含まれている。結果は λ = [99, 12500] nm の測光合成スペ クトルにフィットされて、対応連続光分布を推定した。 | 恒星スペクトルは固有スペクトルとも比較された。有効温度が導かれ、 数学的なスペクトル分類基準が見出された。 (UB)j, (VRI)c, (JHKLM)ESO 測光値も与えた。データは CDS で得られる。 |
|
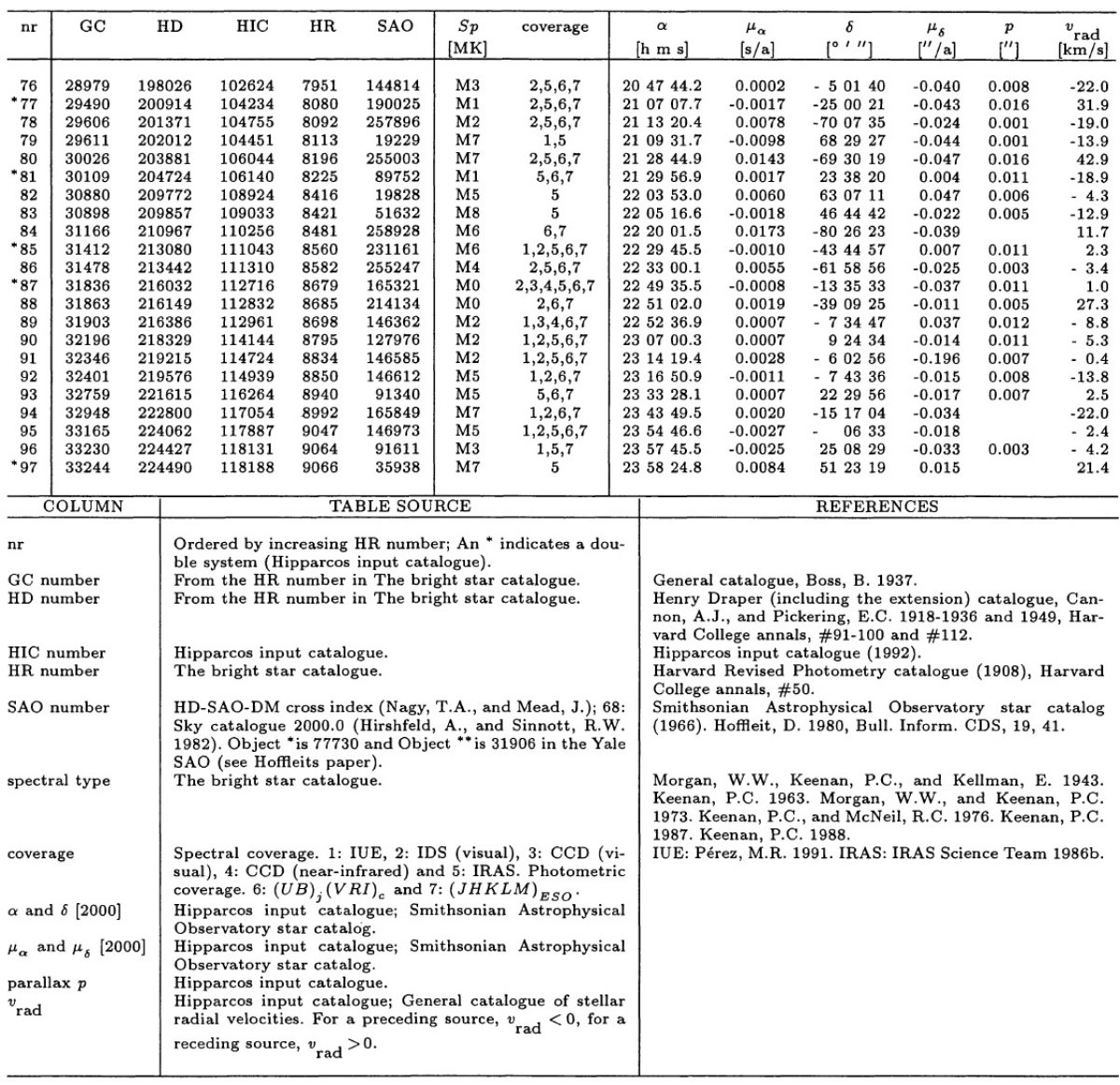
天体選択 ヒッパルコスで観測される予定の Bright Star Catalogue 星の中から、97 個の M-型星を選んだ。それらは表1に載っている。表には GC. HD, HIC, HR, SAO カタログ番号、MK スペクトル型が載っている。そこには座標、視差、 視線速度も載っている。 平均 M-型星スペクトル 観測から統計処理を行い、平均 M-型星スペクトルを決めた。 |
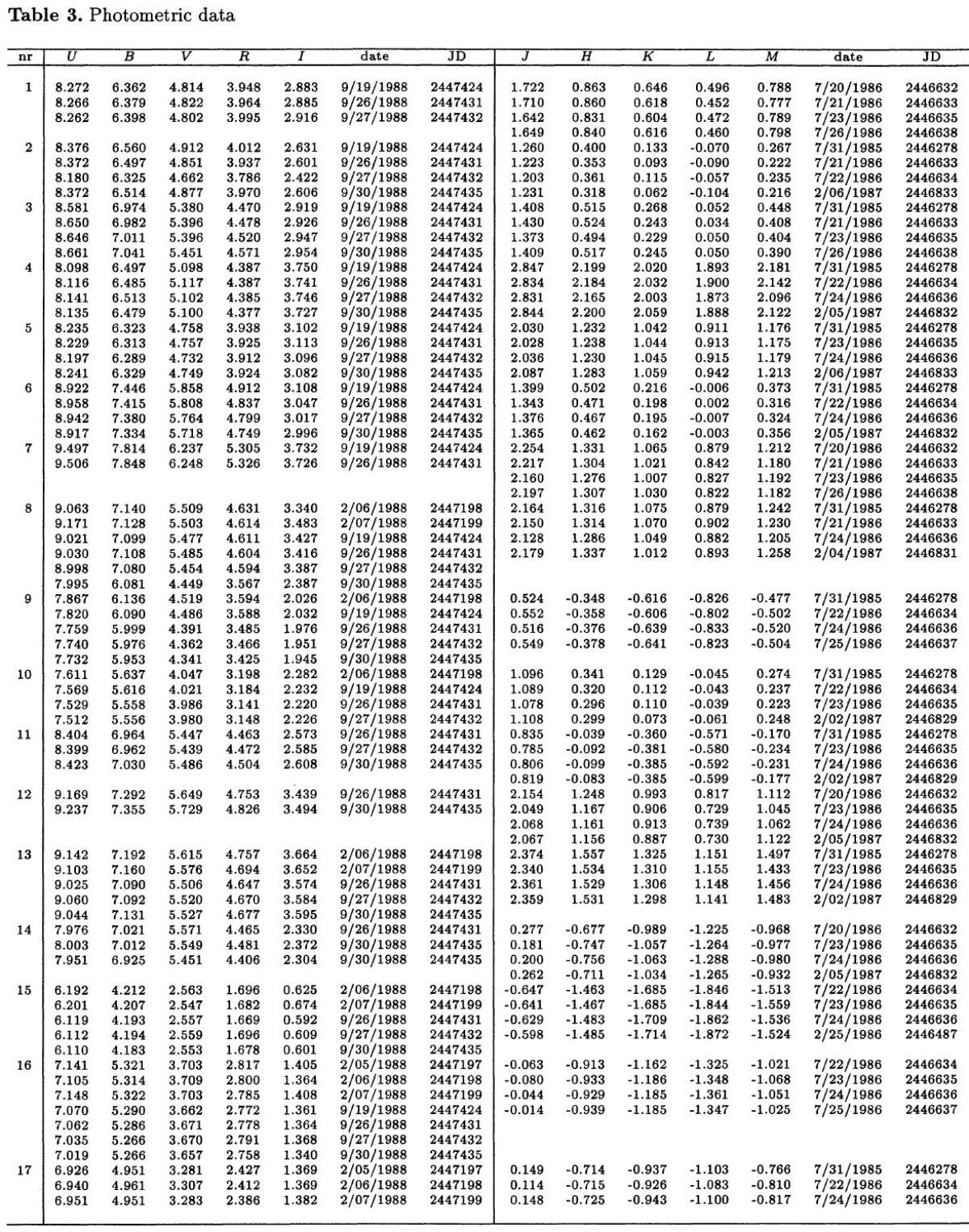
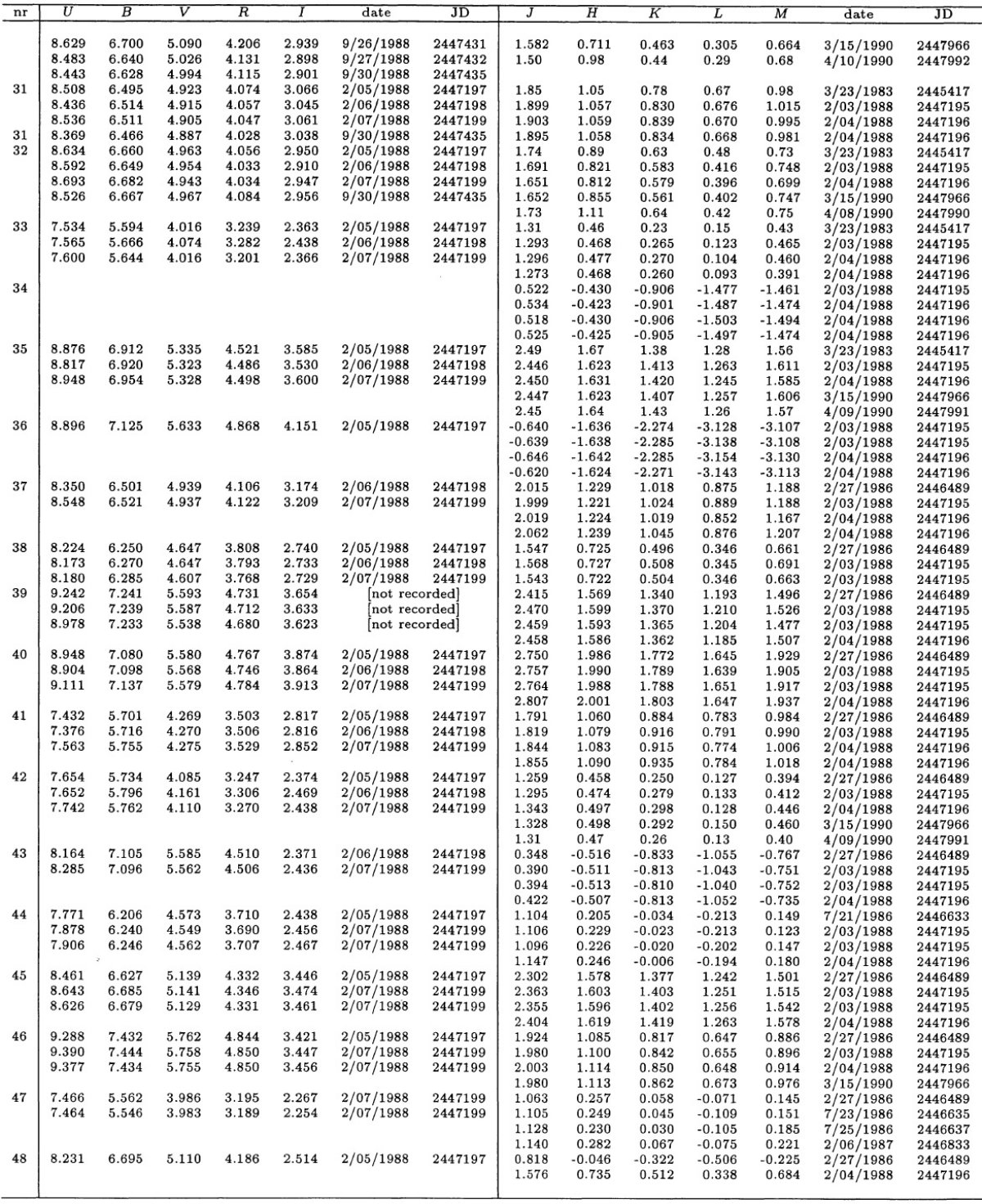
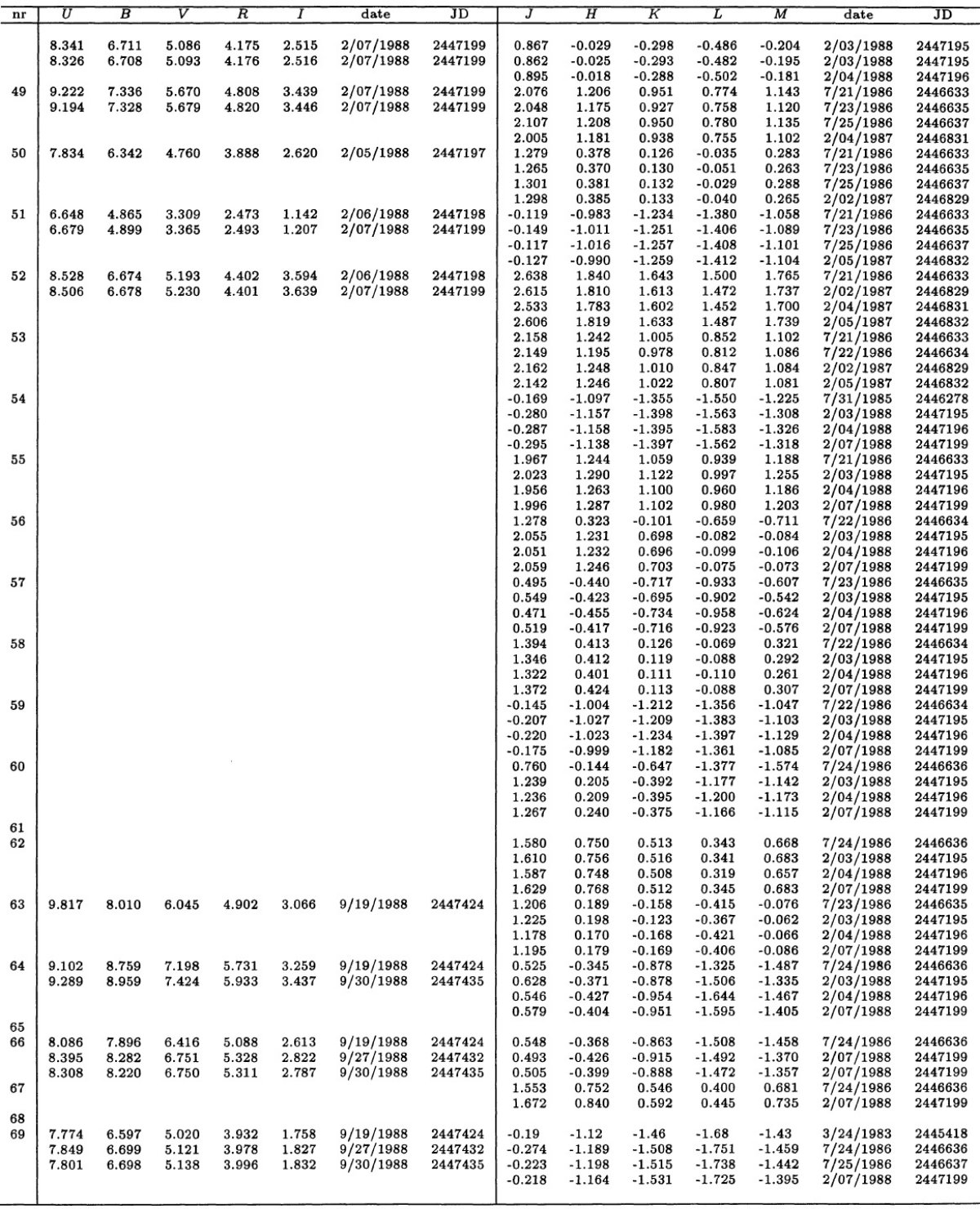
過去の研究 可視域での M-型巨星のスペクトル研究は Moreno 1973, Guterrez-Moreno et al 1982, Turnshek et al. 1985, Silva, Cornell 1992 により行われた。 近赤外スペクトルは Lancon, Rocca-Volmerange 1992 により 1428 - 2500 nm で研究された。 測光 スペクトルデータは表3にある (UB)j, (VRI)c, (JHKLM)ESO 測光結果で補足された。 |


|
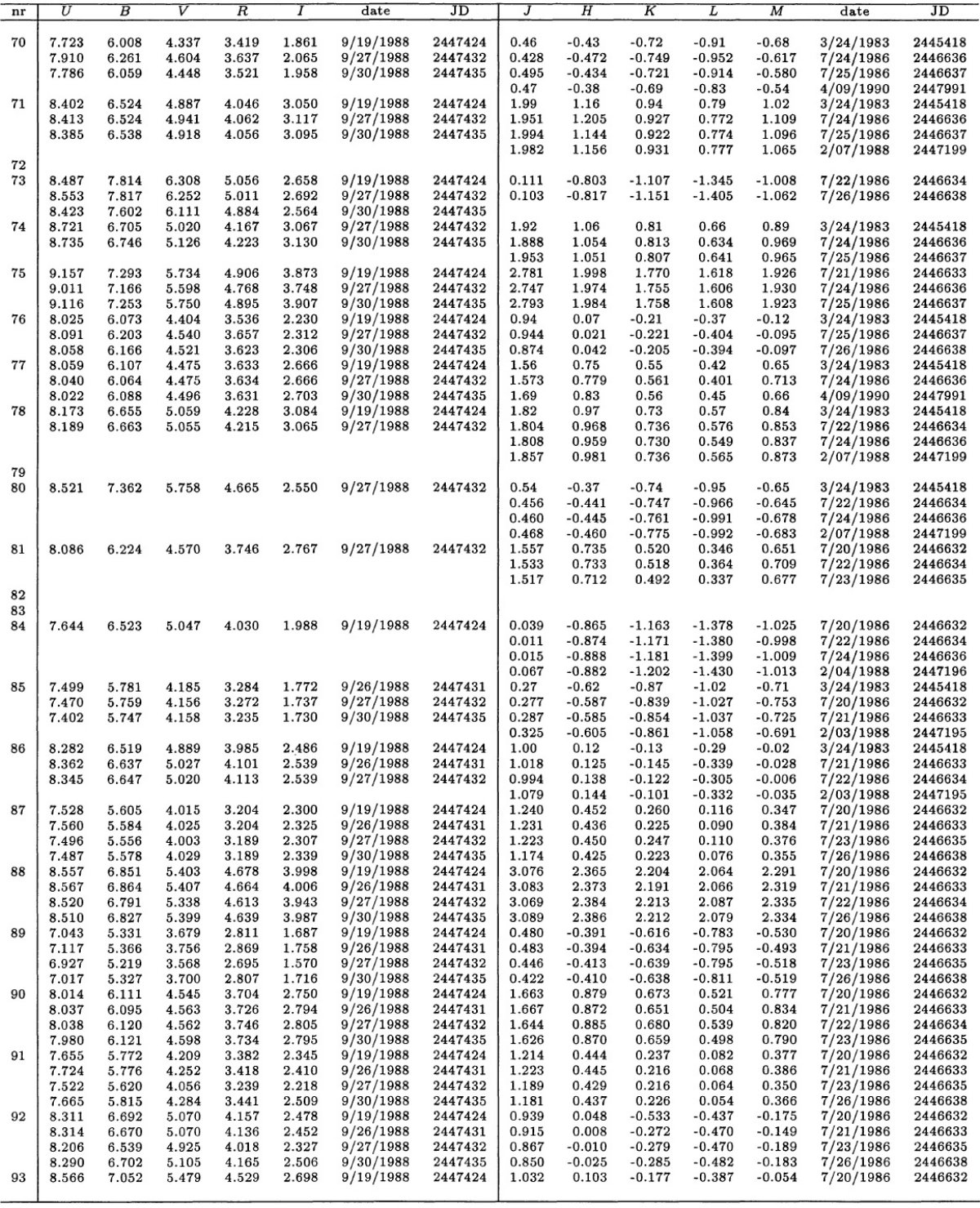
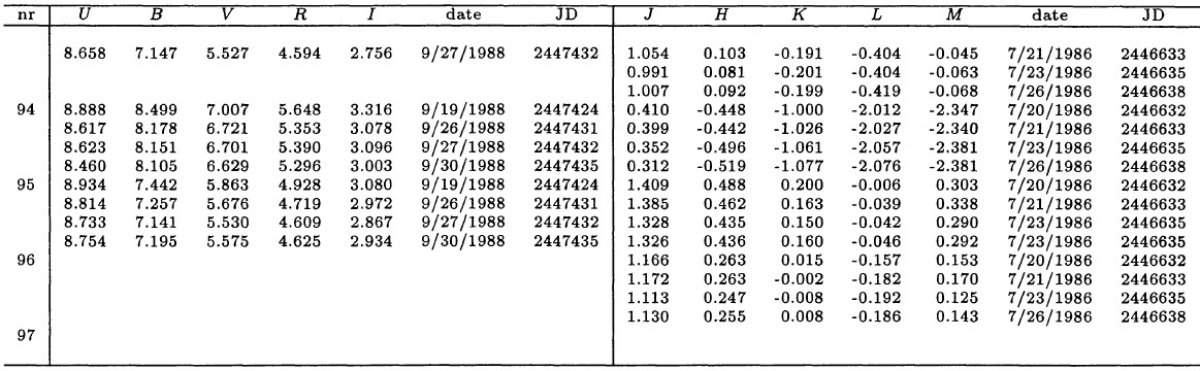
Feast et al 1990 との重複 40/97 星は Feast et al 1990 と重複している。表3には観測者と日付を載せた。 2.1.分光観測とデータ処理装置ESO 1.52 m 望遠鏡に Boller-Chivens 分光器を付けて λ = [380, 900] nm スペクトルを撮った。ESO#13 CCD (RCA 5264-16-7 チップ) を使った。 分解能は R = 1300 - 9000 である。S/N は非常に良い。分光器のスリットは 5" x 240" である。 ESO 観測 データ処理は MIDAS で行った。フラックス較正には Heydari-Malayeri et al 1989 の App G から採った 5 個の白色矮星スペクトルを用いた。それは Oke 1974, Stone, Baldwin 1983 の狭帯測光に基づいている。スペクトルは 大気減光とスリット通過ロスを補正(Fluks, The 1992a, 1992b)した。 こうして 42 星の [380, 900] nm スペクトルを得た。それらのデータは [380, 680] nm イメージ・ディセクタース・キャナースペクトル、IRAS, IUE データで補足された。 2.2.測光観測(UB)j, (VRI)c 等級(UB)j, (VRI)c 等級は ESO 50 cm 望遠鏡に 搭載した RCA 31034A フォトマルによる光電測光で得られた。アパーチャ直径は 15" である。測光標準星は Menzies et al 1980 のリストを用いた。 (JHKLM)ESO 等級 (JHKLM)ESO 観測は La Silla ESO 1 m 望遠鏡に搭載した InSb 測光器を使用して行った。13" ダイアフラムが用いられた。標準星は Koorneef 1983a を用いた。フィルターは ESO で一般的に使用されている物で ある。 |
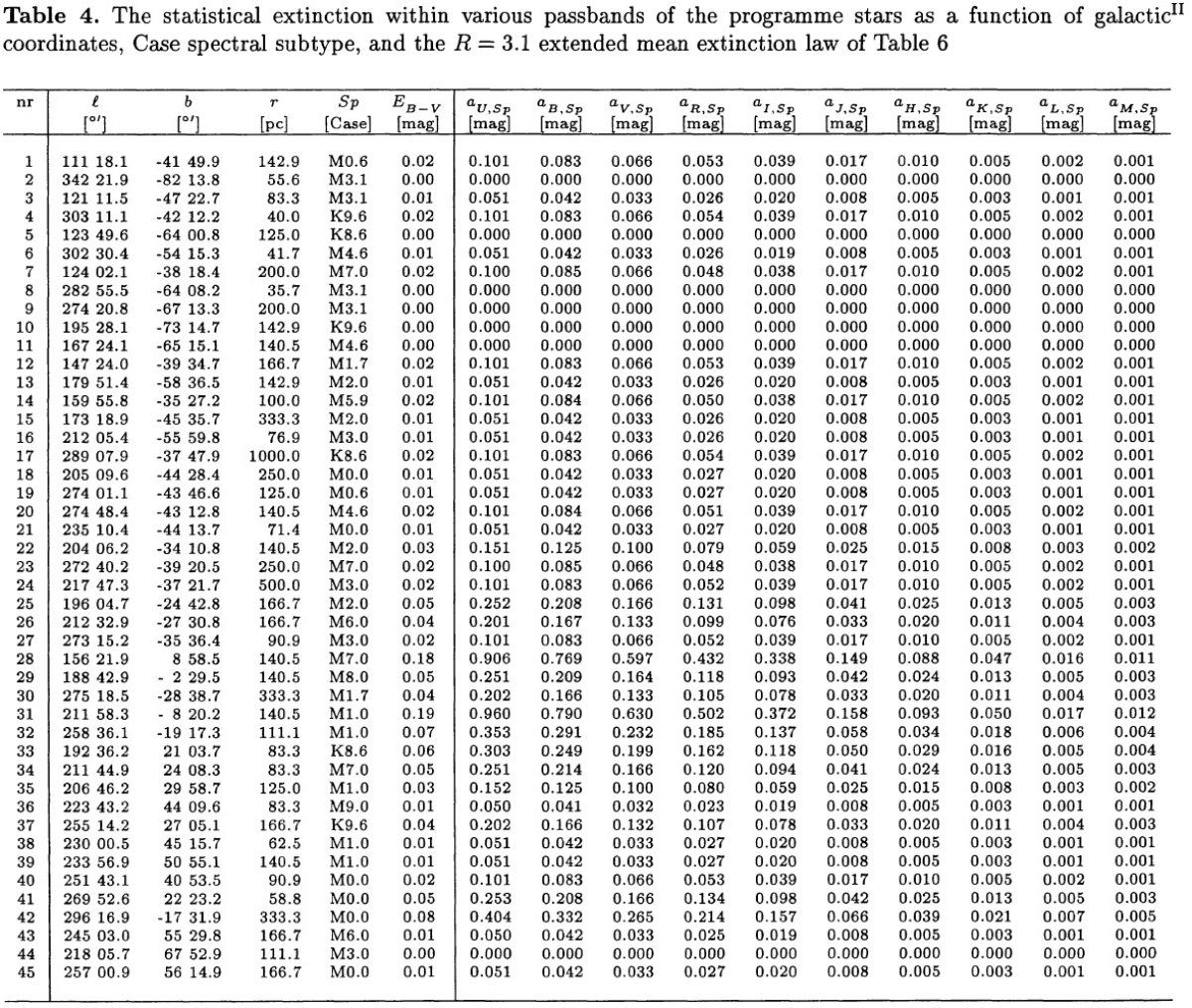
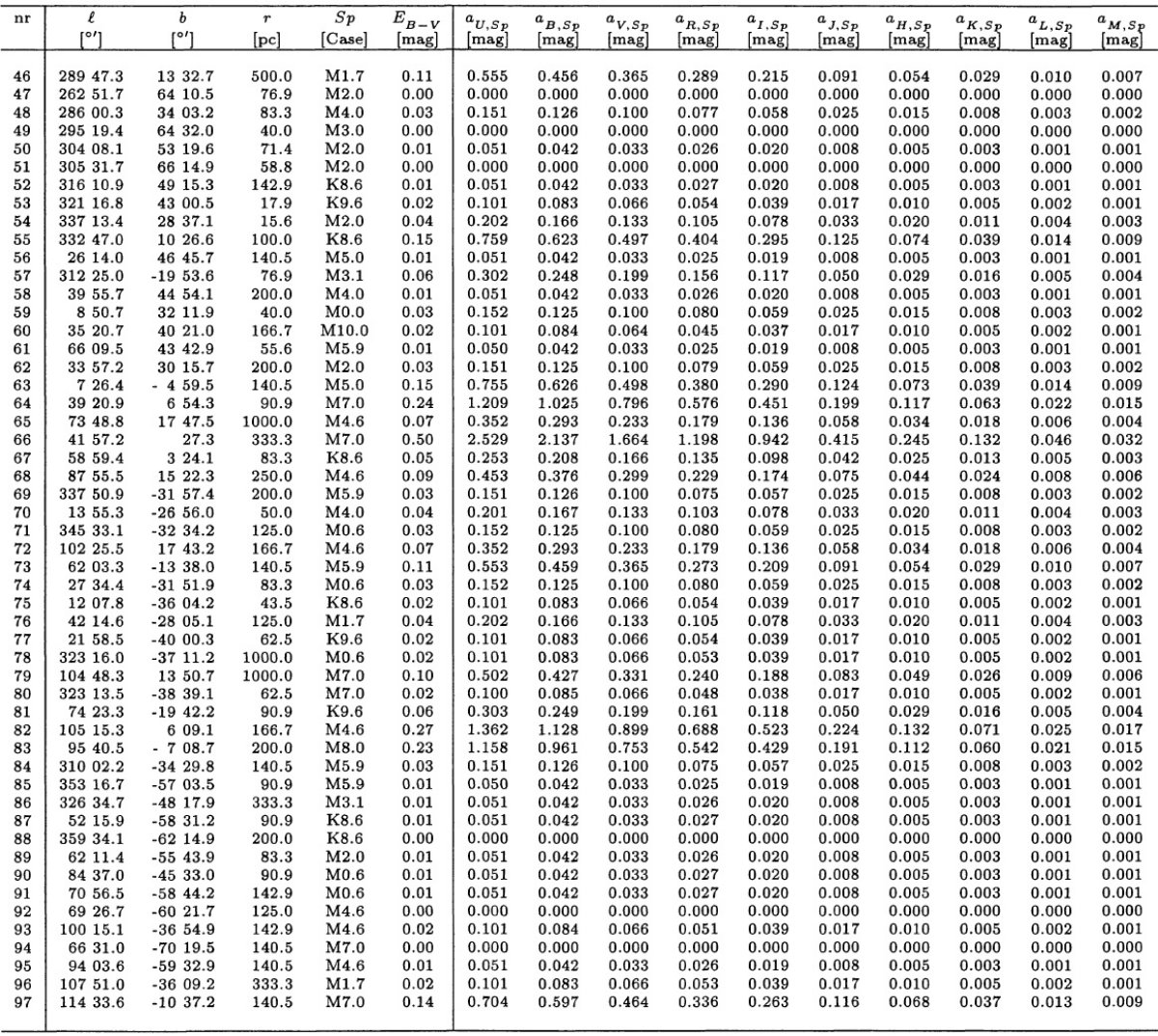
 表2.ESOにおける観測者と日付 データ処理は SNOPY により行われた。観測結果は表3に示されている。 赤化補正は施されていない。しかし、各バンド内での減光の統計的評価を 表4に示した。
ここに、Sx は X-バンド内の応答関数、F(λ)Sp は固有スペクトル、χie(λ) は減光関数、つまり 星間空間を通過した輻射の割合である。 |
|
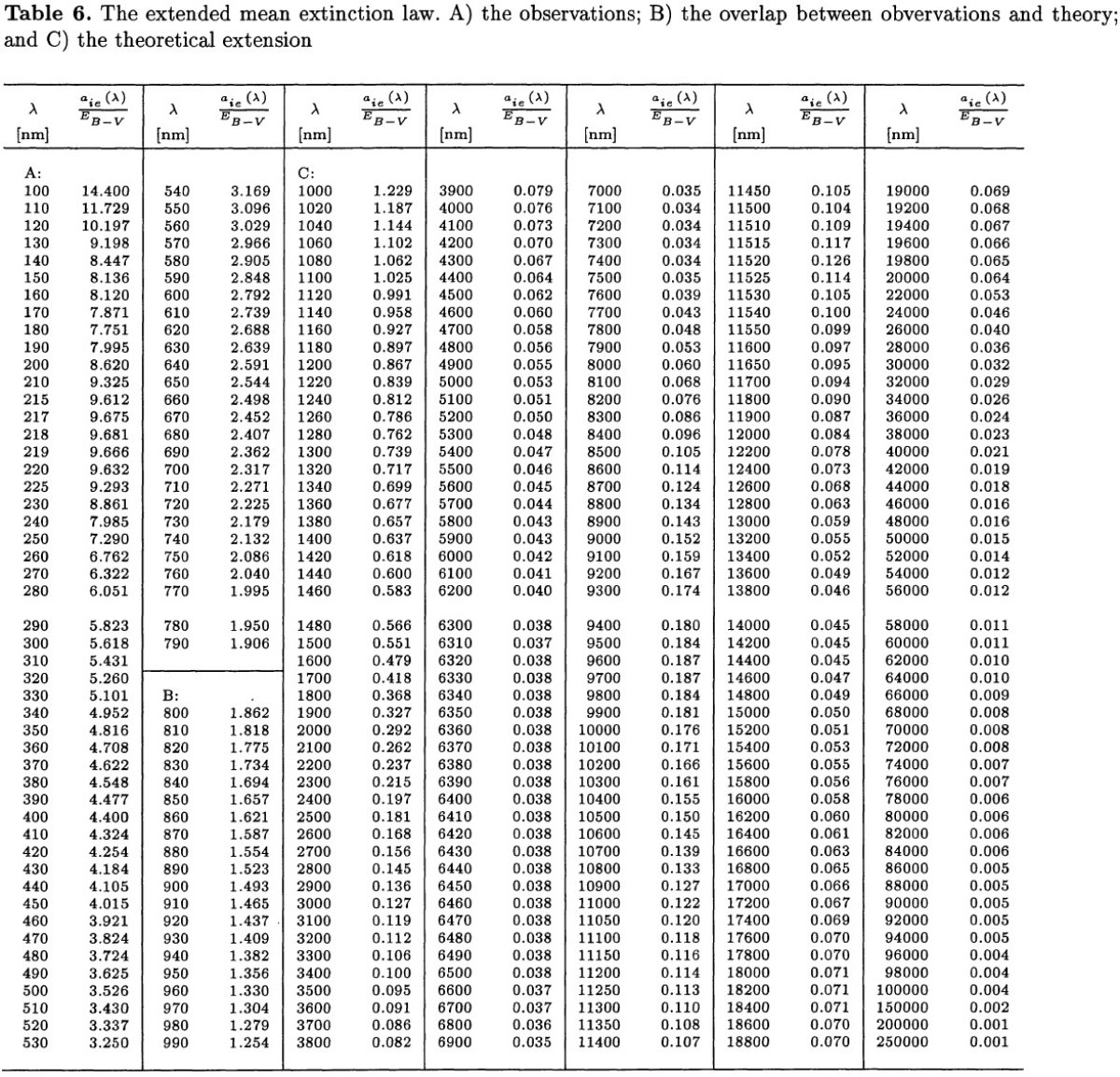
INSTEXNM MIDAS には星間減光テーブル INSTEXNM が内蔵されている。このテーブルは上限が 1090 nm である。それより長波長が必要な場合、拡張版の NEWINTEXNM.TBL が 用意されている。これは Savage,Mathis 1979 の観測減光則に基づき、Steenman, The 1989, 1991 のモデル減光則により計算された。それは粒子半径 [4, 220] nm, n(a) ∝ a-3.5, グラファイト量がシリケイトの 1.12 倍を仮定して いる。減光則の主要部は表5に示されている。 長波長側の拡張減光則 λ = [100, 800] nm での減光は観測平均減光則を用いた。 λ = 1000 nm より長波長側は理論モデル、[800, 1000] nm は 両者を滑らかにつないだ。 短波長側 単波長側では減光は主に星間グラファイトとシリケイトのミー散乱による。 その結果は図1と表6に示す。 |
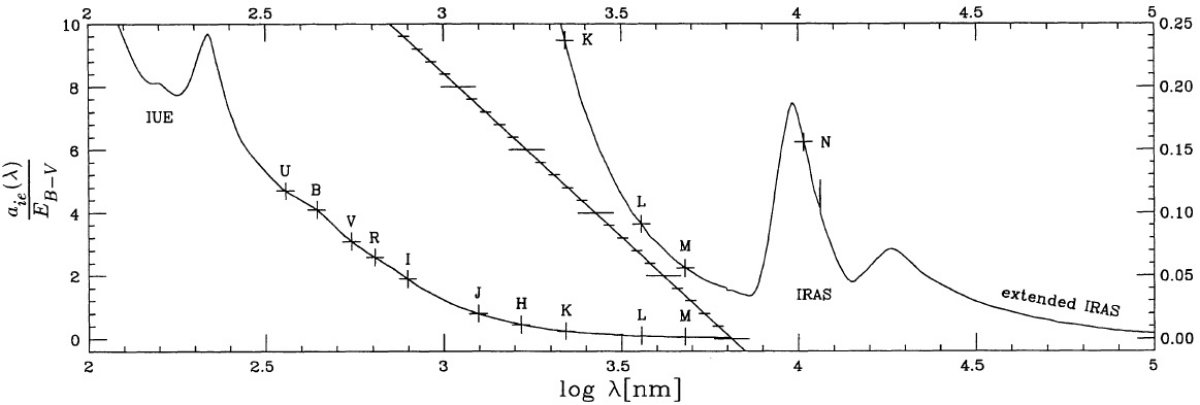
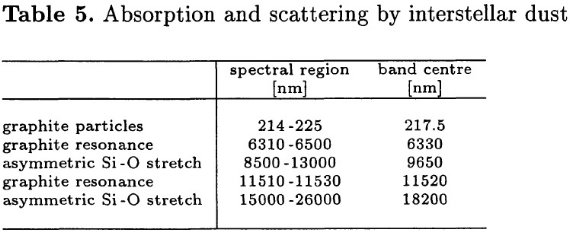 表5.星間ダストによる吸収と散乱。 図1=減光則 図1に減光則をグラフで示す。 (1)IUE スペクトルは単波長側では青化を受け、長波長側で赤化を示す。 (2)ESO (L-N), (M-N) カラーは弱い青化を示す。 (3)IRAS スペクトルは赤外部で青化、遠赤外で赤化を受ける。 |
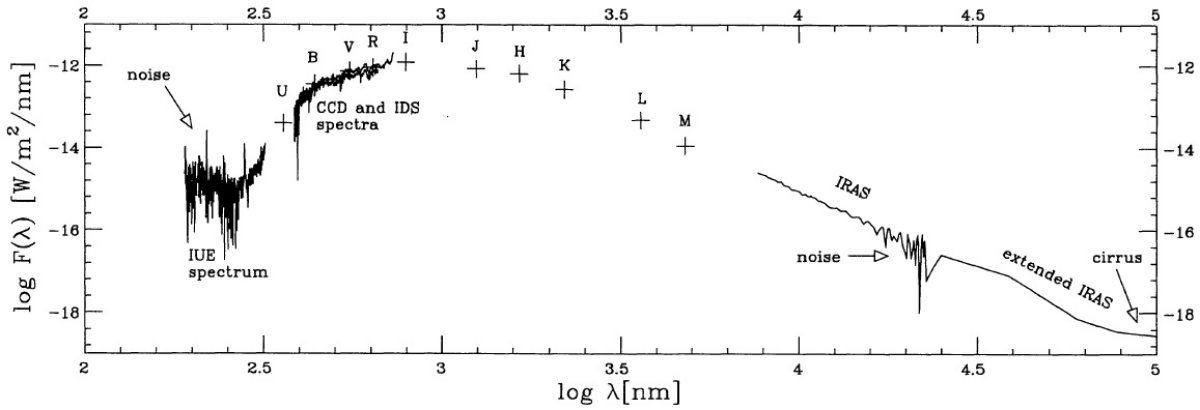
| 通常 M-型巨星は星周ダストに囲まれている。その結果それらのスペクトルは 星周減光を受ける。λ < 1000 nm では星周吸収や星周散乱を受けるが、 λ > 1000 nm では黒体に近い星周放射が生じる。 | しかし、図2にはどんな赤外超過も見られない。僅かに弱いシラス放射が ありそうなだけである。それは他のサンプル星でも同様であった。このように、 我々が選択した M-型巨星では星周ダストに関する補正は必要ない。 |
|
写真スペクトル分類との対照が必要 M-型星のスペクトル分類は吸収帯に基づいて行われる。数学的な 基準に基づいて、サブタイプを決める方法が望まれる。過去の分類は 写真乾板上のスペクトルに頼っていたので、CCDデジタルスペクトルを 過去の分類と較べてみることが重要である。 Case システム 我々の分類は Case システム Nassau, Velghe (1964) に依っている。実際の分類では、 (1)Turnshek et al 1985, Silva, Cornell 1992. 較正が不十分。 (2)Case MK 分類関係(2)と (3). (3)今回得たスペクトル を用いる。 |
MSp 関係 Blanco 1964 が発表し、 The et al 1990 が用いたデータから MSpCase - MSMK 関係が分かる。もし、Mt.Wilson と MK サブタイプは同一 FitzGerald 1969, Mikami 1978 とするなら、サブタイプに 次の関係が得られる。 KSpCase = K{Sp MK - 0.7[1 + tanh(0.8(4.4-Sp MK))]+10}) (MSp MK<1.4) MSpCase = M{Sp MK - 0.7[1 + tanh(0.8(4.4-Sp MK))]}) (MSp MK>1.4) この式は早期 M-型星に、系統的な差が存在することを示している。もし、サンプル 星に適当なスペクトルが得られない場合には表1からスペクトル型を得て、それを 上の関係式で Case システムに変換した。表4の第5列にその結果を示す。 |
|
平均スペクトル スペクトル型の順に並んだ観測スペクトル F(λ)* Sp, jから、Sp-0.5 ≤ Sp < Sp+0.5 の k 個 が抜き出される。平均を取る前にまず i-番スペクトル F(λ)* Sp, i の平均(?)レベルに合わせられる。
通常は λl = 450 nm, λu = 857 nm と する。図9のバンド3の終わりが 857 nm である。 統計的減光補正 Feast et al 1990 は次のような赤化式を導いた。
表1の歳差と表4の銀経に基づき個々の星に対し EB-V を求める。 銀河面上の星に対しては、 Neckel, Klare (1980) の減光マップを用いる。距離 r が不明な場合は該当するスペクトルサブタイプ星の 平均距離を採用する。r と EB-V は表4に示す。 次の式で平均赤化を計算する。
|
固有フラックス 固有フラックス F(λ)Sp は観測フラックス F(λ)*Sp と下の関係にある。
ここに平均減光関数 ⟨χic(λ)⟩ は、減光則 と次の関係にある。
複数個スペクトルの場合のエラー 一つのサブタイプに複数個のスペクトルがある場合、星間減光を補正した 平均相対誤差も得られる。データを調べた結果以下の結論を得た。 (1)波長、フラックス較正の誤差はフラックスレベルの規格化による誤差より小さい。 (2)スペクトルの細かい構造に較べノイズは小さい。 サブタイプに観測スペクトルがない場合 サブタイプに観測スペクトルがない場合は内挿を使用した。内挿には幾何学平均 を用いた。テストの結果は許容可能であった。 ( つまり、固有フラックス F(λ)Sp は観測フラックスの平均を 星間空間透過率の平均で補正して得られる。) |
|
モデル大気の計算 スペクトル型 Sp のモデル連続フラックス F(λ)Sp,C が 計算された。計算には大気モデル SOSMARCS (Plez et al 1992) とその水平大気版 POSMARCS を用いた。SOSMARCS は球対称な LTE 大気 で 99 - 12500 nm 間 10912 点で完全オパシティサンプリングを行っている。 Plez et al 1992 のモデルグリッド以降の変化としては、CN レッドシステム オパシティを最近の Jorgensen, Larrsen 1990 による最新版に取り換えたこと である。しかしそれは有効温度を 10 K 変えた程度の影響しかない。TiO γ および γ' システムライン強度も Doverstal, Weijnitz 1992 の新しい測定値に置き換えられた。モデルは太陽組成、乱流速度 ξ = 2 km/s で計算された。暖かい、例えば 3800 K モデルでは球対称と水平モデルとでは 大きな差は生じない。しかし Te = 3000 K になると連続光フラックスに 5 - 6 % の差が可視、近赤外で生じる。250 nm 以下の紫外では、メタルの連続吸収が 高い温度依存性を有するために、ずっと大きい違いが生じる。しかし、そこは この研究の対象ではない。 |
赤色巨星枝のモデル系列 Ridgeway et al. (1980) の有効温度較正を用い、星質量を 1.5 Mo に固定して、Lattanzio 1991 の赤色 巨星枝モデルから有効温度と光度の関係を採って、赤色巨星枝のモデル系列が 得られた。表面重力は Te = 3900 K で log g[m/s2] = -0.40、 2500 K で -2.5 である。 ( Ridgeway et al. (1980) は M6 までしか扱っていないはず。Lattanzio のモデルと SOSMARCS の 二つで十分ではなく、 Ridgway80 を必要とするのはどこでだろう? 図3のようにスペクトル型と対応させたいから?) 合成スペクトルは 10,912 波長点でのフラックスからなる。これは可視域では 間隔 1 A に相当する。Plez 1990 が指摘するように球状大気モデルは与えられた 有効温度に対し、平面モデルよりも晩期のサブタイプとなる。 |
|
各固有スペクトル、すなわち有効温度に対して、合成スペクトルを対数的な
内挿で計算した。Plez et al 1992 によると、合成スペクトルは λ
< 550 nm でフラックスが大きくなり過ぎる。そこで、内挿は λ =
[550, 900] nm に限定した。 F(λ)Sp = F(λ)Sp,Tlα F(λ)Sp,Tu1-α ベストフィットの時に、内挿スペクトルと有効温度 Tsp の固有スペクトルとの 比は平らなスペクトル関数となる。 |
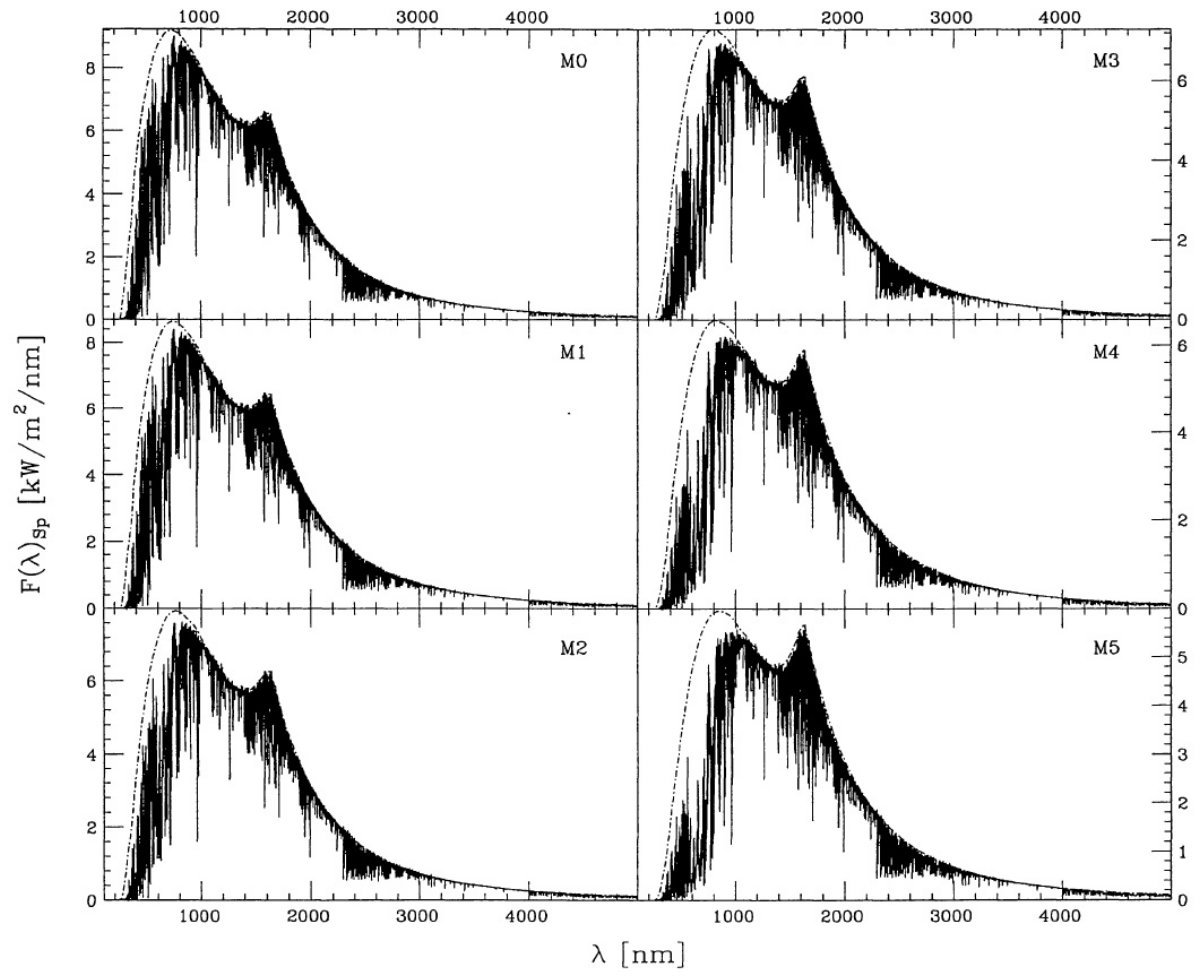
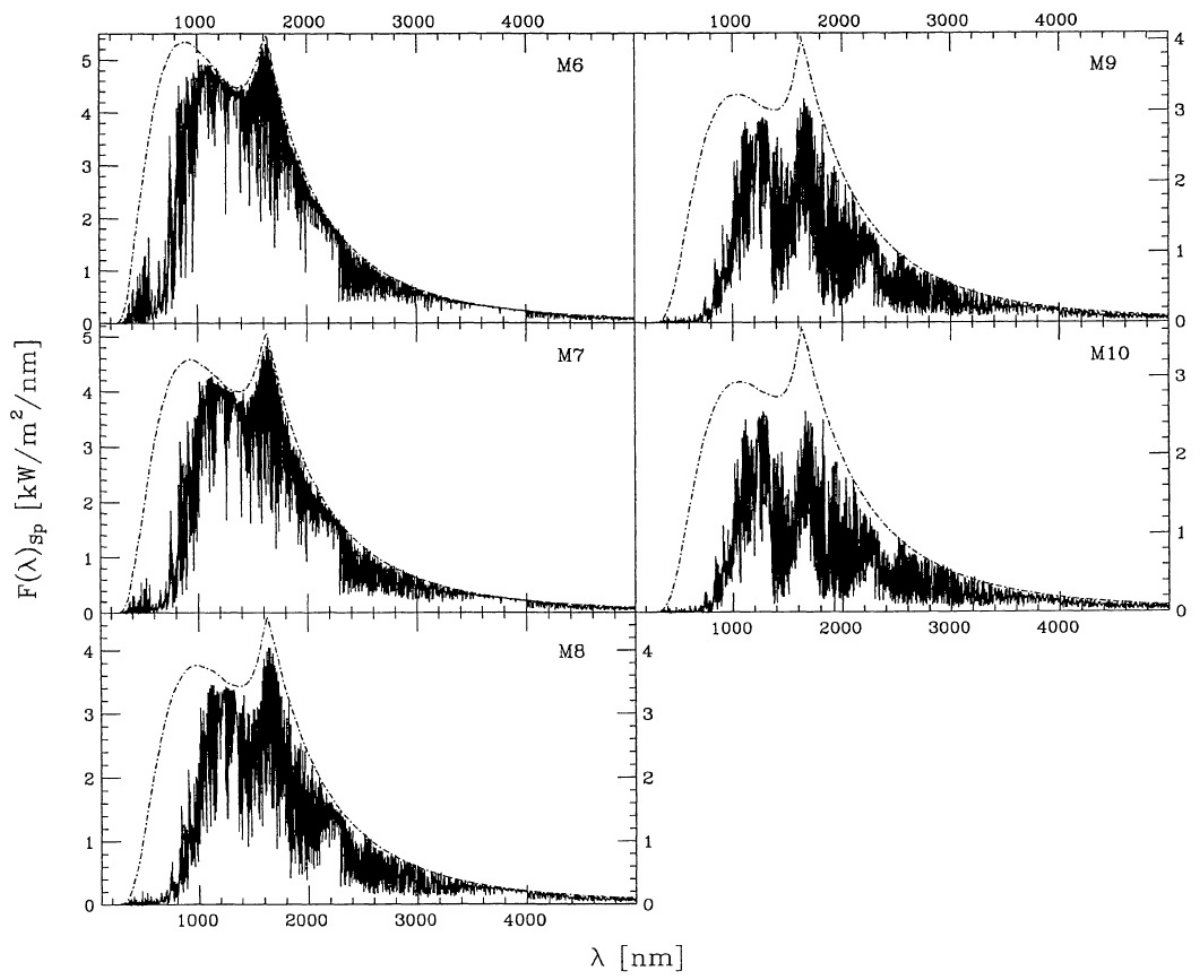
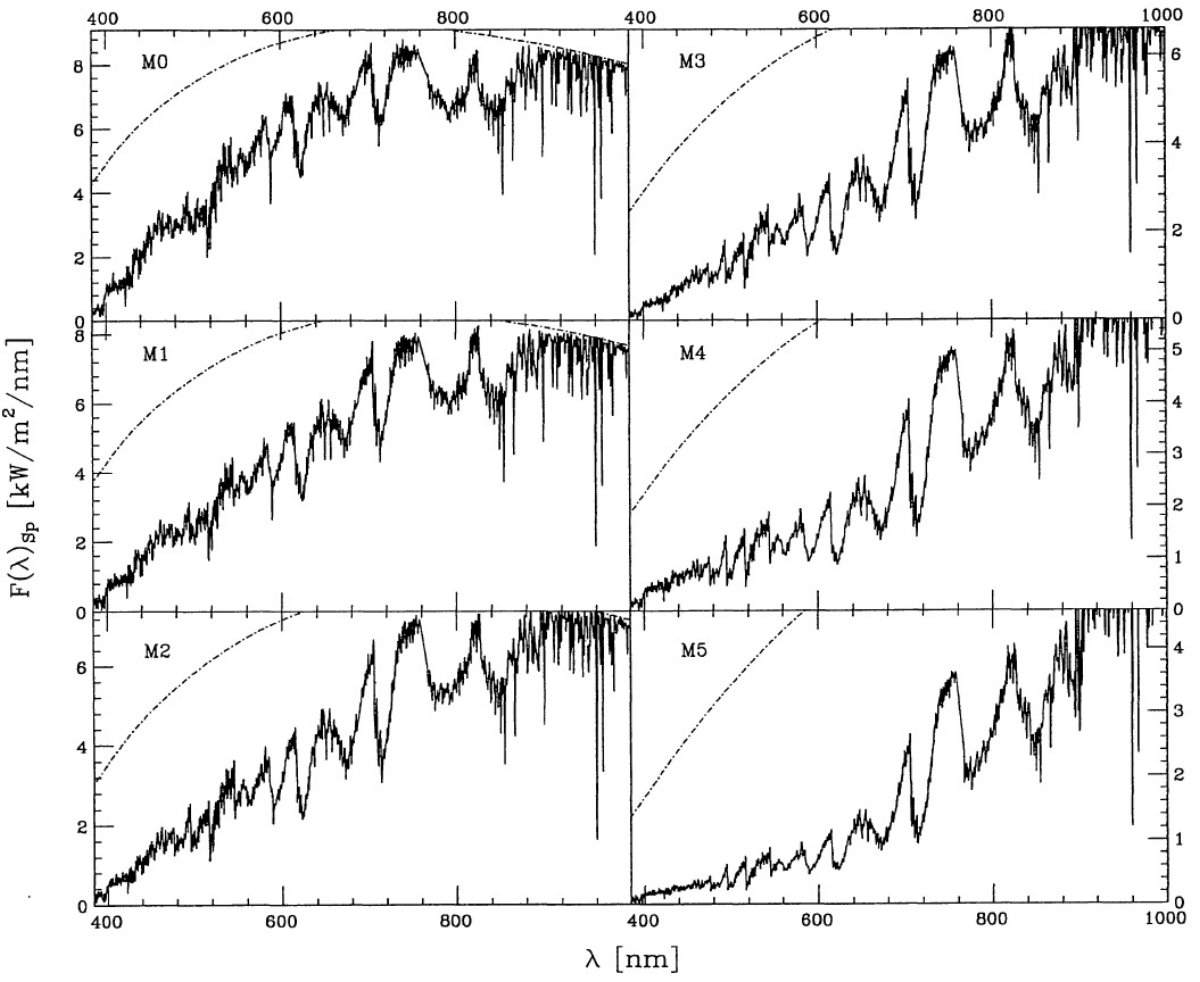
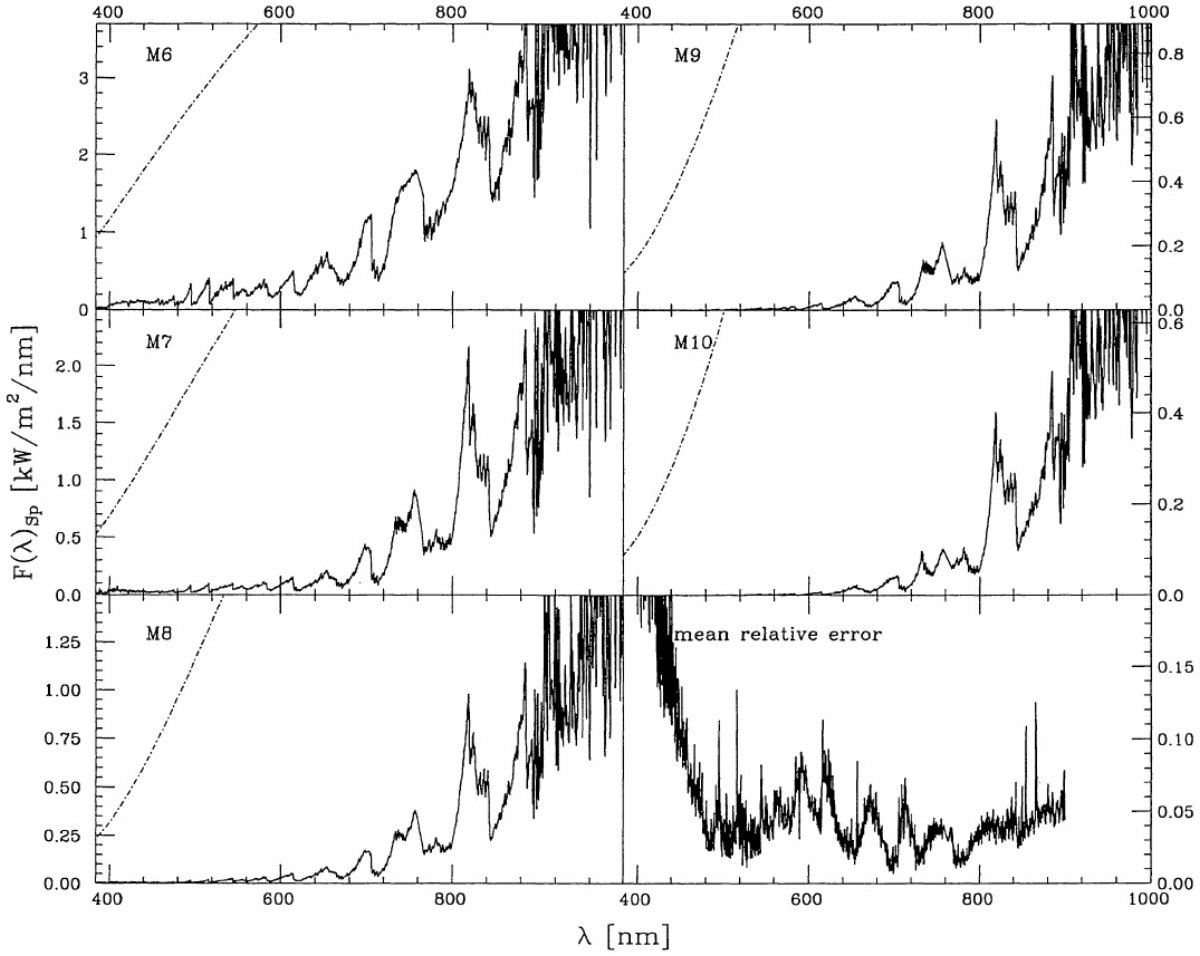
特性固有スペクトルを次のように定義する。
( ここの F(λ)Sp は一つ前の式の F(λ)Sp と同じなのか? F(λ)Sp,Scaled が特性固有スペクトルのことか?) 特性固有スペクトルは図3と図4に示す。 |
|
MK 分類に比べて Case 分類の引用は少ない。そこで、 Case 分類スペクトル
から MK 分類スペクトルを得る手段をここに述べる。 (1)5 章の式で MK サブタイプに対応する Case サブタイプを決める。 表7の第3列に MK サブタイプ、第4列に対応する Case サブタイプを示す。 (2)図5から対応する温度を導く。 (3)M2 - M6 MK 分類固有スペクトルは M0 - M6 Case 固有スペクトルを内挿して 得た。 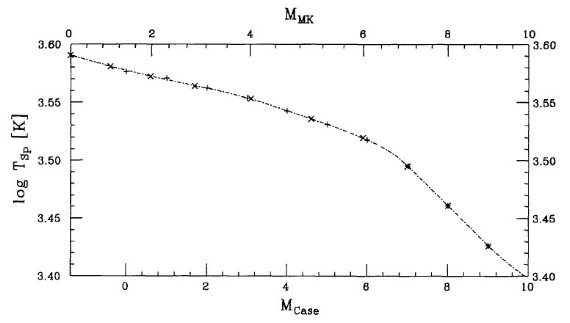 図5.スペクトル型と有効温度の関係 |
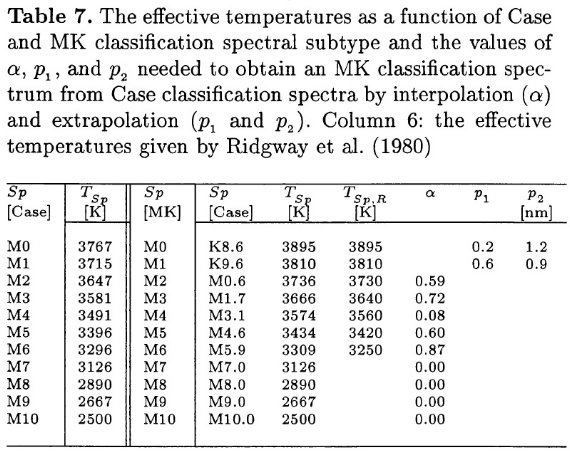 表7.有効温度と Case, MK スペクトル型サブタイプの関係。TSp, R は Ridgway et al 1980 の較正。 |
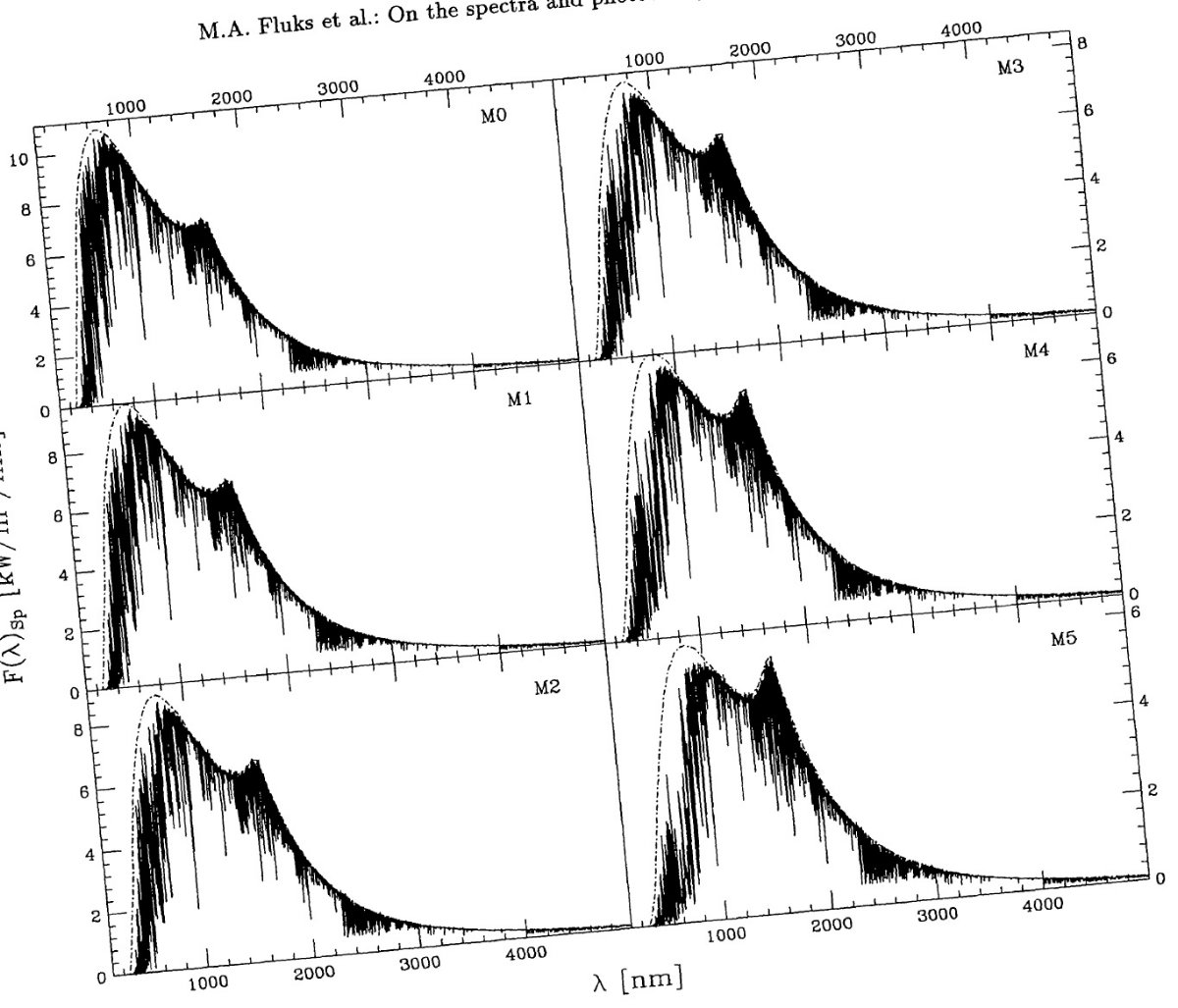
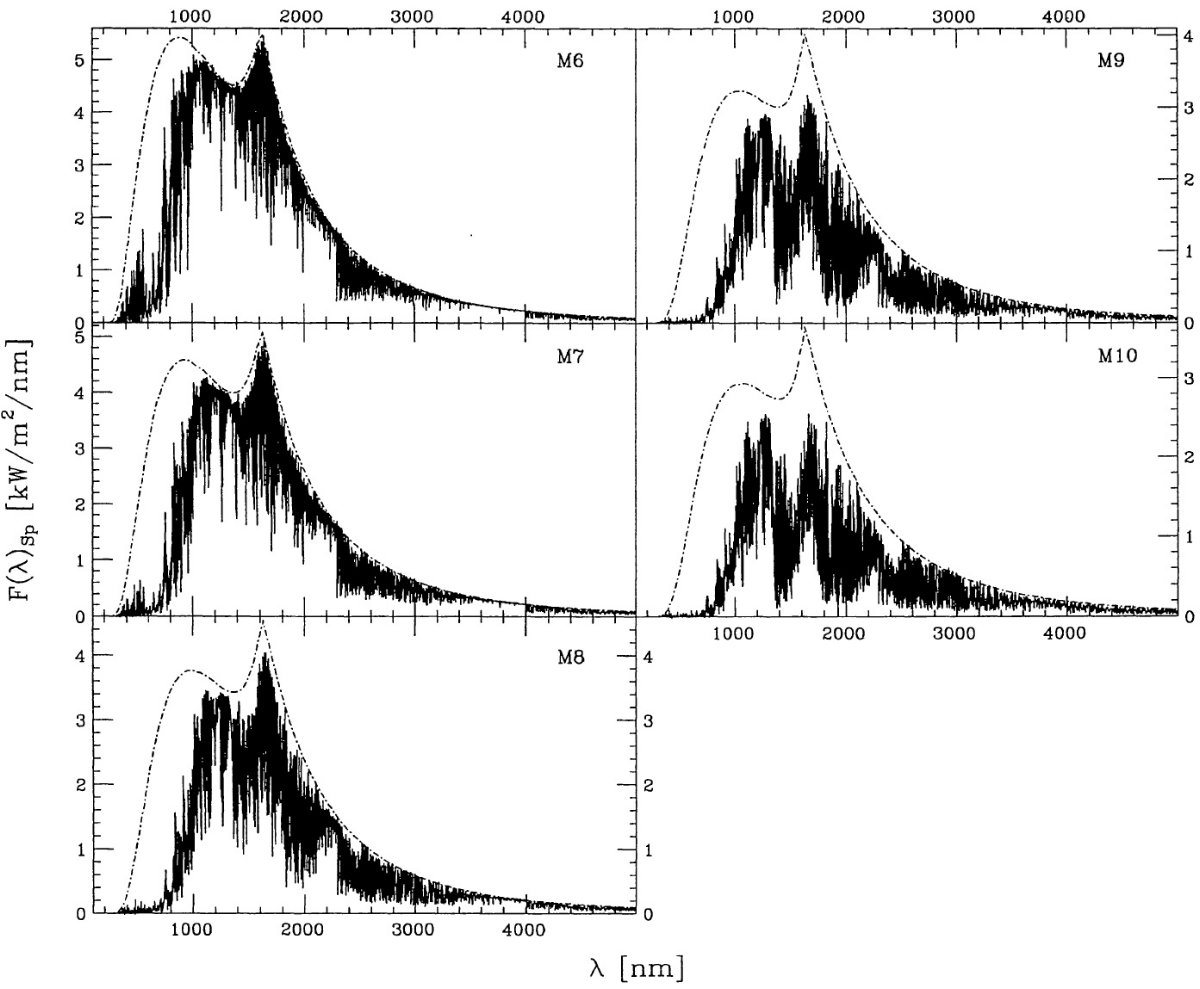
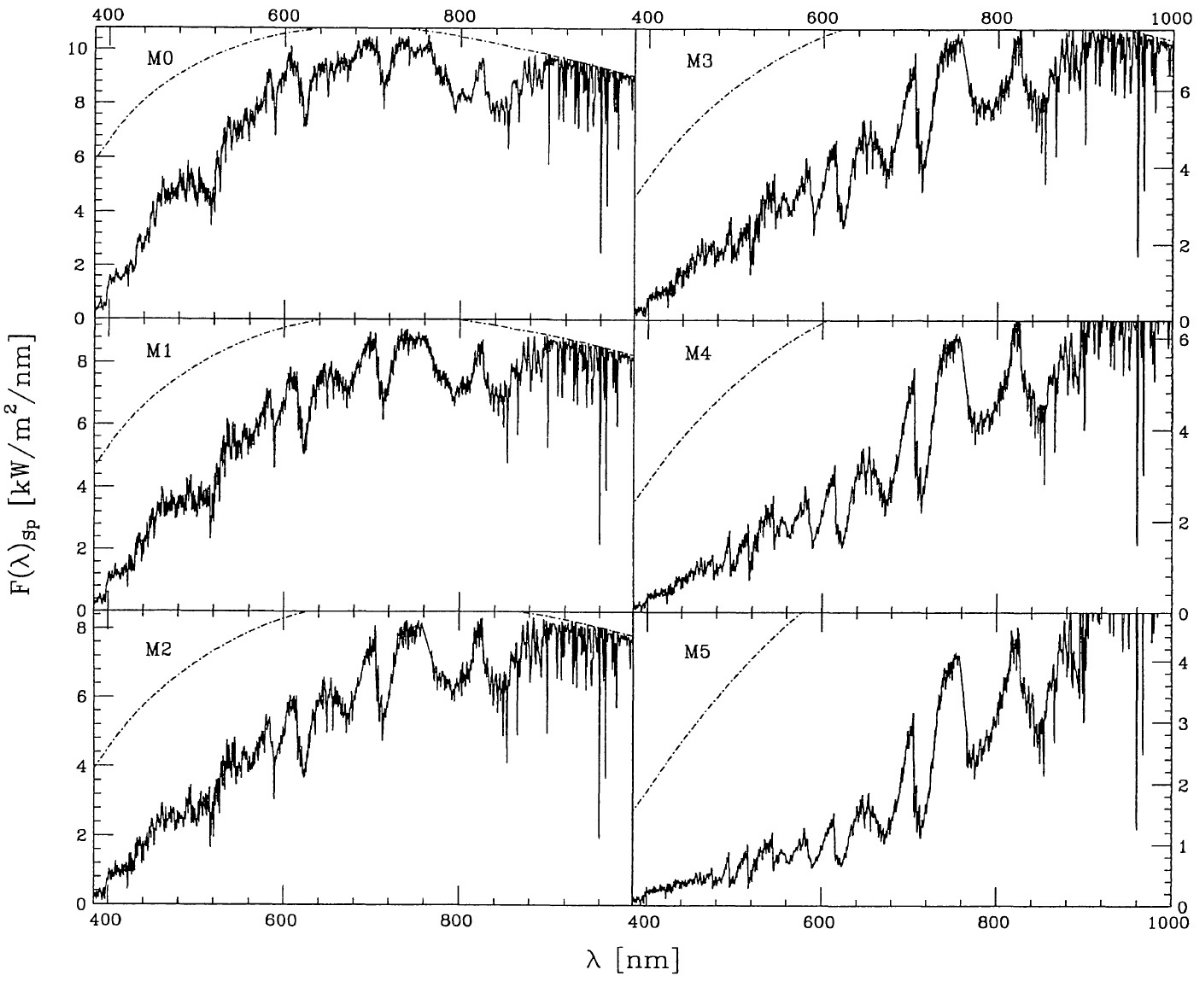
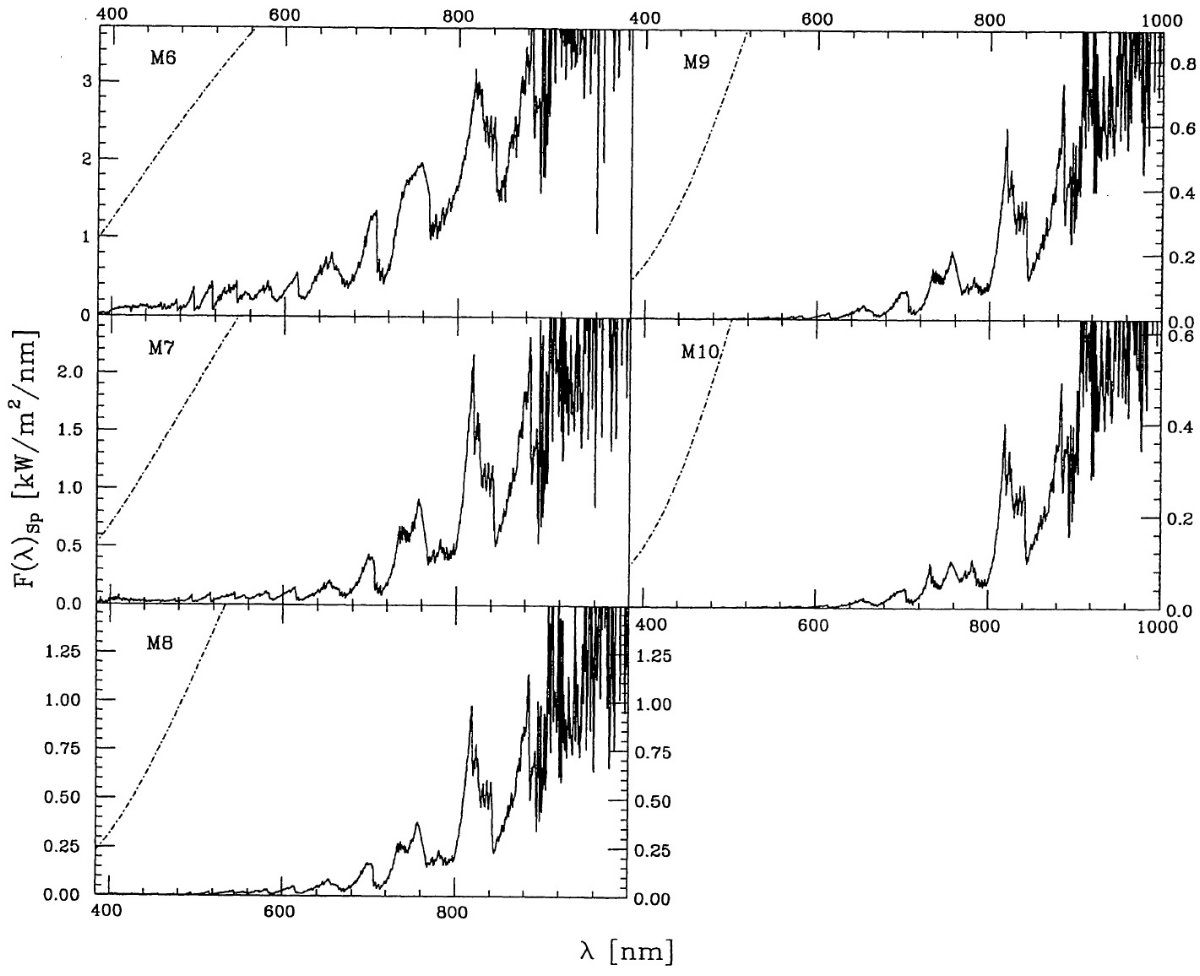
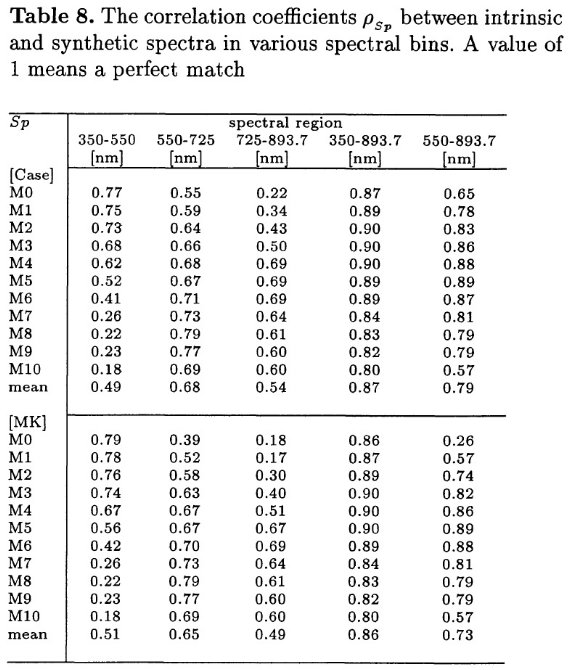 表8.固有スペクトルと合成スペクトルの間の相関計数. 1 = 完全フィット。 |
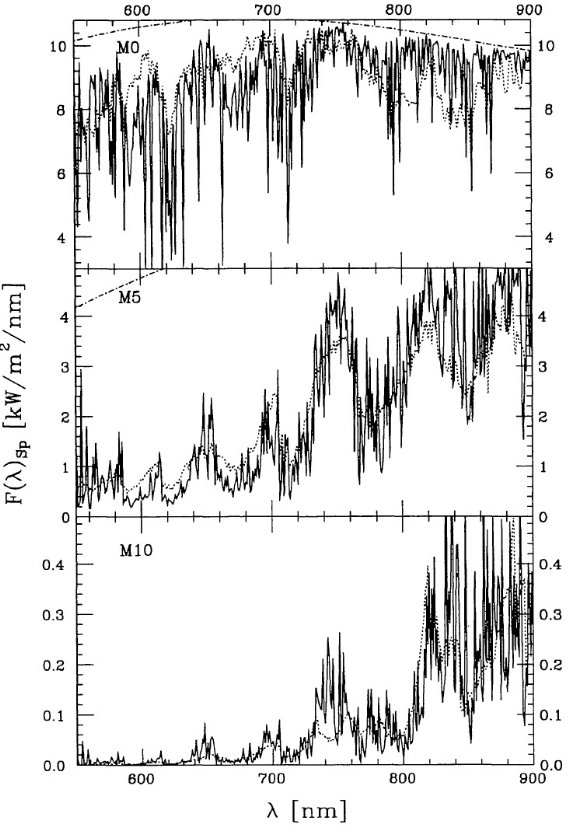 図8.点線= 固有スペクトル。実線=合成スペクトル。 上= MK 分類 M0, 中= Case 分類 M5, 下= Case/MK 分類 M10. 一点鎖線=連続光スペクトル。 |
|
Case 分類の原理 Case 分類は λ = [680, 880] nm 内の吸収帯に基づいている。 そこで、図9にはこの区間内で得られる全ての規格化スペクトルの積を 示す。図を見るとスペクトル積に3つの強い吸収帯があることが判る。 バンド1=[706, 724] nm, バンド2=[770, 807] nm, バンド3=[829, 857] nm のスペクトルエネルギー分布は M-巨星のスペクトルタイプに有用な 情報を与えてくれる。 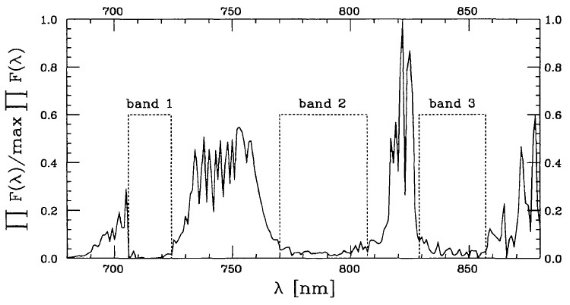 図9.分類区間内の全ての規格化フラックス( max で割るの意味?)の積 |
スペクトル指数
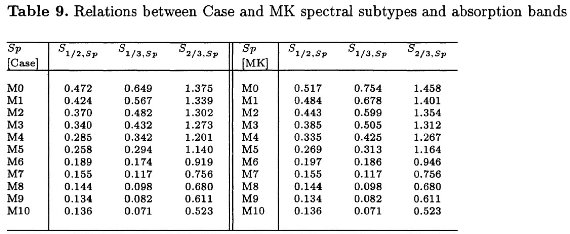 表9.Case と MK スペクトルにおけるサブタイプと吸収帯の関係。 |
|
エラー 図4の平均相対エラーは吸収帯の付近と 450 nm より短波長側で大きい。 前者は吸収スペクトルが星毎の温度、組成の差で変化することが原因である。 後者は短波長では露出不足となることが原因である。 1650 nm のコブ 図3と図6には 1650 nm のコブが目立つ。これは H- 吸収係数 の極小に対応する。この波長域は大気深くが見えるので Bell et al 1976 は 対流層を探るのに有用であるとした。コブの変化には次の特徴がある。 (1)有効温度が下がるとピーク位置が 1650 nm の方に動き、ピークが強まる。(?) (2)H2O ライン吸収がピークをブラケットし、それが有効温度の低下と共に 強まって行く。 (3)重力が弱くなるとピークが強まる。 ラインブランケッティング 固有スペクトル型が晩期に進むにつれ、ラインブランケッティングが 強くなってくる。表7の第5列にある MK スペクトル型に付けた有効温度と Ridgway et al. (1980) の有効温度とは MK M2 - M6 では一致する。我々のスペクトル分類はモデルと 独立になされているので、それと統計的計算(?)との一致が相互に矛盾しない ことを物語っている。M6 より先では Ridgway 温度との一致が悪い。これは 我々のモデルで使ったブランケッティングが不正確であるか、Ridgway たちの 光度決定に系統的なエラーがあるかのどちらかであろう。 |
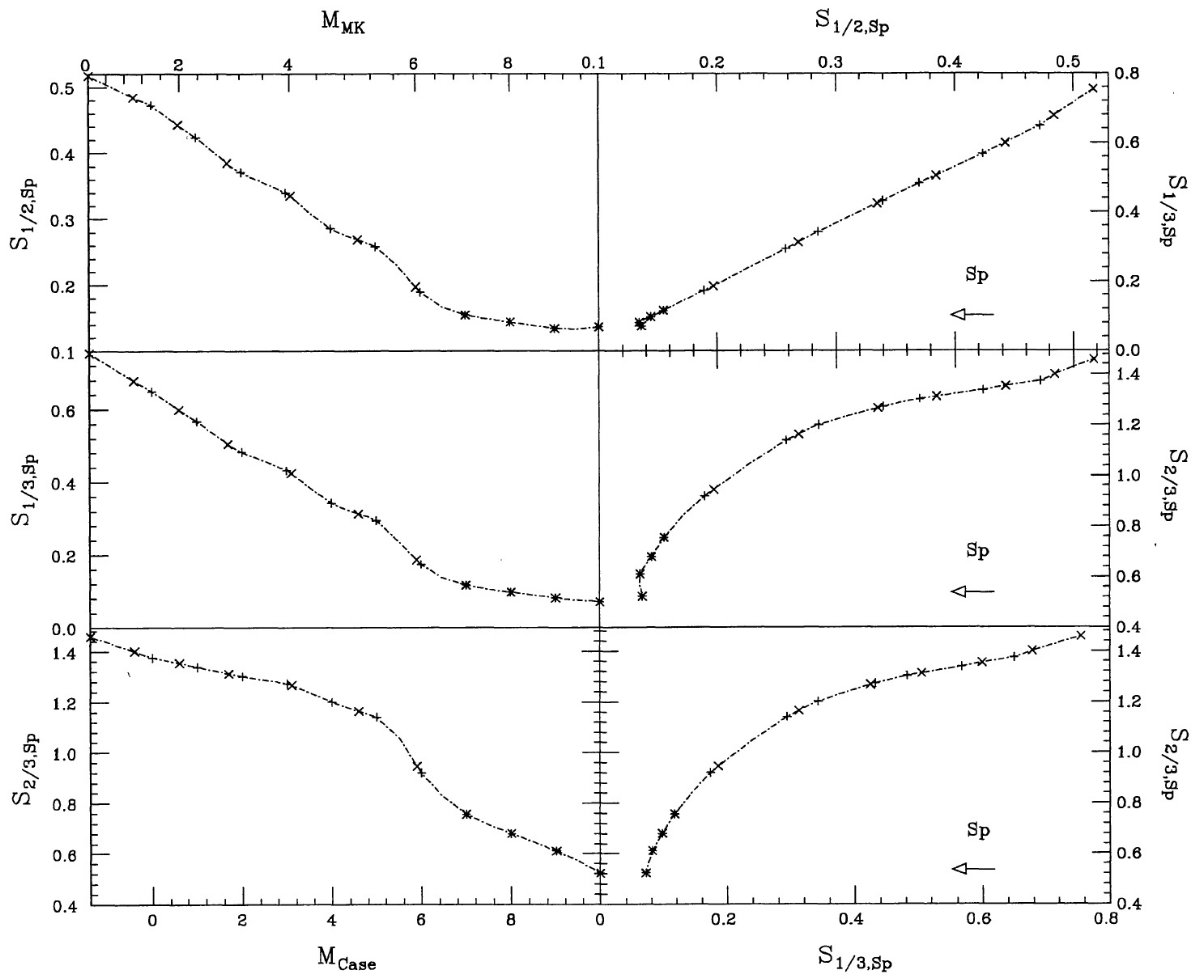
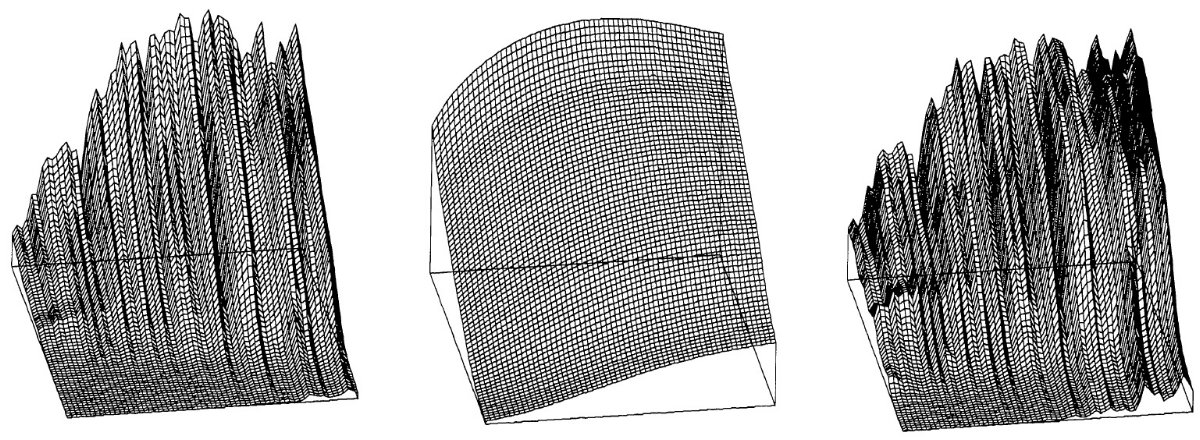
スペクトルをプロットすると、 Case と MK 分類の差が明らかになる。 Case 分類はスペクトルの赤波長にある吸収帯を用いている。一方、 MK 分類は青波長域の吸収線を用いる。 Case と MK の違い Case 分類は赤波長の吸収帯に、MK は青い波長帯を用いる。スペクトル型 が進むと、M-型巨星の青波長吸収の強度は赤波長側よりも急激に増大する。 MK 早期 M 型スペクトルは Case スペクトルほど急な変化は示さない。Case 中間スペクトル型は MK よりもゆっくり進む。その結果 M7 より後期では Case と MK は同じサブタイプとなる。これは図10での + と x 印の離れ 方に現れている。 図11=3次元表示 細かい特徴の違いを見よ。データは CDS から取得可能である。 |
|
|
|

|
|
|

|
|
|

|
|
|
