|
正常で主系列に近い B-, 晩期 O-型星から 328 個の IR - UV 減光曲線を得た。赤化ゼロ
SED を大気モデルで与えるという方法で減光を得た。この方法だと、スペクト
ルミスマッチによるエラーをなくすことが出来る。その結果、 1.2175 A コブの中心波長は小さい、幅は大きい変動を示す。相関はない。 2.UV と IR の減光特性間に強い相関がある。 3.Rvが極端な場合を除き、UV と IR 減光曲線間に相関はない。 |
4.視線方向間の大きな変動は、平均減光曲線は導く際のサンプルバイアス。 5.平均減光曲線で脱赤化すると大きな誤差を生む。 視線方向毎に減光曲線の変化が大きく、また曲線の特徴の間に相関が欠けて いるので、「平均減光曲線」を定義するのは困難である。減光曲線は局所的な 条件に敏感に反応するようである。つまり、各減光曲線は視線方向毎のグレインの 情報を含んでいる。 |
|
標準星抜き法の利点 1.赤化ゼロ標準星を観測する必要がない。 2.スペクトル型ミスマッチの影響をかなり減らせる。 3.赤化が弱い星の減光を以前より正確に決められる。 4.以前より低温度の晩期 B-型星まで使える。 5.減光曲線間の特徴の相関を定量的に扱える。 |
標準星抜き法の限界 固有スペクトルが大気モデルで十分に良く再現できなければならないので、 高光度星、 Be 星、WR-星、特異スペクトルの星全ては扱えない。しかし、この 制限はペア法でも同様である。 328 個のサンプル星 この論文では、多波長データが揃っている 328 個の星に対して、我々の標準星 抜き法を適用して、減光曲線を定める。研究の焦点は、 1.巾の広い結果を示す。 2.一般減光曲線を丁寧に調べる。 |

|
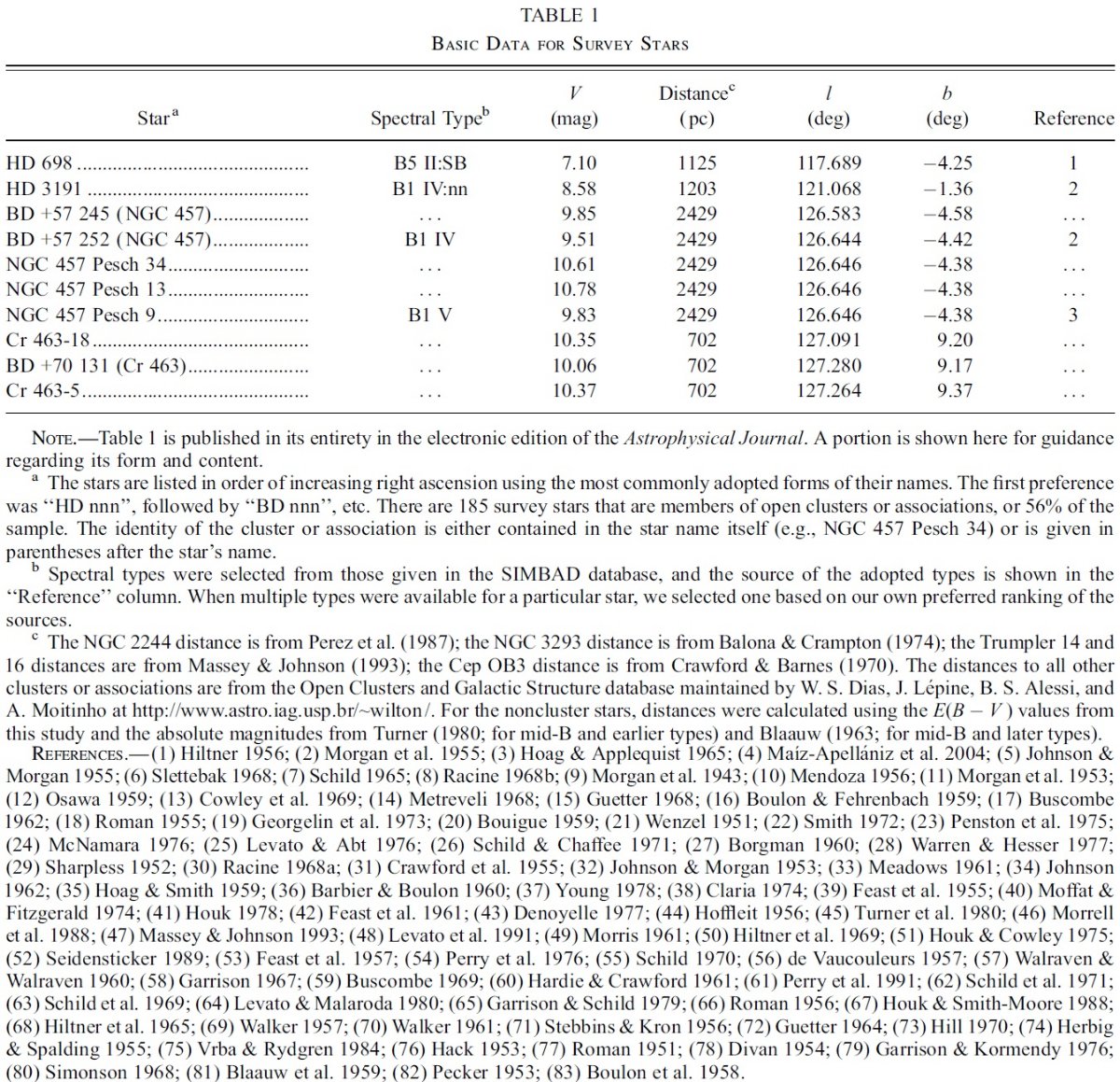
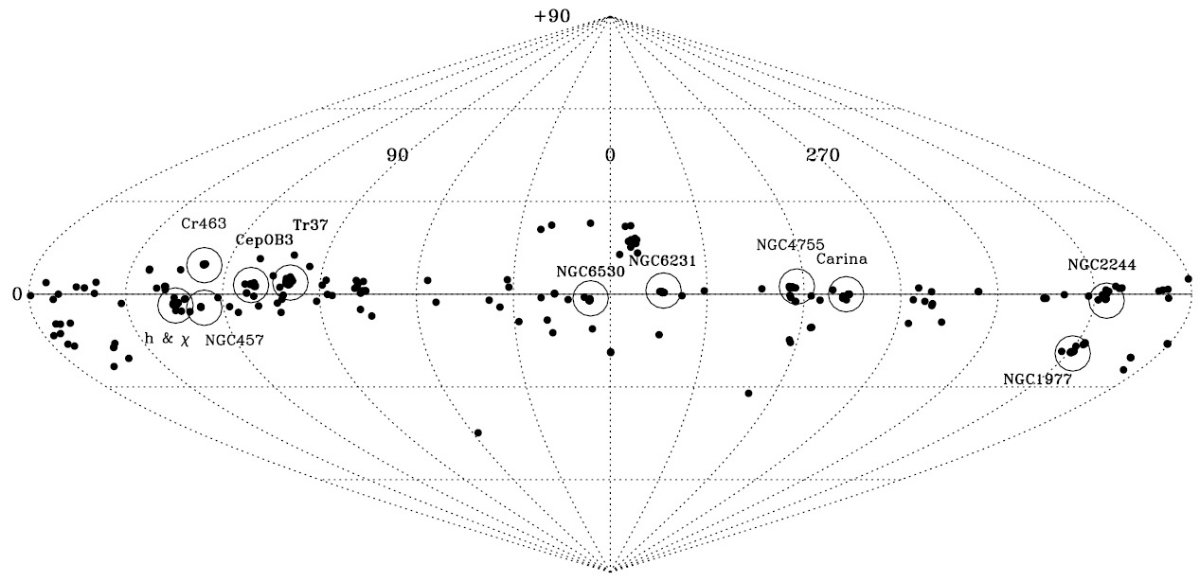
標準星抜き法の実際の応用 標準星抜き法の実際の応用は IUE 低分散スペクトルと UBVJHK 測光に 対して行われた。ストレームグレン ubvyβ 測光などは今回は使わない ので、 Fitzpatrick, Massa (2005b) より物理パラメタ―の精度は少し落ちる。 サンプル星 IUE スペクトル 1150 - 3000 A と UBV 測光が揃った 328 星を選び出した。 その内 298 星は何らかの近赤外測光があり、 287 星は J, H, K 等級が得られ ていた。 280 個は 2MASS である。表1にはそれらのデータを載せてある。 その全体は電子版で入手可能である。185 星は星団またはアソシエイションに 所属している。スペクトル型は SIMBAD から採った。 本当はスペクトル型は要らない B-型のスペクトル型は文献により大きく変わる。注意したいが、我々の解析 ではスペクトル型の知識は必要ではない。O-型星のスペクトルは一様で信頼の できる分類がなされている。その情報は解析に用いられた。 サンプル星の分布 図1はサンプル星が銀河面に集中していることを示す。それは我々が E(B-V) ≥ 0.20 という選択制限を設けたことの必然的な結果である。図2には解析 結果をグラフにまとめてあるが、サンプル星の性質を見るには便利である。 サンプル星の大部分は Teff = [15,000, 30,000] K の中間 B-型星でその赤化 中間値は E(B-V) = 0.45 である。 Rv の中間値は 3.05 であり、希薄星間空間 に対応する値である。しかし、 IUE 観測のバイアスが当然あるのでこの値を 星間空間一般の平均的性質を示すと解釈してはいけない。 |
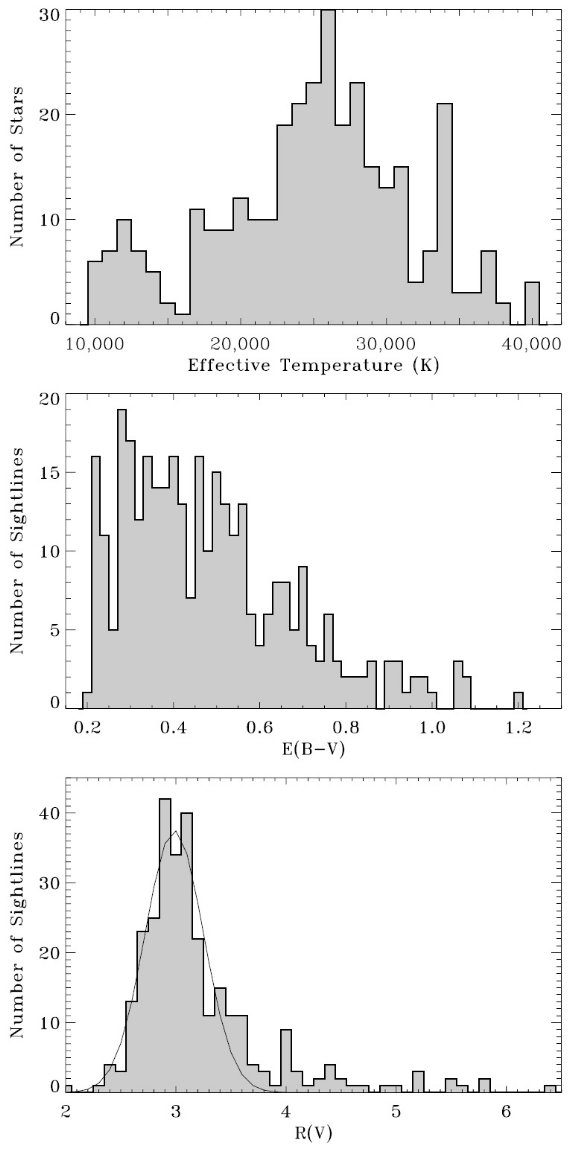 図2.サンプル星の性質の分布。上:典型的な星は中期 B-型星。中:赤化の 中間値は ⟨E(B-V)⟩ = 0.45. 下:希薄星間物質を通して見えている。ピーク位置は Rv = 2.99 で希薄星間 物質に付与されている値である。全体の平均と中間値は 3.22 と 3.05 である。 |
|
基本式 観測星の SED は以下の式で表現される。 fλ = Fλθ R210-0.4E(B-V)[k(λ-V)+Rv] (1) ここに、 Fλ = 恒星表面フラックス、θR = R/d = 星の視半径、k(λ-V) = E(λ-V)/E(B-V) は規格化減光曲線 である。この方程式を ATLAS9 大気モデルとパラメタ―表現された減光則により 最少二乗フィットする。 O-型星 今回は O-型星もサンプルに含んだ。その大気モデルは TLUSTY OSTAR2002 グリッドから採った。Teff = [27,500, 55,000] K の12ケース、Z/Zo = [0, 2], log g = [Eddington, 4.75], vturb = 10 km/s 固定が存在 するが、我々は太陽組成のみを扱った。なので、 TLUSTY モデルは実際には Teff と log g の2パラメタ―セットになる。O-型星の解析の結果、その IUE スペクトルは温度に影響されないため、我々の解析から決める温度は不定性が 大きいことが判った。そこで、O-型星の Teff に関してはスペクトル型から決めた Teff を採用することにした。表2に温度スケールを示す。 log g 広域測光データのみから決める log g の精度は一般に低い。だがしかし、星団の 星に関しては距離情報が使えるので、別である。 減光曲線紫外部 この論文の核心はパラメタ―化した減光曲線である。紫外部の表式は、 Fitzpatrick, Massa 1990 で次のように与えた。 k(λ-V) = c1 + c2x + c3 D(x, xo, γ) (x ≤ c5) = c1 + c2x + c3 D(x, xo, γ) + c5(x-c5)2 (x > c5) Fitzpatrick, Massa 1990 では c5 = 5.9 (1/μm) に固定されていたが、 ここではこの値もパラメタ―としてフィットを向上させた。2175 A コブは次の式で 表される。
これら全てで結局7つのパラメタ―を必要とする。 可視・近赤外域 スペライン内挿は IDL の SPLINE により行った。9つの錨点の内、紫外の U1, U2 は実際には IUE スペクトルの上の点であり、 k(B-V)=1, k(V-V)=0 の制限が付くので、フリーパラメタ―の数は 9 - 4 = 5 で ある。近赤外域 λ-1 = 0.0, 0.25, 0.50, 0.75, 1.0 μm ,sup>-1 の I1, I2, I3, I4, I5 では、以下の形を仮定する。 k(λ-V) = kIRλ べき乗指数もパラメタ―と考えることも可能だが、データ数が不足なので、 Martin, Whittet 1990 を採用した。 スプライン近似の理由 スプライン近似を使う理由は、単にこの波長域で尤もらしい解析的表現が存在 しないからである。今回の研究では可視域に (V, B-V, U-B) の3錨点しか使わない が、将来測光データが増加してもスプライン近似なら柔軟な対応が可能である。 |
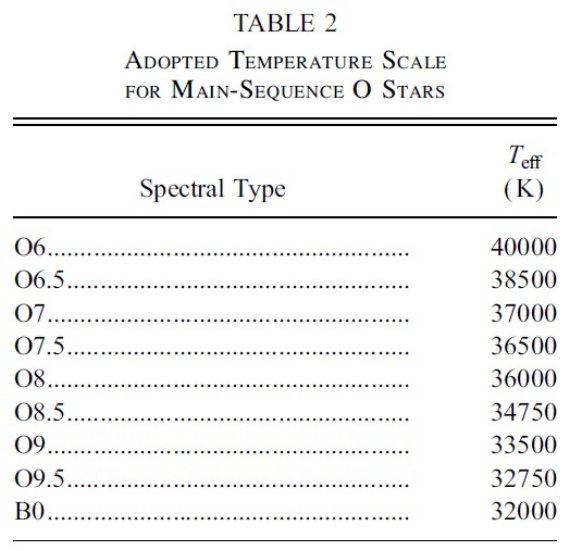 表2.O-型主系列星の温度 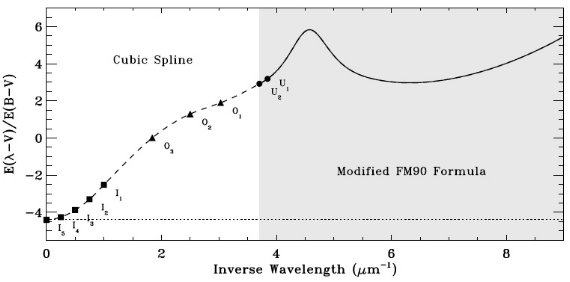 図3.規格化減光曲線 k(λ-V) のパラメタ―化した表現。斜線部= (λ≤2700A) 3成分パラメタ―表現。破線= (λ>2700A) で 赤外(In), 可視(On), 紫外(Un) の錨点をスプラインで内挿する。錨点の値と紫外部減光を決める7パラメタ― は観測 SED のフィットから決まる。 まとめると 328 赤化星の SED を式(1)により解析した。ベストフィットモデルを求 めるために、18パラメタ―を含むモデルを使用した。それらは、 大気モデルの (Teff, log g, [M/H], vturb), 減光曲線を指定する [O1, O2, O3, Rv, kIR, c1, c2, c3, c4, c5, xo, γ], 角半径 θR, E(B-V) である。 |

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|

|
|
|
