The Relationship between Infrared, Optical, and Ultraviolet Extinction

　1.イントロ　

　２．観測データと減光量の決定　

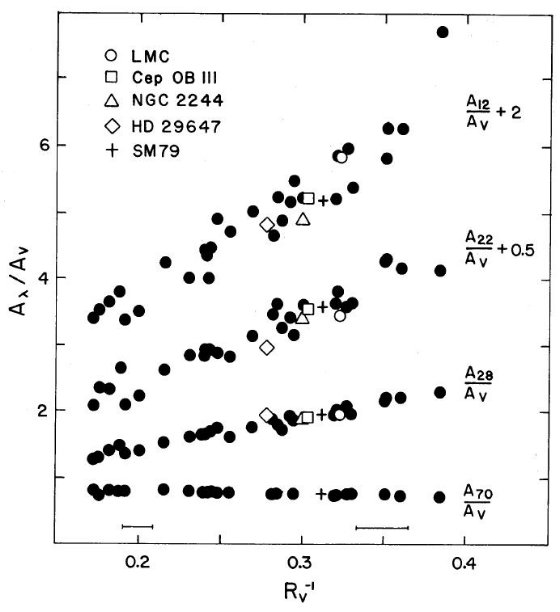
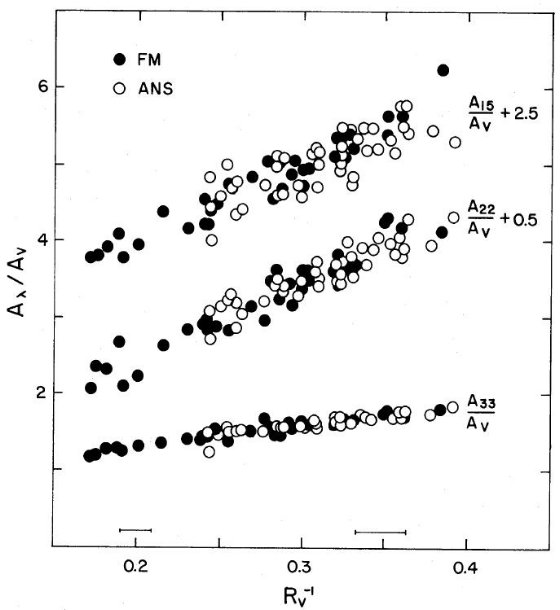
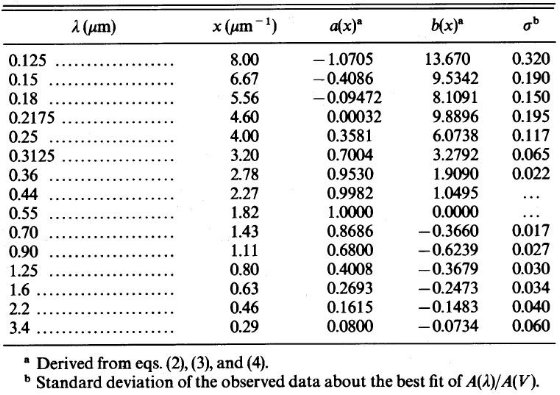
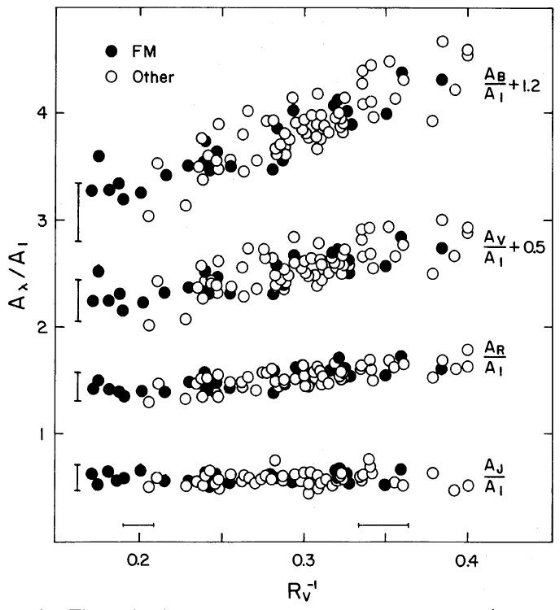
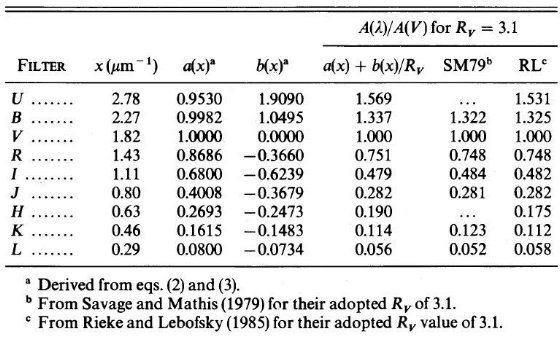
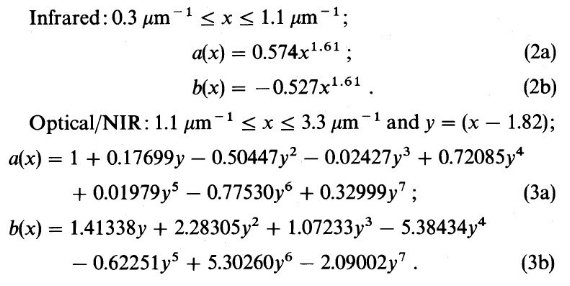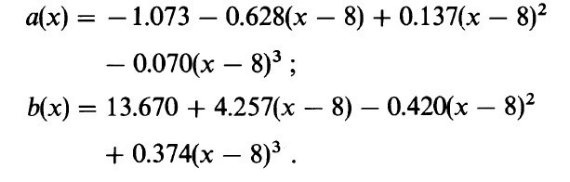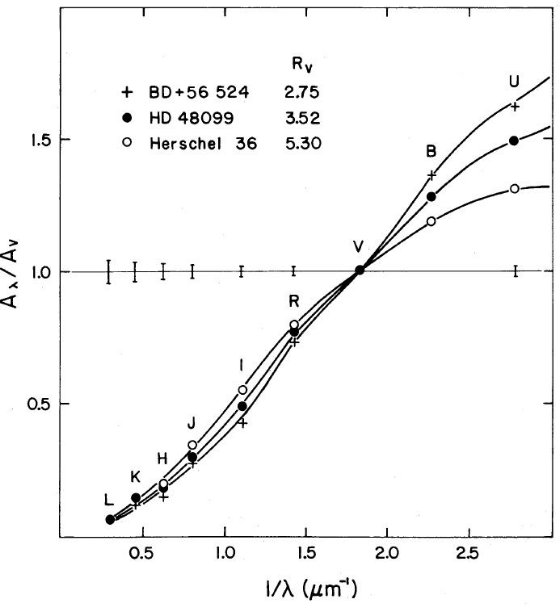
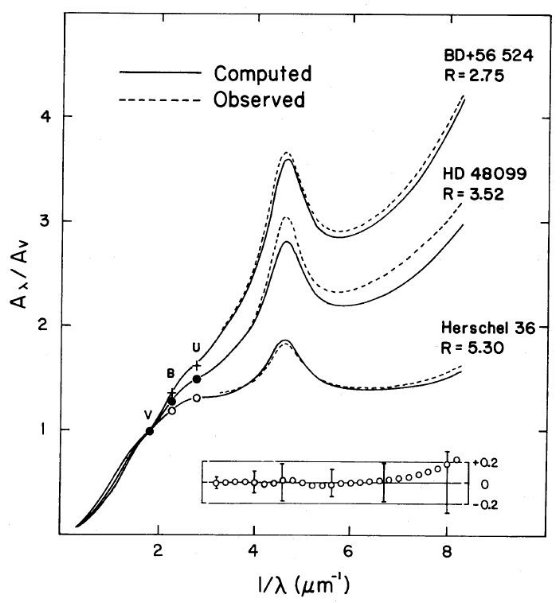
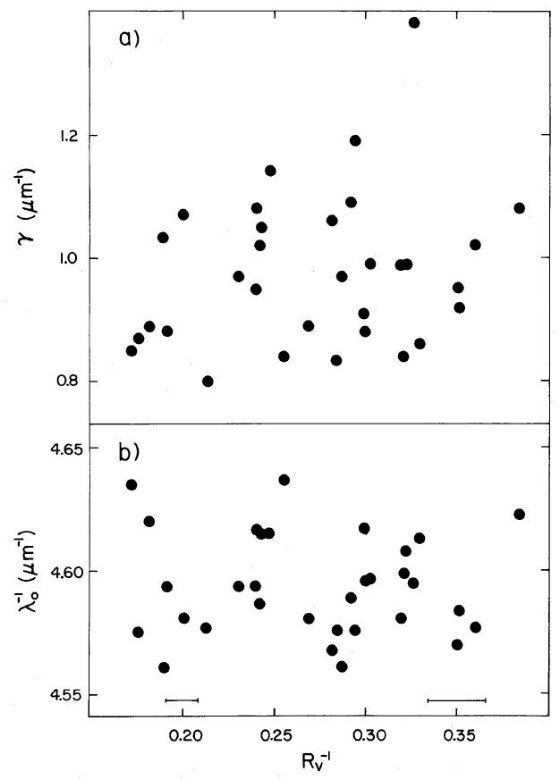
サンプル　 　FM 88 から多波長データのある星を選んで表１に載せた。その多くは U, B, V, R, I, J, H, K, L の観測がある。スペクトルタイプは FP 88 から 取ったが、元文献はそちらを見よ。固有カラーは Johnson 1966 を 使用した。これらの星のデータから、 (a). A(V) の決定 (b). A(V) と E(λ-V) から A(λ) と Rv = Av/E(B-V) (c). 減光曲線の特徴の比較　 　Av を決める第１の方法　 　λ > 0.55 μm では減光則は R = 3.08 の Rieke, Lebofsky 1985 に従う。この関数 A(λ)/A(V) = fRL(λ) と名付ける。k-番目の星の可視減光 Ak(V) は次の量を最少 にするように決める。 　　　　　χ2 = Σi[Ek (λi-V) - Ak(V)fRL (λi)]2 ここに i = R, I, J, H, K, L などである。Ak(V) が決まると、 観測された色超過 Ek(λi-V) から他の 波長の Ak(λi) が決まる。こうして Ak(λi)/Ak(V) が決まる。 ( χ2の式はおかしくないか？fRL(λ) を [fRL(λ)-1] で置き換える？) Ak(λi=Ak(V) + Ek(λi-V) は長波長側では引き算に 測定誤差の影響が大きくなる。Ak(V) ∼ -Ek(λi-V) で大引く大の計算。 Av の決定に fRL(λ) を使っているのだから、 Ak(λi=Ak(V) fRL(λ) とした方がよくないか？ 　Av を決める第２の方法　 　二つのカーブ、C fRL(λ) と Ak(V) + Ek(λ-V)、ここに C と Ak(V) は定数、 をくらべ、λ > 1.25 μm で一致するよう２定数を変えていく。 我々は減光曲線の形はこの波長帯では Rv に独立と仮定する。 この方法は実際の減光則は λ > 1.25 μm でのみ RL 型 と考え、 fRL(λ) は減光曲線を波長無限大まで外挿 するためのガイドとしてのみ使用する。 　両者の結果　 　我々のサンプルで計算した結果、双方から出した Rv は 5 % の精度 で一致していた。ただ、 Rv > 4.5 の 6 天体ではそうでなかった。 これらでは標準曲線からの逸脱が特に V で大きかった。さらに、その ３つ、θ1Ori C, θ1Ori D, Herschel 36、には明らかに λ > H バンドでの放射光の混入が見られる。 これらのケースでは第２法は R, I, J バンドのみに適用された。 表１に得られた値を載せた。

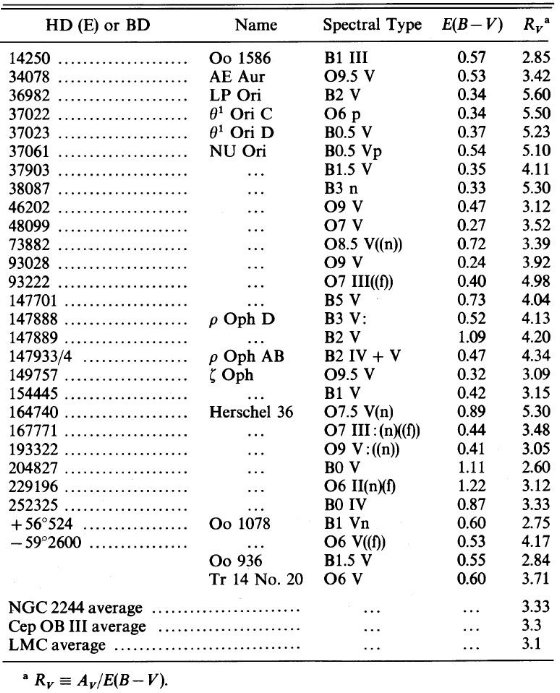
表１．観測データ

　３．観測的関係　

図１．（a）：A(λ)/Av と Rv-1=E(B-V)/Av の関係を Fitzpatrick, Massa 1988 サンプルにつき、いくつかの選択波長で示した。 ここで、例えば A12 は A(0.12μm) の意味である。 0.12μm と 0.22μm データは見やすさのため上方にずらした。エラーバー は Rv の二つの値における不定性である。白印は LMC と FM サンプル中の 二つの星団の平均値である。HD29647 データは Cardelli, Savage 1988 から採った。＋印は Savage, Mathis 1979 の平均曲線に対する値である。 0.12 μm は例外であるが、 Savage, Mathis 1979 の平均曲線は A(λ)/Av 対 Rv-1 関係の平均になっているように見える。 　３．a. A(λ)/Av と Rv の関係　 　A(λ)/Av と Rv-1 の 線形な関係が I バンドでも成立　 　 Cardelli, Clayton, Mathis 1988 (CCM) は 0.32 μm > λ > 0.12 μm において A(λ)/Av と Rv の関係を 調べた。彼らの結果は、x = 1/λ(μm) として 　　　　　A(λ)/Av = a(x) + b(x)/Rv 類似の関係は 可視 - 近赤外においても成立する。後に示す式 (2) - (4) は a(x), b(x) のよい近似式になっている。 　図１にその例を示す　 　図１左には 0.12μm, 0.22μm, 0.28μm, 0.70μm での A(λ)/Av 対 Rv-1 関係を示した。どの波長でも 良い線形性が認められる。Av の平均エラーは 0.05 Rv である。この エラーは図の下辺付近で二つ例示した。図１右は 0.15μm, 0.22μm, 0.33μm での同じ図である。白丸は ANS 減光超過カタログ (Savage et al 1985) から銀河面の様々の方向 を選んだ。減光/スペクトル型条件はデータ選択に適用しなかった。 　スペクトル型による除去　 　Savage et al 1985 では 減光/スペクトル型条件がデータ選択に適用され B8 より晩期の星が除去された。それらの多くは超巨星で固有カラーが Fitzpatrick, Massa サンプルに比べ不確定であるというのがその理由で あった。その上、 ANS 星のスペクトル型は UV データから直接決められた 分けではなく、その点 IUE スペクトルを用いた Fitzpatrick, Massa 1986, 1988 データとは異なる。それにも拘らず、 ANS データは Fitzpatrick, Massa データとよくフィットすることが図からわかる。 これは Fitzpatrick, Massa データが Rv 依存性の無バイアス表現に なっている表れと考える。

（b）：左と同じだが、データを追加した。黒丸＝Fitzpatrick, Massa サンプル。 白印＝ Savage et al 1985 の ANS 減光超過カタログから 可視 - 近赤外 データのある星を選んだ。0.15μm と 0.22μm データは見やすさのため 上方にずらした。 ( だから、右図の 0.22μm 黒丸は左図黒丸と同じ。) 表２．直線フィットの係数とフィットの偏差 　線形関係からのはずれ　 　図１に見えるように、各波長で線形関係からのはずれが見られる。はずれに R 依存は認められないので、波長ごとに標準偏差を作って表２に示した。 0.12 μm での偏差が他より大きい。

A(λ)/A(V) はよい規格化か？　 　図１を見ると、λ < V では A(λ)/A(V) は確かに Rv と共に 変化している。問題はもっと長波長側で、そこでの変化は規格化に A(V) を 選んだための効果ではないだろうか？ つまり、ある波長 λo が存在して、λ > λo では A(λ)/A(λo) は常に同じ関数になるのではないだろうか？規格化 には、そのような波長のうちで最も短いものが最善の選択である。 　A(I) による規格化　 　図２には λ = 0.44(B), 0.55(V), 0.70(R), 1.25(J) μm について A(λ)/A(I) と Rv-1 との関係を示した。点の分散は図１より 悪い。これは、A(I) が A(B) より小さく、測定誤差の影響が大きいためと思わ れる。規格化の特徴は A(V) での場合と似ていて、規格化波長より短い側では Rv-1 と共に増加していく。 　長波長側では単一減光則？　 　一方、興味深いことに、λ = 1.25 μm では勾配がほぼゼロとなる。データの分散は悪くなるが、同じ 傾向は H, K, L バンド全てで見られる。これは、以前から Jones, Hyland 1980, Koornneef 1983, Rieke,Lebofsky 1985, Smith 1987, Whittet 1989 が 述べていた、λ > 0.90 μm では単一減光則という主張と一致する 結果である。 　A(λ)/A(I) と A(λ)/A(V)　 　ではどこから単一減光則に移行するのだろうか？ 0.7 μm と 0.9 μm の 間らしいが、観測波長の間隔の問題で確定していない。Elias, Frogel, Humphreys 1985 による長波長減光は、さまざまな Rv の星に対するものだが、 Rieke, Lebofsky 1985 に完全に一致する。減光則が E(J-H)/E(H-K) のような色超過の比で表されている 場合には結果の間に少し差が生じている。ただ、その原因は究明しない。 　A(λ)/A(V) は Rv による作為的な変化を生み出すので好ましくない のだが、一方 A(λ)/A(I) はデータの分散が大きいという欠陥がある。 天秤にかけると、また歴史的ないきさつからもまだ広くは用いられていない。 　図２に使われたサンプル　 　図２の黒印は Fitzpatrick, Massa 1988 サンプル中 R, I, J データが存在するものである。白印はその他の 文献から集めた。これら 70 星は明らかに FM サンプルが減光則の平均的な Rv 依存性を表現していることを確認している。

図２．可視・近赤外波長域における A(λ)/A(I) と Rv-1 の関係。λ(I) = 0.90 μm である。B, V, R, J の波長は Johnson システムの値（表３参照）である。黒丸＝ FM サンプル。白丸＝他の視線方向 で可視・近赤外データのある星。B, V データは見易さのため縦にずらした。 Rv への依存度は λ > I で小さいため、Av で規格化した 図１と比べると、この図で採用した A(I) による規格化の方が良いようだ。

３．b. パラメタ―化： Rv 依存平均減光曲線　 　⟨A(λ)/A(V)⟩ = a(x) + b(x)/Rv 導出　 　可視・近赤外データのある FM サンプルを用いて、平均減光曲線 ⟨A(λ)/A(V)⟩ を 0.3 μm-1 - 3.3 μm-1 に拡大した。ちなみに、 　 Cardelli, Clayton, Mathis 1988 (CCM) のフィット範囲は、 3.2 μm-1 - 8 μm-1 である。解析法は CCM と同じで、A(λi)/A(V) を Rv-1 に対してプロットして、直線フィットの係数 ai, bi を求めるのである。こうして求めた a(xi=λ-1), b(xi) を x の多項式 として表す。すると、平均減光曲線は、 　　　　　⟨A(λ)/A(V)⟩ = a(x) + b(x)/Rv と表される。 　a(x), b(x) の多項式表示　 　計算上の理由で a(x), b(x) の多項式表示は３領域に分けて行った。 　可視・赤外部の表示　 表３．減光曲線の係数

図３では上式による減光曲線を３つの Rv が異なる星の減光観測と比較した。 モデル式が観測と極めて良い一致を示すことが分かる。λ ≥ 0.9 μm では A(λ)/A(I) は Rv には依らないらしいので、 x ≤ 1.1 の減光曲線は Rieke, Lebofsky 1985 と同じ A(λ) ∝ λ-1.61 則を適用している。 (だから、I で曲線が折れ曲がってる ) 　x = 1.1 - 3.3 μm-1 での近似は 7 次多項式で行った。 (　フィット点の数より次数が高い？ ) 　標準減光曲線との比較　 　表３には Rv = 3.1 に対する A(λ)/A(V) と、 Savage, Mathis 1979, Rieke, Lebofsky 1985 の平均減光曲線が載せてある。この表を見ると 満足のいく一致が得られていることが分かる。 　可視減光曲線の細かい構造　 　Whitford 1958 の減光曲線は最近 Ardeberg, Virdefors 1982 により 再確認されたが、 x = 2.25 で合わさる二本の直線から成る。我々の曲線は 広帯域バンドの観測に基づいており、減光曲線内の折れ曲がりのような 特徴はうまく表せない。我々の表式の優れた点は UV 減光曲線にスムーズに つながり、異なる Rv を持つ視線方向の減光曲線を統一的に表せる点に ある。 図３．異なる Rv の視線方向の観測減光曲線と、実線＝各 Rv に対応する A(λ)/A(V) = a(λ-1) + b(λ-1)/Rv.

紫外部の表示　 　図４には 0.3 μm-1 ≤ x ≤ 8 μm-1 の範囲で、モデルと観測とを比較している。HD 48099 は一致が最も悪い 星のひとつなので図に載せた。 標準減光曲線と比べるため、図４下の枠内に Seaton 1979 の標準 紫外減光曲線と Rv = 3.2 モデルとの差を示した。x ≤ 7 では 差は ± 4% である。しかし、x ≥ 6.7 では差が次第に 大きくなっていく。ただ、 Seaton 1979 は Rv が不明ないくつかの 減光の平均値から作られている点に注意が必要である。 　極紫外　 　x ≈ 8.3 で、 A(0.12μm)/A(V) は図１に示してある。 　この式は x = 8 - 10 で FM 1988 を 外挿したものである。

図４．波長域が違うが他は図３と同じ。下の枠内は Seaton 1979 の標準 紫外減光曲線と Rv = 3.2 モデルとの差。

３．c. 紫外と可視・近赤外の減光パラメタ―の関係　 　FM88 式の変形　 　 Fitzpatrick, Massa 1988 (FM88) は個々の星の紫外減光曲線を３つの関数の重ね合わせで表現した。 式で書くと、 　　　　　FM(x) = E(λ-V)/E(B-V) 　　　　　　　　= c1 + c2x + c3 D(γ,xo) + c4P(x) ここに、D(γ,xo) はドルーデ関数、γ はコブの FWHM、xo は コブの中心 x、P(x) = x3 (x > 5.9) は反り返りを 表す。我々は減光を A(λ)/A(V) の形で考えているので、 その形に直すと、 　　　　　A(λ)/A(V)=[FM(x)E(B-V)/A(V)]+1=[FM(x)/Rv]+1 図７．バンプ強度/Av と Rv の関係。黒丸は FM88 サンプル。白丸 は ANS サンプル。Rv 依存性は明らか。

コブの強さ　 Abump = コブの強さを線形背景減光の引いた分と考えると、 　　　　　Abump/A(V) = c3/(γ2Rv) である。図７に、Abump/A(V) と Rv-1 との関係を 示す。 　ANS データから観測的に決めた Abump は、 E(22-V) - E(15-V)/2 -0.62E(B-V) である。この式は、ANS 観測のある FM88 データとの比較から経験的に得られた。図８にはこうして得た Abump/E(B-V) と c3/γ2 からの Abump/E(B-V) が比べられている。 図８．バンプ強度/E(B-V) の比較。

図９．Abump/E(B-V) と Rv-1 との関係。データは 図７と同じ。図７と同じ情報なのに、こちらには相関は認められない。この 違いは、減光の解釈が規格化の方法、特にE(B-V)により大きな影響を受ける ことを示す。

図１０．(a): コブの FWHM γ と Rv-1 の関係。 (b): コブの中心波長 λo-1 と Rv-1 の関係。 図７に示したコブ強度/Av が Rv と相関したのに対し、こちらは相関がない。 これはコブの原因となる粒子は Rv の変化を生む粒子と違うことを示唆する。 Abump/Av が Rv-1 と相関する説明としては、 例えば、Rv が大きくなり粒子がくっつきあう際には コブを生み出す 粒子が取り込まれてコブを作れなくなるなどがある。

　４．議論