The birthrate of planetary nebulae

２．惑星状星雲の誕生率　

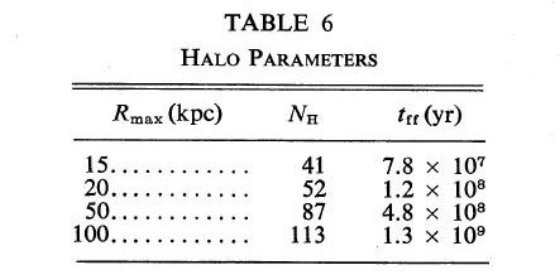
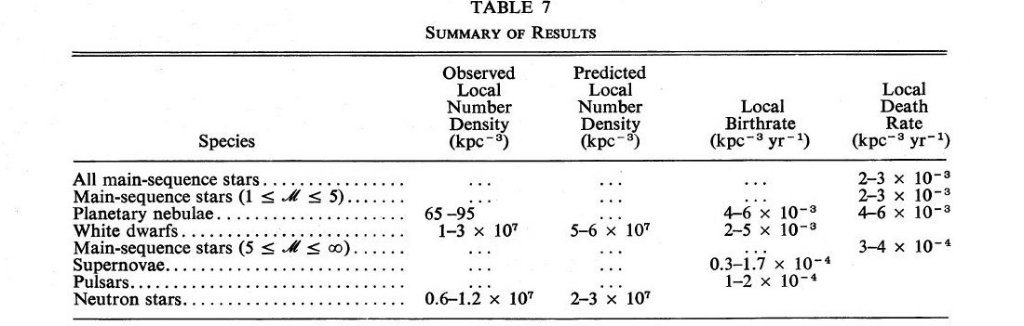
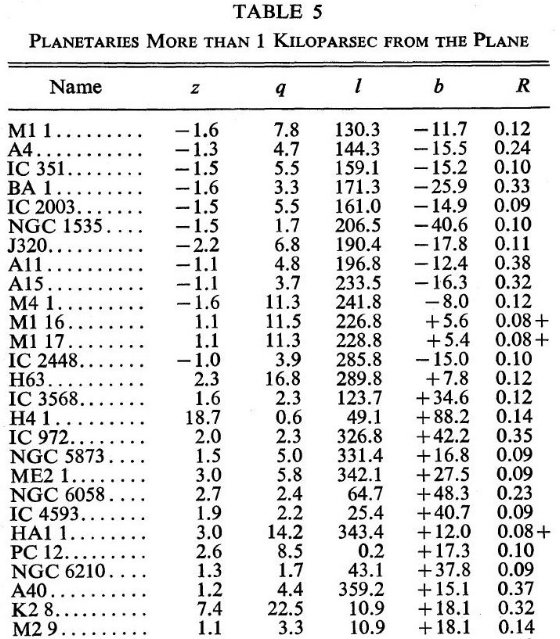
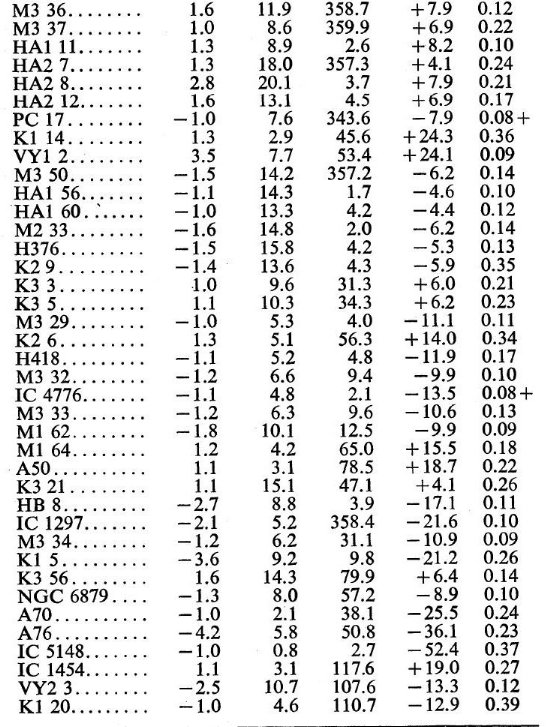
改訂距離に基づく近傍ＰＮサンプルの数密度　 　誕生率の推定に必要なのは数密度と寿命である。Cahn 1976 による新しい減光分布 (FitzGerald 1968 の３次元カラーエクセス分布を変換)を用いて、１９７１のＰＮ距離 決定を計算し直した。改訂距離は 1971 年版より 5 - 10 % 大きくなった。 　半径 R が、R1 ∼ 0.08 pc ≤ R ≤ R ∼ 0.40 pc の光学的に薄い星雲に対しては信頼できる距離が得られる。表１には半径がその範囲に あり、太陽から水平(lateral)距離 1.1 kpc 以内の 41 天体が挙げてある。水平距離とは 銀河面への投影距離である。この距離 1.1 kpc は検出率が急激に低下し始める距離であ る。表１の ∗ はパロマーサーベイで見つかったＰＮである。 南北非対称な分布　　 表１の４１天体中３０天体が北半球からであることは注意すべきである。これは ∗ 印のある、すなわちパロマーサーベイで見つかったＰＮが２１もあり、しかも その内２０は北半球天体であることが原因であろう。パロマーサーベイが全天の 75 % を カバーしていることを考慮すると、その領域にある 37 天体が完全であると考えて 37 × (4/3) = 49 個が本当の値と考えてよいだろう。または、南半球は減光が 強いのであると考えて、北半球の個数３０を倍にして６０天体と考えてもよい。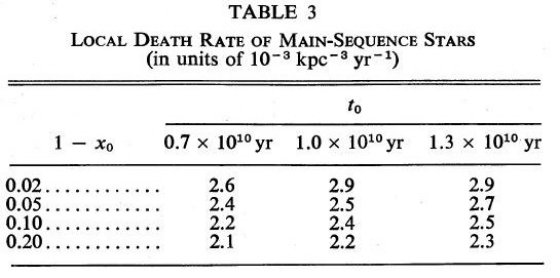 太陽近傍密度の導出　　 　表１をそのままで見たまとめが表２に載っている。第１行は円柱内のＰＮ数、第２行 は柱密度、第３行には銀河面から 50 pc 以内のＰＮ数が載っている。第４行は面から 50 pc 以内の数を使った局所密度、第５行は 80 pc 以内の数に基づく密度が載っている。 太陽からの平衡距離が 0.5 kpc 以内のＰＮ数が非常に小さいことと、遠くでは未検出 ＰＮ数が増えることを考えると局所密度として 60 ± 10 kpc-3 が 妥当である。でも、表からは太陽近くが落ち込んではいないけ ど。 この値は Cahn,Kaler 1971 の 50 kpc-3 と合致する。 　次に、表１の所で議論した南北格差を表２に即して考えよう。表１では記載の４１ 天体を 55 ± 5 天体へ変えた。表２でも同じ割合で変更すると、柱密度として 19 ± 2 kpc-2、 局所密度として 80 ± 15 kpc-3 が最終値となる。 Cudworth スケール　　 　この論文では距離決定に Seaton 1966 のスケールが用いられている。最近　Cudworth 1974 が統計視差に基づく新しい距離決定を提唱した。Cudworth の距離は Seaton のに 較べると 1.43 倍長いので、数密度は 1/3 倍に減る。したがって、このスケールでは PN 密度は 27 kpc-3 になる。どちらの距離尺度が良いか今後の研究が 決めるであろう。 ＰＮ誕生率　 　理想的には半径に依る膨張速度 V の変化が分かるとよいが、現在のデータではそこまで 行かない。そこで V = 20 km/s を仮定する。表１のサンプルが半径 R1 と R2 の間にあるＰＮであったから誕生率は、 χ = n0 v = (80 ± 15) kpc-3 × 20 km/s R2 - R1 (0.40 - 0.08) pc 　 　　　　　　　　　　　　　　　　　　= 5.1 ± 1.0 × 10-3 kpc-3 yr-1 　南北格差の補正を除けば、この値は Cahn, Kaler 1971 が出した誕生率、 3.2 × 10-3 kpc-3 yr-1 と大体同じである。 銀河全体でのＰＮ誕生率　 　今回、銀河全体でのＰＮ総数を評価する方法は 1971 論文とは異なる。 （１）　太陽近傍の柱密度 19 ± 2 kpc-2 に、半径 15 ± 3 kpc と仮定した銀河円盤面積を掛けて総数を出すと、13 ± 3 × 10 3 となる。式（１）に含まれているＰＮ寿命は 1.6 × 104 年なので、銀河系全体でのＰＮ誕生率は 1 yr-1 となる。 （２）　Schmidt 1963 によると、太陽近傍での柱密度は 75 M๏ pc-2 である。ＰＮが銀河系物質に均一に混ざっていると仮定すると、 銀河系質量として　1.5 × 1011 M๏ をとって、 PN 総数 = (19/75) × 106 × 1.5 × 1011 = 3.8 × 104 個となる。ＰＮ誕生率は 2.4 yr-1 である。 参考となる数字として、Alloin, Cruz-Gonzalez, Peinbert 1975 は 6000 - 30,000 個 という数字を挙げている。

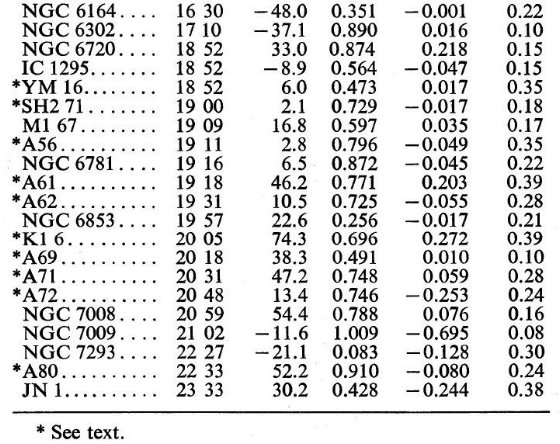
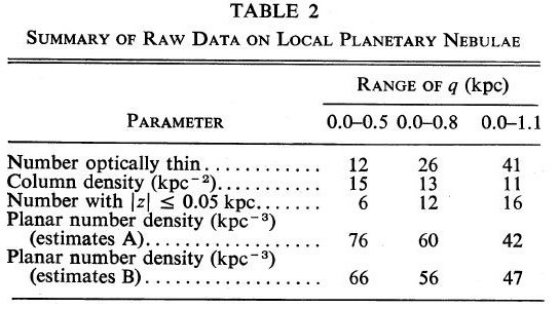
表１　南北半球での非対称性に注意 表２　表１の生データのまとめ

　３．主系列星の死亡率　

ここでは、ＰＮ誕生率をＭＳ死亡率と較べる。 太陽近傍の星形成史　 Mo = Ms + Mg = 1 kpc3 内の総質量で時間に関し一定とする。 Ms = Mo x とおく。Mg = Mo (1-x) となる。 星形成率を dMs/dt = A Mg と仮定する。A が星形成係数となる。Ms から　Mg へのリサイクルを無視すると、 dx = A ( 1 - x )　　　　　　　　　　(2) dt 　したがって、 　　　　　　　　 x = 1 - e-At　　　　　　　　　　　　 　　　　　(3) 星形成で集積した主系列星の数　 　次に、規格化した星の初期質量関数を g(M) とする。g(M)dM は、ガスから星に変 わる単位質量中 dM 内の星になる質量比である。 すると、時間 dt の間に dM 内の星に なる質量は、　A Mo g(M) dM e-At dt なので、星の数に直すには M で 割ればよい。 　　　　　　　　　A Mo [g(M)/M] dM e-At dt 　　　　　　　　　　(5) 　すると、現在つまり銀河年令経って後に主系列にいる M > 1 (太陽単位) の 星の数は、 φ(M, to) dM = A Mo g(M) dM ∫ to e-At dt M to - τ(MS) = Mo g(M) dM exp(-Ato)[exp(AτMS) -1] 　　(6) M 今、主系列から離れる星の数　 　今、主系列から離れる星は、 銀河系時間 t = to - τMS に形成されている。dM 内 にある星が主系列から単位時間に離れる数は、 t = to - τMS に 生まれた星の数であるので、式（５）から D(M, to)dM = A Mo g(M) dM exp [- A(to - τMS)] 　　(7) M 　こうして、質量 M (>1) の星に対して、現在の存在数と死亡率との比が次の式で 与えられる。 D(M, to) = A φ(M, to) 1 - exp (- A τMS) これだけだったら、今のガス量を１とすると、ｔ昔のガスは et なので、 　　　τ 昔の生成率 = A eAτ 　　　今の存在数 = A ∫0τeAt dt = eAτ - 1 両者を辺々で割れば上の式が出る。 表３．主系列星の死亡率(10-3 kpc-3 yr-1)

死亡率の計算　 　主系列星死亡率を出すため、以下のような数値を入力する。 (a) Schmidt 1959 の主系列光度関数 (b) Mv と Mbol の関係 (c) M - Mbol 関係 (d) 主系列寿命　τMS = 1010 M-3 年 　幾つかの銀河年令、現在のガス割合 (1 - xo)つまり色々な星形成率Ａ、に対し数値 計算を行った。表３はその結果である。主系列星の死亡率は、2 - 3 × 10 -3 kpc-3 yr-1 であることがわかる。 　表３の計算に入力した値はファクター 2 - 3 くらい狂うかも知れない。この点で Abell, Goldreich 1966 がスケール高度を 0.1 kpc として 1.2 M๏ 以上 の星の死亡率として、2 × 10-10 kpc-3 yr-1 を出しているのは参考になる。 どうして死亡率の値がこんなに安定しているんだろう？ D(to) = A Mo exp [- Ato] exp [ + A τmean] Mmean だが、合成ＨＲ図の主系列端は実際には t = to の星と考えると、τmean = to、で結局、 D(to) = A Mo / Mmean になってしまう。Ato = 3.91(xo = 0.02) , 1.61(xo = 0.2) に対応して、A=2/10Gyr=0.2 Gyr-1 = 2 × 10-10 yr-1　のファクター２くらい のあたり。柱密度 75 M๏ pc-2 の厚みを 0.2 kpc として、 Mo = 4 × 108 M๏ pc-3 程度となる。 さらにMmean = 1 M๏ を上の式に代入 すると、D(to) = 2 × 10-10 × 4 × 108 あれっ、一桁ちがう！ ∫(g(M)/M)exp(τMS)dM=Frac/Mmean で Frac < 0.1 くらいになるのかも知れない。Mmean も３くらいにすれば 何とかなるかも？ 　計算の副産物として、ある質量以上の星に対する死亡率も計算できる。表４では to = 10 Gyr, 1-xo = 0.05 の場合について、それらを載せた。 　第２列は次の式で定義される。 　　　　　　　　　I(M, to) = ∫M&inf;D(M,to)dM 　主系列星死亡率を惑星状星雲誕生率と比較する前に、超新星への下限質量を確定して おかなければならない。ここでは M = 5 をその値とする。表４によると、死んでいく星の 14 % が　質量５以上である。この割合は数値のエラーを考えると結果に影響する数字 ではない。 　表４　第１列の質量より重い星の主系列死亡率。(kpc-3 yr-1)

　４．白色矮星　

　５．ハロー惑星状星雲　

大質量ハロー　？　 　Ostriker, Peebles 1973 は銀河系円盤を安定化するには非常に重いハローが 必要であることを示した。もしそうであるなら、球状星団やハロー惑星状星雲 の分布と運動にそれが反映されているだろう。 ハロー惑星状星雲サンプル　 　表５には、Cahn, Kaler 1975 の改訂惑星状星雲カタログから採った、銀河面 高度 1 kpc 以上でかつ半径 = 0.08 - 0.4 pc の６６個の星雲が載っている。 平行距離 5 kpc 以下、面高度 5 kpc 以下だと見かけ半径は 2".3 以上となり、 Hβ フラックスは検出限界 10-12 ergs s-1 cm -2 以上となる。また、星間吸収も無視できる程度に弱い。したがって、検出 は平行距離 5 kpc までは完全と思われる。 円盤天体の汚染　 　|Z| < 5 kpc, q < 5 kpc の円柱内には 22 星雲がある。その内、|Z| ≥ 1 kpc は　22 天体、|Z| ≥ 2 kpc は　1.5 天体である。(0.5 は丁度 2 kpc 天体分) これらは、平均密度の 0.035 kpc-3 と　0.003 kpc-3 を それぞれ与える。もし、ハロー惑星状星雲が銀河中心の周りに球対称分布をしている なら、二つは似た値となるはずである。したがって、少なくとも |Z| = 1 - 2 kpc 領域は円盤天体が支配的であることを示す。|Z| = 2 - 5 kpc での平均密度　 0.003 kpc-3 の方がハローの密度に近いだろう。 サンプル数＝１．５はかなり問題。特にこれからハロー質量 を出すのは？ ハロー全体のＰＮ総数　 　球状星団の密度分布は ∼ R-3 (Arp 1965) なので、惑星状星雲 も同じ密度分布形を持つとすると、ハロー中の惑星状星雲の総数は、 NHalo = 4 π nHalo (Ro) ∫ Rmax Ro3 R2dR Rmin R3 = 4 π nHalo (Ro) Ro3 ln Rmax Rmin 　nHalo(Ro) = 0.003 kpc-3, Ro = 10 kpc, Rmin = 5 kpc で 固定し、Rmax を 15 kpc から 100 kpc まで変えての 計算結果は表６にまとめられている。冪乗指数を -2.5, -3.5 に変えて計算したが、 結果に大きな変化はなかった。 ハロー質量の推定（かなり無理してる）　 　ハロー質量の最大値推定にあたり、次の仮定を置く。 （１）ハロー天体は初期自由落下期に形成された。tff = (3π/32Gρo) 1/2 （２）ハローＰＮは最近の t = 0 から PN 寿命 tPN ∼ 16,000 年 の間に形成。 （３）ハローＰＮ母星は M ∼ 1 で、主系列絶対等級 Mv = 4.6 付近に集中する。 　　　第３章で引用した（？）関係は、 　　　　　　　　　Mv = 4.6 - 10.0 log M 　　　　　　　　　(12) 　　　これを、主系列寿命の式 　　　　　　　　　τMS = to M-3 　　　　　(13) 　　　と組み合わせると、 dτMS = tPN = - 3dM = 0.69 dMv　　　　　(14) τMS to M 　　　数値を入れると、dMv ∼ 2.3 × 10-6 である。 （４）ＩＭＦは時間依存がないとして、第３章の g(M)dM を数値的に用いる。する 　　　と、Mv = 4.1 - 5.1 (4.6 を中心に１等巾)内には質量比で全体の 1 % が 　　　入ることが分かる。したがって、現在のＰＮは全体の ∼ 2.3 × 10-8 　　　である。 （５）すると、ハロー天体の R = Ro 付近での密度は、 　　　nHalo(Ro) × 1M๏/2.3 × 10-8 ∼ 0.003 M๏ kpc-3/2.3 × 10-8 　　　　　　　　　　　　　　　　　　　　　　∼ 1 - 2 × 10-4 M๏ pc-3 （６）ハロー全体のＰＮ総数を表６から 40 - 110 と見て、ハロー質量は、 　　　[(40 - 110)/0.003] × (1 - 2) × 10-4+9M๏ ∼ (2 - 5) × 109M๏ （７）ハロー質量の評価は粗く、ハローＰＮ密度に入る円盤ＰＮの汚染が不確か 　　　なので上記の値は上限と見るべきだろう。 ハローは 1 - 3 % !　 　以上の考察から、ハロー質量は全銀河の 1 - 3 % を越えないという結論になる。この 結果は色々な仮定の上に成り立っていることは確かだが、他の独立な推定値が似た値を 出していることを注意する。例えば、 Weistrop 1975 は 6 × 10-4M๏ pc-3、 Schmidt 1975 は 1.7 × 10-4M๏ pc-3 という値を得ている。

表５．銀河面から 1 kpc 以上の高さにある惑星状星雲 表６．仮定したハロー半径によるＰＮ数の変化

　６．結論